A Practical Guide to Power Analyses of Moderation Effects in Multisite Individual and Cluster Randomized Trials

Figures & data

Figure 1. A conceptual framework for investigating moderation effects of professional development.

Note: This figure is a reproduction of Figure 1 from Dong et al. (2023a).

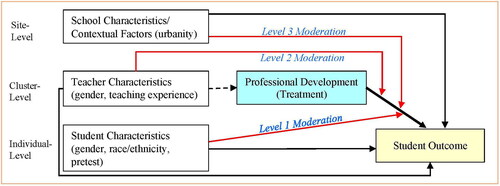
Table 1. Summary of statistical models for the moderation analysis in two-level MIRTs and three-level MCRTs.

Model number	Statistical model
MRT2-1R-1	L1: $Y_{\mathit{\text{ij}}}={\beta }_{0j}+{\beta }_{1j}{T}_{\mathit{\text{ij}}}+{\beta }_{2j}{T}_{\mathit{\text{ij}}}{M}_{\mathit{\text{ij}}}^{(1)}+{\beta }_{3j}{M}_{\mathit{\text{ij}}}^{(1)}+{\beta }_{4j}{X}_{\mathit{\text{ij}}}+r_{\mathit{\text{ij}}}$	$r_{\mathit{\text{ij}}}\sim N(0,{\sigma }_{|T,M,X}^2)$
	L2: ${\beta }_{0j}={\gamma }_{00}+u_{0j}$ ${\beta }_{1j}={\gamma }_{10}+u_{1j}$ ${\beta }_{2j}={\gamma }_{20}+u_{2j}$ ${\beta }_{3j}={\gamma }_{30}$ ${\beta }_{4j}={\gamma }_{40}$	$\left(\begin{array}{c}{u}_{0j}\\ u_{1j}\\ u_{2j}\end{array}\right)$∼$N\left[\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right),\left(\begin{array}{ccc}{\tau }_{00}^2& {\tau }_{01}^{}& {\tau }_{02}^{}\\ & {\tau }_{11}^2& {\tau }_{12}^{}\\ & & {\tau }_{22}^2\end{array}\right)\right]$
MRT2-1R-2	L1: $Y_{\mathit{\text{ij}}}={\beta }_{0j}+{\beta }_{1j}{T}_{\mathit{\text{ij}}}+{\beta }_{2j}{X}_{\mathit{\text{ij}}}+r_{\mathit{\text{ij}}}$	$r_{\mathit{\text{ij}}}\sim N(0,{\sigma }_{|T,M,X}^2)$
	L2: ${\beta }_{0j}={\gamma }_{00}+{\gamma }_{01}{M}_j^{\left(2\right)}+u_{0j}$ ${\beta }_{1j}={\gamma }_{10}+{\gamma }_{11}{M}_j^{\left(2\right)}+u_{1j}$ ${\beta }_{2j}={\gamma }_{20}$	$\left(\begin{array}{c}{u}_{0j}\\ u_{1j}\end{array}\right)$∼$N\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\tau }_{00|M}^2& {\tau }_{01|M}^{}\\ & {\tau }_{11|M}^2\end{array}\right)\right]$
MRT2-1N-1	L1: $Y_{\mathit{\text{ij}}}={\beta }_{0j}+{\beta }_{1j}{T}_{\mathit{\text{ij}}}+{\beta }_{2j}{T}_{\mathit{\text{ij}}}{M}_{\mathit{\text{ij}}}^{(1)}+{\beta }_{3j}{M}_{\mathit{\text{ij}}}^{(1)}+{\beta }_{4j}{X}_{\mathit{\text{ij}}}+r_{\mathit{\text{ij}}}$	$r_{\mathit{\text{ij}}}\sim N(0,{\sigma }_{|T,M,X}^2)$
	L2: ${\beta }_{0j}={\gamma }_{00}+u_{0j}$ ${\beta }_{1j}={\gamma }_{10}$ ${\beta }_{2j}={\gamma }_{20}$ ${\beta }_{3j}={\gamma }_{30}$ ${\beta }_{4j}={\gamma }_{40}$	$u_{0j}\sim N(0,{\tau }_{00}^2)$
MRT2-1N-2	L1: $Y_{\mathit{\text{ij}}}={\beta }_{0j}+{\beta }_{1j}{T}_{\mathit{\text{ij}}}+{\beta }_{2j}{X}_{\mathit{\text{ij}}}+r_{\mathit{\text{ij}}}$	$r_{\mathit{\text{ij}}}\sim N(0,{\sigma }_{|T,M,X}^2)$
	L2: ${\beta }_{0j}={\gamma }_{00}+{\gamma }_{01}{M}_j^{\left(2\right)}+u_{0j}$ ${\beta }_{1j}={\gamma }_{10}+{\gamma }_{11}{M}_j^{\left(2\right)}$ ${\beta }_{2j}={\gamma }_{20}$	$u_{0j}\sim N(0,{\tau }_{00}^2)$
MRT3-2R-1	L1: $Y_{\mathit{\text{ijk}}}={\pi }_{0\mathit{\text{jk}}}+{\pi }_{1\mathit{\text{jk}}}{M}_{\mathit{\text{ijk}}}^{(1)}+{\pi }_{2\mathit{\text{jk}}}{X}_{\mathit{\text{ijk}}}+e_{\mathit{\text{ijk}}}$	$e_{\mathit{\text{ijk}}}\sim N(0,{\sigma }_{1|M,X}^2)$
	L2: ${\pi }_{0\mathit{\text{jk}}}={\beta }_{00k}+{\beta }_{01k}{T}_{\mathit{\text{jk}}}+{\beta }_{02k}{W}_{\mathit{\text{jk}}}+r_{0\mathit{\text{jk}}}$ ${\pi }_{1\mathit{\text{jk}}}={\beta }_{10k}+{\beta }_{11k}{T}_{\mathit{\text{jk}}}+r_{1\mathit{\text{jk}}}$ ${\pi }_{2\mathit{\text{jk}}}={\beta }_{20k}$	$\left(\begin{array}{c}{r}_{0\mathit{\text{jk}}}\\ r_{1\mathit{\text{jk}}}\end{array}\right)\sim N\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\tau }_{00|T,W}^2& {\tau }_{01|T,W}\\ & {\tau }_{11|T}^2\end{array}\right)\right]$
	L3: ${\beta }_{00k}={\gamma }_{000}+u_{00k}$ ${\beta }_{01k}={\gamma }_{010}+u_{01k}$ ${\beta }_{02k}={\gamma }_{020}$ ${\beta }_{10k}={\gamma }_{100}+u_{10k}$ ${\beta }_{11k}={\gamma }_{110}+u_{11k}$ ${\beta }_{20k}={\gamma }_{200}$	$\left(\begin{array}{c}\begin{array}{c}{u}_{00k}\\ u_{01k}\\ u_{10k}\end{array}\\ u_{11k}\end{array}\right)\sim N\left[\left(\begin{array}{c}\begin{array}{c}0\\ 0\\ 0\end{array}\\ 0\end{array}\right),\left(\begin{array}{cccc}{\tau }_{0000}^2& {\tau }_{0001}& {\tau }_{0010}& {\tau }_{0011}\\ & {\tau }_{0101}^2& {\tau }_{0110}& {\tau }_{0111}\\ & & {\tau }_{1010}^2& {\tau }_{1011}\\ & & & {\tau }_{1111}^2\end{array}\right)\right]$
MRT3-2R-2	L1: $Y_{\mathit{\text{ijk}}}={\pi }_{0\mathit{\text{jk}}}+{\pi }_{1\mathit{\text{jk}}}{X}_{\mathit{\text{ijk}}}+e_{\mathit{\text{ijk}}},$	$e_{\mathit{\text{ijk}}}\sim N(0,{\sigma }_{1|X}^2)$
	L2: ${\pi }_{0\mathit{\text{jk}}}={\beta }_{00k}+{\beta }_{01k}{T}_{\mathit{\text{jk}}}+{\beta }_{02k}{T}_{\mathit{\text{jk}}}{M}_{\mathit{\text{jk}}}^{(2)}+{\beta }_{03k}{M}_{\mathit{\text{jk}}}^{(2)}+{\beta }_{04k}{W}_{\mathit{\text{jk}}}+r_{0\mathit{\text{jk}}}$ ${\pi }_{1\mathit{\text{jk}}}={\beta }_{10k}$	$r_{0\mathit{\text{jk}}}\sim N(0,{\tau }_{00|T,M,W}^2$)
	L3: ${\beta }_{00k}={\gamma }_{000}+u_{00k}$ ${\beta }_{01k}={\gamma }_{010}+u_{01k}$ ${\beta }_{02k}={\gamma }_{020}+u_{02k}$ ${\beta }_{03k}={\gamma }_{030}$ ${\beta }_{04k}={\gamma }_{040}$ ${\beta }_{10k}={\gamma }_{100}$	$\left(\begin{array}{c}{u}_{00k}\\ u_{01k}\\ u_{02k}\end{array}\right)\sim N\left[\left(\begin{array}{c}0\\ 0\\ 0\end{array}\right),\left(\begin{array}{ccc}{\tau }_{0000}^2& {\tau }_{0001}& {\tau }_{0002}\\ & {\tau }_{0101}^2& {\tau }_{0102}\\ & & {\tau }_{0202}^2\end{array}\right)\right]$
MRT3-2R-3	L1: $Y_{\mathit{\text{ijk}}}={\pi }_{0\mathit{\text{jk}}}+{\pi }_{1\mathit{\text{jk}}}{X}_{\mathit{\text{ijk}}}+e_{\mathit{\text{ijk}}}$	$e_{\mathit{\text{ijk}}}\sim N(0,{\sigma }_{1|X}^2)$
	L2: ${\pi }_{0\mathit{\text{jk}}}={\beta }_{00k}+{\beta }_{01k}{T}_{\mathit{\text{jk}}}+{\beta }_{02k}{W}_{\mathit{\text{jk}}}+r_{0\mathit{\text{jk}}}$ ${\pi }_{1\mathit{\text{jk}}}={\beta }_{10k}$	$r_{0\mathit{\text{jk}}}\sim N(0,{\tau }_{00|T,W}^2$)
	L3: ${\beta }_{00k}={\gamma }_{000}+{\gamma }_{001}{M}_k^{\left(3\right)}+u_{00k}$ ${\beta }_{01k}={\gamma }_{010}+{\gamma }_{011}{M}_k^{\left(3\right)}+u_{01k}$ ${\beta }_{02k}={\gamma }_{020}$ ${\beta }_{10k}={\gamma }_{100}$	$\left(\begin{array}{c}{u}_{00k}\\ u_{01k}\end{array}\right)\sim N\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\tau }_{0000|M}^2& {\tau }_{0001|M}\\ & {\tau }_{0101|M}^2\end{array}\right)\right]$
MRT3-2N-1	L1: $Y_{\mathit{\text{ijk}}}={\pi }_{0\mathit{\text{jk}}}+{\pi }_{1\mathit{\text{jk}}}{M}_{\mathit{\text{ijk}}}^{(1)}+{\pi }_{2\mathit{\text{jk}}}{X}_{\mathit{\text{ijk}}}+e_{\mathit{\text{ijk}}}$	$e_{\mathit{\text{ijk}}}\sim N(0,{\sigma }_{1|M,X}^2)$
	L2: ${\pi }_{0\mathit{\text{jk}}}={\beta }_{00k}+{\beta }_{01k}{T}_{\mathit{\text{jk}}}+{\beta }_{02k}{W}_{\mathit{\text{jk}}}+r_{0\mathit{\text{jk}}}$ ${\pi }_{1\mathit{\text{jk}}}={\beta }_{10k}+{\beta }_{11k}{T}_{\mathit{\text{jk}}}$ ${\pi }_{2\mathit{\text{jk}}}={\beta }_{20k}$	$r_{0\mathit{\text{jk}}}\sim N(0,{\tau }_{00|T,W}^2)$
	L3: ${\beta }_{00k}={\gamma }_{000}+u_{00k}$ ${\beta }_{01k}={\gamma }_{010}$ ${\beta }_{02k}={\gamma }_{020}$ ${\beta }_{10k}={\gamma }_{100}$ ${\beta }_{11k}={\gamma }_{110}$ ${\beta }_{20k}={\gamma }_{200}$	$u_{00k}\sim N(0,{\tau }_{0000}^2)$
MRT3-2N-2	L1: $Y_{\mathit{\text{ijk}}}={\pi }_{0\mathit{\text{jk}}}+{\pi }_{1\mathit{\text{jk}}}{X}_{\mathit{\text{ijk}}}+e_{\mathit{\text{ijk}}}$	$e_{\mathit{\text{ijk}}}\sim N(0,{\sigma }_{1|X}^2)$
	L2: ${\pi }_{0\mathit{\text{jk}}}={\beta }_{00k}+{\beta }_{01k}{T}_{\mathit{\text{jk}}}+{\beta }_{02k}{T}_{\mathit{\text{jk}}}{M}_{\mathit{\text{jk}}}^{(2)}+{\beta }_{03k}{M}_{\mathit{\text{jk}}}^{(2)}+{\beta }_{04k}{W}_{\mathit{\text{jk}}}+r_{0\mathit{\text{jk}}}$ ${\pi }_{1\mathit{\text{jk}}}={\beta }_{10k}$	$r_{0\mathit{\text{jk}}}\sim N(0,{\tau }_{00|T,M,W}^2$)
	L3: ${\beta }_{00k}={\gamma }_{000}+u_{00k}$ ${\beta }_{01k}={\gamma }_{010}$ ${\beta }_{02k}={\gamma }_{020}$ ${\beta }_{03k}={\gamma }_{030}$ ${\beta }_{04k}={\gamma }_{040}$ ${\beta }_{10k}={\gamma }_{100}$	$u_{00k}\sim N(0,{\tau }_{0000}^2)$
MRT3-2N-3	L1: $Y_{\mathit{\text{ijk}}}={\pi }_{0\mathit{\text{jk}}}+{\pi }_{1\mathit{\text{jk}}}{X}_{\mathit{\text{ijk}}}+e_{\mathit{\text{ijk}}}$	$e_{\mathit{\text{ijk}}}\sim N(0,{\sigma }_{1|X}^2)$
	L2: ${\pi }_{0\mathit{\text{jk}}}={\beta }_{00k}+{\beta }_{01k}{T}_{\mathit{\text{jk}}}+{\beta }_{02k}{W}_{\mathit{\text{jk}}}+r_{0\mathit{\text{jk}}}$ ${\pi }_{1\mathit{\text{jk}}}={\beta }_{10k}$	$r_{0\mathit{\text{jk}}}\sim N(0,{\tau }_{00|T,W}^2$)
	L3: ${\beta }_{00k}={\gamma }_{000}+{\gamma }_{001}{M}_k^{\left(3\right)}+u_{00k}$ ${\beta }_{01k}={\gamma }_{010}+{\gamma }_{011}{M}_k^{\left(3\right)}$ ${\beta }_{02k}={\gamma }_{020}$ ${\beta }_{10k}={\gamma }_{100}$	$u_{00k}\sim N(0,{\tau }_{0000|M}^2)$

Note. MRT2-1R-1 and MRT2-1R-2 stand for two-level MRTs with a level-1 and a level-2 moderator with random slopes, respectively. MRT2-1N-1 and MRT2-1N-2 stand for two-level MRTs with a level-1 and a level-2 moderator with nonrandomly varying slopes, respectively. MRT3-2R-1, MRT3-2R-2, and MRT3-2R-3 stand for three-level MRTs where treatment is at level 2 with a level-1, -2, -3 moderator with random slopes, respectively. MRT3-2N-1, MRT3-2N-2, and MRT3-2N-3 stand for three-level MCRTs where treatment is at level 2 with a level-1, -2, -3 moderator with nonrandomly varying slopes, respectively.

Table 2. List of design options and software modules.

1	2	3	4	5	6	7	8	9
Number of total levels of clustering	Model number	Level of treatment	Level of moderator	Slope of treatment or moderation	Binary moderator		Continuous moderator
					MDESD calculation	Power calculation	MDESD calculation	Power calculation
2	MRT2-1R-1	1	1	Random	MRT21R_MDESD	MRT21R_Power	MRT21Rc_MDESD	MRT21Rc_Power
	MRT2-1R-2	1	2	Random
	MRT2-1N-1	1	1	Nonrandomly Varying	MRT21N_MDESD	MRT21N_Power	MRT21Nc_MDESD	MRT21Nc_Power
	MRT2-1N-2	1	2	Nonrandomly Varying
3	MRT3-2R-1	2	1	Random	MRT32R_MDESD	MRT32R_Power	MRT32Rc_MDESD	MRT32Rc_Power
	MRT3-2R-2	2	2	Random
	MRT3-2R-3	2	3	Random
	MRT3-2N-1	2	1	Nonrandomly Varying	MRT32N_MDESD	MRT32N_Power	MRT32Nc_MDESD	MRT32Nc_Power
	MRT3-2N-2	2	2	Nonrandomly Varying
	MRT3-2N-3	2	3	Nonrandomly Varying

Figure 2. An example of MDESD calculation for binary moderators at level-1, -2, and -3 with random effects in three-level MCRT.

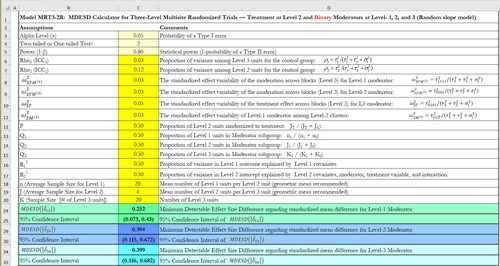
Figure 3. An example of power calculation for binary moderators at level-1, -2, and -3 with random effects in three-level MCRT.

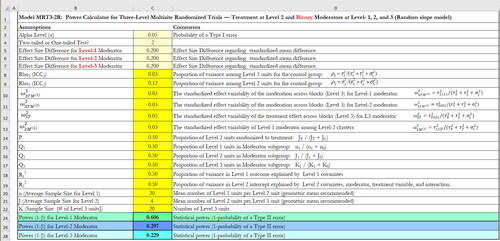
Table 3. MDESD and statistical power of three-level MCRTs.

Level of moderator	Slope of moderator effect	${\rho }_3$=0.03, ${\rho }_2$=0.12								${\rho }_3$=0.20, ${\rho }_2$=0.06
		MDESD				Power				MDESD				Power
		Binary moderator		Continuous moderator		Binary moderator		Continuous moderator		Binary moderator		Continuous moderator		Binary moderator		Continuous moderator
		K = 20	K = 40	K = 20	K = 40	K = 20	K = 40	K = 20	K = 40	K = 20	K = 40	K = 20	K = 40	K = 20	K = 40	K = 20	K = 40
1	Nonrandomly Varying	.183	.129	.091	.065	.866	.991	1.000	1.000	.171	.121	.085	.060	.908	.996	1.000	1.000
1	Random (${\omega }_{{3\mathit{\text{TM}}}^{(1)}}^2={\omega }_{{2M}^{(1)}}^2$ = 0.03)	.252	.173	.188	.130	.606	.900	.845	.991	.242	.166	.185	.127	.640	.921	.857	.993
1	Random (${\omega }_{{3\mathit{\text{TM}}}^{(1)}}^2={\omega }_{{2M}^{(1)}}^2$ = 0.05)	.284	.195	.230	.158	.506	.818	.683	.943	.276	.190	.227	.156	.530	.841	.693	.948
2	Nonrandomly Varying	.363	.255	.182	.127	.338	.595	.869	.993	.281	.197	.140	.098	.514	.813	.979	1.000
2	Random (${\omega }_{{3\mathit{\text{TM}}}^{(2)}}^2$ = 0.03)	.394	.271	.220	.152	.297	.544	.720	.959	.313	.215	.185	.127	.434	.741	.857	.993
2	Random (${\omega }_{{3\mathit{\text{TM}}}^{(2)}}^2$ = 0.05)	.404	.278	.239	.165	.284	.522	.649	.926	.326	.224	.207	.143	.405	.704	.771	.976
3	Nonrandomly Varying	.363	.255	.182	.127	.338	.595	.870	.993	.281	.197	.140	.098	.515	.813	.979	1.000
3	Random (${\omega }_{3T}^2$ = 0.05)	.399	.300	.199	.150	.229	.425	.800	.983	.346	.260	.173	.130	.296	.545	.938	.999
3	Random (${\omega }_{3T}^2$ = 0.10)	.469	.352	.234	.176	.176	.319	.615	.906	.424	.319	.212	.159	.207	.381	.729	.963

Note. Under the assumptions: n = 20, J = 4, p = 0.5, $R_1^2$ = $R_2^2$ = 0.5, $Q_1$ = $Q_2$ = $Q_3$ = 0.5 for binary moderators, power = 0.8 for the calculation of MDESD, and effect size difference = 0.2 for the calculation of power, a two-sided test with α = 0.05.

Figure 4. An example of power calculation for binary moderators at level-1 and -2 with random effects in two-level MIRTs.

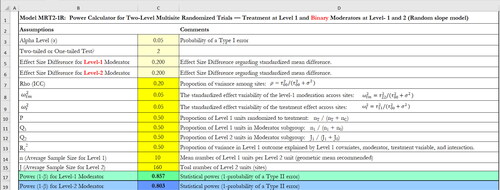
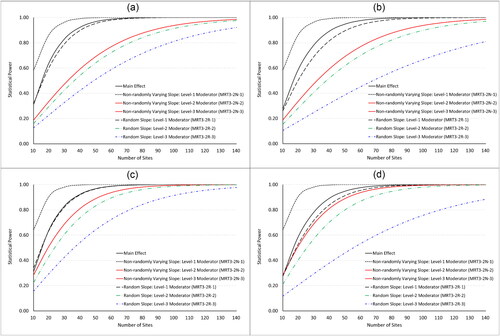
Figure 5. Power vs. site sample size for the analysis of main effects and binary moderator effects in three-level MCRTs.

Note. Under the assumptions: n = 20, J = 4, P = 0.5, $R_1^2$ = $R_2^2$ = 0.5, $Q_1$ = $Q_2$ = $Q_3$ = 0.5, effect size (standardized mean difference) for main effects = 0.2, effect size difference for binary moderator effects = 0.2, and a two-sided test with α = 0.05. ${\rho }_3$=0.03, ${\rho }_2$=0.12, ${\omega }_{{3\mathit{\text{TM}}}^{(1)}}^2={\omega }_{{2M}^{(1)}}^2$ = ${\omega }_{{3\mathit{\text{TM}}}^{(2)}}^2$ = 0.03, and ${\omega }_{3T}^2$ = 0.05 for random slope designs in Figure 5a. ${\rho }_3$=0.03, ${\rho }_2$=0.12, ${\omega }_{{3\mathit{\text{TM}}}^{(1)}}^2={\omega }_{{2M}^{(1)}}^2$ = ${\omega }_{{3\mathit{\text{TM}}}^{(2)}}^2$ = 0.05, and ${\omega }_{3T}^2$ = 0.10 for random slope designs in Figure 5b. ${\rho }_3$=0.20, ${\rho }_2$=0.06, ${\omega }_{{3\mathit{\text{TM}}}^{(1)}}^2={\omega }_{{2M}^{(1)}}^2$ = ${\omega }_{{3\mathit{\text{TM}}}^{(2)}}^2$ = 0.03, and ${\omega }_{3T}^2$ = 0.05 for random slope designs in Figure 5c. ${\rho }_3$=0.20, ${\rho }_2$=0.06, ${\omega }_{{3\mathit{\text{TM}}}^{(1)}}^2={\omega }_{{2M}^{(1)}}^2$ = ${\omega }_{{3\mathit{\text{TM}}}^{(2)}}^2$ = 0.05, and ${\omega }_{3T}^2$ = 0.10 for random slope designs in Figure 5d.

Table

Parameter	Comments	Resources
${\rho }_3$	Intraclass correlation coefficient at level 3: Proportion of variance among Level 3 units: ${\rho }_3={\tau }_3^2/({\tau }_3^2+{\tau }_2^2+{\sigma }_1^2).$	Social & Behavior: Dong et al. (2016); Jacob et al. (2010) Math: Wijekumar et al. (2009); Westine et al. (2013); McCoach et al. (2014); Shen et al. (2023); Zhu et al. (2012); Hedges and Hedberg (2013) Reading: Drummond et al. (2011); Wijekumar et al. (2014); Westine et al. (2013); Shen et al. (2023); Zhu et al. (2012) Science: Westine et al. (2013); Spybrook et al. (2016); Zhu et al. (2012)
${\rho }_2$	Intraclass correlation coefficient at level 2: Proportion of variance among Level 2 units: ${\rho }_2={\tau }_2^2/({\tau }_3^2+{\tau }_2^2+{\sigma }_1^2).$	Social & Behavior: Dong et al. (2016); Jacob et al. (2010) Math: Wijekumar et al. (2009); Westine et al. (2013); McCoach et al. (2014); Shen et al. (2023); Zhu et al. (2012); Hedges and Hedberg (2013) Reading: Drummond et al. (2011); Wijekumar et al. (2014); Westine et al. (2013); Shen et al. (2023); Zhu et al. (2012) Science: Westine et al. (2013); Spybrook et al. (2016); Zhu et al. (2012)
$R_2^2$	Proportion of variance in Level 2 intercept explained by Level 2 covariates	Social & Behavior: Dong et al. (2016); Jacob et al. (2010) Math: Wijekumar et al. (2009); Westine et al. (2013); McCoach et al. (2014); Shen et al. (2023); Zhu et al. (2012); Hedges and Hedberg (2013) Reading: Drummond et al. (2011); Wijekumar et al. (2014); Westine et al. (2013); Shen et al. (2023); Zhu et al. (2012) Science: Westine et al. (2013); Spybrook et al. (2016); Zhu et al. (2012)
$R_1^2$	Proportion of variance in Level 1 outcome explained by Level 1 covariates	Social & Behavior: Dong et al. (2016); Jacob et al. (2010) Math: Wijekumar et al. (2009); Westine et al. (2013); McCoach et al. (2014); Shen et al. (2023); Zhu et al. (2012); Hedges and Hedberg (2013) Reading: Drummond et al. (2011); Wijekumar et al. (2014); Westine et al. (2013); Shen et al. (2023); Zhu et al. (2012) Science: Westine et al. (2013); Spybrook et al. (2016); Zhu et al. (2012)
${\omega }_{3T}^2$	The standardized effect variability of the treatment effect across blocks (Level 3) for L3 moderator:${\omega }_{3T}^2={\tau }_{0101}^2/({\tau }_3^2+{\tau }_2^2+{\sigma }_1^2).$	Math: Wijekumar et al. (2009) Reading: Drummond et al. (2011); Wijekumar et al. (2014)

Table

Parameter	Comments	Resources
${\rho }_{}$	Intraclass correlation coefficient: Proportion of variance among Level 2 units: ${\rho }_{}={\tau }_{00}^2/({\tau }_{00}^2+{\sigma }_{}^2).$	Social & Behavior: Dong et al. (2016) Math: Westine et al. (2013); Hedges and Hedberg (2007); Bloom et al. (2007); Zhu et al. (2012) Reading: Drummond et al. (2011); Westine et al. (2013); Hedges and Hedberg (2007); Bloom et al. (2007); Zhu et al. (2012) Science: Spybrook et al. (2016); Zhu et al. (2012) Teacher outcomes: Kelcey and Phelps (2013a); Kelcey and Phelps (2013b)
$R_1^2$	Proportion of variance in Level 1 outcome explained by Level 1 covariates	Social & Behavior: Dong et al. (2016) Math: Westine et al. (2013); Hedges and Hedberg (2007); Bloom et al. (2007); Zhu et al. (2012) Reading: Drummond et al. (2011); Westine et al. (2013); Hedges and Hedberg (2007); Bloom et al. (2007); Zhu et al. (2012) Science: Spybrook et al. (2016); Zhu et al. (2012) Teacher outcomes: Kelcey and Phelps (2013a); Kelcey and Phelps (2013b)

Dong, N., Kelcey, B., & Spybrook, J. (2023a). Experimental design and power for moderation in multisite cluster randomized trials. The Journal of Experimental Education, 1–17. https://doi.org/10.1080/00220973.2023.2226934

 Web of Science ®Google Scholar

Dong, N., Reinke, W. M., Herman, K. C., Bradshaw, C. P., & Murray, D. W. (2016). Meaningful effect sizes, intraclass correlations, and proportions of variance explained by covariates for panning two- and three-level cluster randomized trials of social and behavioral outcomes. Evaluation Review, 40(4), 334–377. https://doi.org/10.1177/0193841X16671283

 PubMed Web of Science ®Google Scholar

Jacob, R., Zhu, P., & Bloom, H. (2010). New empirical evidence for the design of group randomized trials in education. Journal of Research on Educational Effectiveness, 3(2), 157–198. https://doi.org/10.1080/19345741003592428

 Google Scholar

Wijekumar, K., Hitchcock, J., Turner, H., Lei, P., & Peck, K. (2009). A multisite cluster randomized trial of the effects of compass learning Odyssey [R] math on the math achievement of selected grade 4 students in the Mid-Atlantic Region. Final Report. NCEE 2009-4068. National Center for Education Evaluation and Regional Assistance.

 Google Scholar

Westine, C. D., Spybrook, J., & Taylor, J. A. (2013). An empirical investigation of variance design parameters for planning cluster-randomized trials of science achievement. Evaluation Review, 37(6), 490–519. https://doi.org/10.1177/0193841X14531584

 PubMed Web of Science ®Google Scholar

McCoach, D. B., Gubbins, E. J., Foreman, J., Rubenstein, L. D., & Rambo-Hernandez, K. E. (2014). Evaluating the efficacy of using predifferentiated and enriched mathematics curricula for grade 3 students: A multisite cluster-randomized trial. Gifted Child Quarterly, 58(4), 272–286. https://doi.org/10.1177/0016986214547631

 Web of Science ®Google Scholar

Shen, Z., Curran, F. C., You, Y., Splett, J. W., & Zhang, H. (2023). Intraclass correlations for evaluating the effects of teacher empowerment programs on student educational outcomes. Educational Evaluation and Policy Analysis, 45(1), 134–156. https://doi.org/10.3102/01623737221111400

 Web of Science ®Google Scholar

Zhu, P., Jacob, R., Bloom, H., & Xu, Z. (2012). Designing and analyzing studies that randomize schools to estimate intervention effects on student academic outcomes without classroom-level information. Educational Evaluation and Policy Analysis, 34(1), 45–68. https://doi.org/10.3102/0162373711423786

 Web of Science ®Google Scholar

Hedges, L. V., & Hedberg, E. (2013). Intraclass correlations and covariate outcome correlations for planning two- and three-level cluster-randomized experiments in education. Evaluation Review, 37(6), 445–489. https://doi.org/10.1177/0193841X14529126

 PubMed Web of Science ®Google Scholar

Drummond, K., Chinen, M., Duncan, T. G., Miller, H., Fryer, L., Zmach, C., & Culp, K. (2011). Impact of the thinking reader [r] software program on grade 6 reading vocabulary, comprehension, strategies, and motivation: Final report. NCEE 2010-4035. National Center for Education Evaluation and Regional Assistance.

 Google Scholar

Wijekumar, K., Meyer, B. J., Lei, P. W., Lin, Y. C., Johnson, L. A., Spielvogel, J. A., Shurmatz, K. M., Ray, M., & Cook, M. (2014). Multisite randomized controlled trial examining intelligent tutoring of structure strategy for fifth-grade readers. Journal of Research on Educational Effectiveness, 7(4), 331–357. https://doi.org/10.1080/19345747.2013.853333

 Web of Science ®Google Scholar

Spybrook, J., Shi, R., & Kelcey, B. (2016). Progress in the past decade: An examination of the precision of cluster randomized trials funded by the U.S. institute of education sciences. International Journal of Research & Method in Education, 39(3), 255–267. https://doi.org/10.1080/1743727X.2016.1150454

 Web of Science ®Google Scholar

Hedges, L. V., & Hedberg, E. (2007). Intraclass correlation values for planning group randomized trials in education. Educational Evaluation and Policy Analysis, 29(1), 60–87. https://doi.org/10.3102/0162373707299706

 Web of Science ®Google Scholar

Bloom, H. S., Richburg-Hayes, L., & Black, A. R. (2007). Using covariates to improve precision for studies that randomize schools to evaluate educational interventions. Educational Evaluation and Policy Analysis, 29(1), 30–59. https://doi.org/10.3102/0162373707299550

 Web of Science ®Google Scholar

Kelcey, B., & Phelps, G. (2013a). Considerations for designing group randomized trials of professional development with teacher knowledge outcomes. Educational Evaluation and Policy Analysis, 35(3), 370–390. https://doi.org/10.3102/0162373713482766

 Web of Science ®Google Scholar

Kelcey, B., & Phelps, G. (2013b). Strategies for improving power in school-randomized studies of professional development. Evaluation Review, 37(6), 520–554. https://doi.org/10.1177/0193841X14528906

 PubMed Web of Science ®Google Scholar