Figures & data
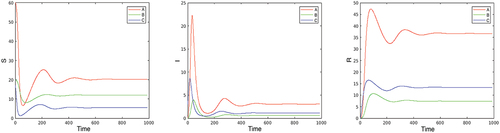
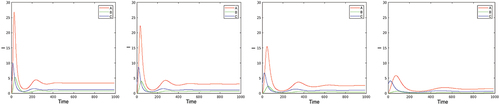
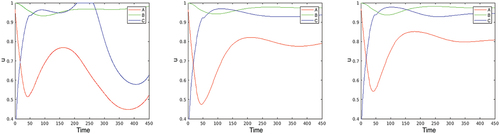
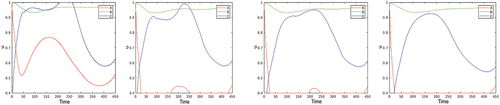
Figure 3. Optimization with respect to both and
in the benchmark case. The first two plots present the optimal controls
and
, the second three plots give the corresponding
,
, and
.
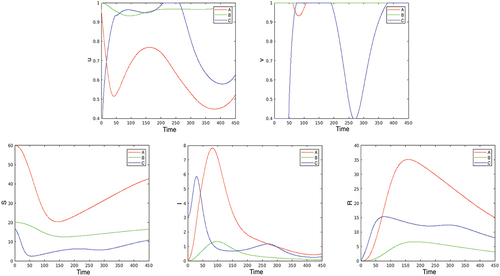
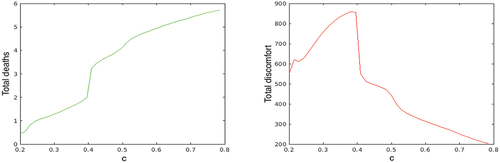
Figure 5. Infected population in the optimal solution for values of (first line), total number of deaths (second line left), and total “control energy”
(second line right)—called “discomfort” on the plot—on
as functions of
.
![Figure 5. Infected population in the optimal solution for values of α=0.2,0.3,0.4,0.5 (first line), total number of deaths (second line left), and total “control energy” E (second line right)—called “discomfort” on the plot—on [0,T] as functions of α.](/cms/asset/8b8220f4-212e-45e7-88c5-b95b4268962b/nmcm_a_2341693_f0005_oc.jpg)
Data availability statement
All data supporting the findings of this study are available within the paper.