On tracking varying bounds when forecasting bounded time series

Abstract

We consider a new framework where a continuous, though bounded, random variable has unobserved bounds that vary over time. In the context of univariate time series, we look at the bounds as parameters of the distribution of the bounded random variable. We introduce an extended log-likelihood estimation and design algorithms to track the bound through online maximum likelihood estimation. Since the resulting optimization problem is not convex, we make use of recent theoretical results on stochastic quasiconvex optimization, to eventually derive an Online Normalized Gradient Descent algorithm. We illustrate and discuss the workings of our approach based on both simulation studies and a real-world wind power forecasting problem.

Keywords:

• Generalized logit-normal distribution
• Normalized Gradient Descent
• Online quasiconvex optimization
• Inventory problem
• Wind power probabilistic forecasting

Disclaimer

As a service to authors and researchers we are providing this version of an accepted manuscript (AM). Copyediting, typesetting, and review of the resulting proofs will be undertaken on this manuscript before final publication of the Version of Record (VoR). During production and pre-press, errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal relate to these versions also.

1 Introduction

Many statistical applications involve response variables that are both continuous and bounded. This is especially the case when one has to deal with rates, percentages or proportions, for example when interested in the spread of an epidemic (Guolo and Varin, 2014), the unemployment rates in a given country (Wallis, 1987) or the proportion of time spent by animals in a certain activity (Cotgreave and Clayton, 1994). Indeed, proportional data are widely encountered within ecology-related statistical problems, see Warton and Hui (2011) among others. Similarly, when forecasting wind power generation, the response variable is also such a continuous bounded variable. Wind power generation is a stochastic process with continuous state space that is bounded from below by zero when there is no wind, and from above by the nominal capacity of the turbine (or wind farm) for high-enough wind speeds. More generally, renewable energy generation from both wind and solar energy are bounded stochastic processes, with the same lower bound (i.e., zero energy production) and different characteristics of their upper bound (since solar energy generation has a time-varying maximum depending on the time of day and time of year), see for example Pinson (2012) and Bacher et al. (2009).

These continuous bounded random variables call for probability distributions with a bounded support such as the beta distribution, truncated distributions or distributions of transformed normal variables as discussed by Johnson (1949). Often, the response variable is first assumed to lie in the unit interval $(0,1)$ and is then rescaled to any interval $(a,b)$. For applications involving such response variables, these bounds $(a,b)$ are always fixed to the same values over the sample. While this assumption makes sense in some cases, we argue it can be misleading and negatively impacts inference when the bounds $(a,b)$ actually vary over time or depending on exogenous variables whilst not being observed. In particular, it is highly relevant for energy applications, such as wind power forecasting, as the upper bound b may change over time, while being unknown, e.g., wind curtailment actions were taken and not (reliably) recorded. Another application is the inventory problem of the retailer (Laderman and Littauer, 1953). Let $X_t$ be the demand for a certain item at time t: $X_t$ is double-bounded, from below by zero and from above by the stock available at time t, i.e., by a time-varying upper bound $b_t$. To prepare for demand $X_{t+1}$, the retailer needs to find the quantity they should order in light of the knowledge they have of the past stocks and demands. Similar to the problem of forecasting wind power generation, the inventory problem involves a double-bounded random variable, the demand for a certain item, which can be regarded as a continuous variable at large quantities, with an upper bound that may vary over time whilst not being observed, e.g., in case of supply chain issues, information mismanagement or very large retailers that could not track the evolution of the stocks for each item, or would rather benefit from an automatic data-driven tracking.

In both those applications, if the random variable happens to get very close to the upper bound, it might be the case that a higher upper bound would have resulted in a higher wind power generation or item demand than the one that was observed. Therefore, we do not observe the true response. In that sense one could arguably think of it as being related to censoring and truncation. However, while truncation assumes the value of the response variable to be never seen (or recorded) if above the upper bound, and censoring assumes one does not know the exact value but does know it lies above the upper bound, we assume here that an upper bound lower than the true response results in squeezing the observed value of the variable, and thus in reshaping the probability distribution of the variable.

There are at least two ways of looking at varying bounds that cannot be observed. They can be introduced in the model as latent random variables A and B. Hence, the distribution of the response variable is conditional given A and B. The main advantage of this approach is its generality and flexibility, with A and B being distributed according to a well-specified probability distribution, which might depend on exogenous variables. Suppose we assume a parametric model for both the bounds and the response variable. Since we do not have access to the realizations of the bounds, the maximization of the likelihood might involve complicated high-dimensional integration, possibly computationally infeasible, and would therefore call for algorithms of the Expectation-Maximization kind (Dempster et al., 1977). Moreover, for forecasting applications, one needs to first compute (good enough) forecasts of the bounds in order to be able to forecast the response variable.

In the context of stochastic processes, varying bounds that cannot be observed can alternatively be considered as scaling parameters a and b of the parametric distribution of the bounded variable. Hence, a non-stationary framework is to be used for these additional parameters to be able to evolve over time. We will focus in this paper on discrete-time stochastic processes with a varying upper bound. Among the class of distributions with a bounded support, we choose the generalized logit-normal (GLN) distribution introduced by Mead (1965). The practical use of any family of distributions depends on the possible variation in its shape, and on the ease with which the distribution can be fitted. The GLN distribution is very flexible, and because the transformed variable is normally distributed, the probability density function (pdf) of the bounded variable $X_t$ can be expressed as a function of the standard normal density.

We aim to estimate the parameter vector $\theta$ of the pdf of $X_t$ that includes a bound parameter b through Maximum Likelihood Estimation (MLE). The first challenge we need to tackle when dealing with the bound as a parameter in a non-stationary setup is how to handle past observations that are out of the support $(0,b)$ of the bounded distribution of $X_t$ and make the log-likelihood infinite. We introduce a new term that relies on the sigmoid function to take into account those observations in a soft, finite way. Another challenge is that when considering the bound as a parameter, we cannot assume convexity anymore as the negative log-likelihood appears not to be convex with respect to (w.r.t.) the new bound parameter. Instead, we propose to assume quasiconvexity and use recent results from Hazan et al. (2015) about local quasiconvexity and Stochastic Normalized Gradient Descent (SNGD) to design an online algorithm. We present the statistical parametric model with a varying upper bound in Section 2 and the corresponding MLE in Section 3. In Section 4, we perform simulations of synthetic data to run the algorithm we proposed in Section 3. First we look at the performance when tracking the parameter vector $\theta$ over time, then when forecasting the probability distribution of the bounded variable. In Section 5, we provide 10-min-ahead probabilistic forecasts of the wind power generation at Anholt offshore wind farm (Denmark) using this new framework. Finally, we discuss the results, the limitations and some prospects of the methodology in Section 6.

2 Statistical model

2.1 Parametric distribution including the new parameter b

Let ${\tilde{X}}_t$ be a continuous bounded random variable, ${\tilde{X}}_t\in (0,1)$, and $X_t$ be the corresponding variable rescaled to $(0,b)$ by applying the transformation $X_t=b{\tilde{X}}_t$. The generalized logit transform $Y_t\in ℝ$ of $X_t\in (0,b)$ is given by$$Y_t=\gamma (X_t/b;\nu )=\hspace{0.17em}\log \hspace{0.17em}\frac{{(X_t/b)}^{\nu }}{1-{(X_t/b)}^{\nu }},\hspace{1em}\nu >0,$$

where $\nu$ is the shape parameter. When $Y_t$ is distributed according to a Gaussian distribution $\mathcal{N}(\mu ,{\sigma }^2)$, the original variable $X_t/b$ is then distributed according to a GLN distribution $L_{\nu }(\mu ,{\sigma }^2)$, see Frederic and Lad (2008) and Pinson (2012). To handle dependent observations, we assume the expectation of $Y_t$ to be an auto-regressive (AR) process of order p, ${\mu }_t={\sum }_{k=1}^p{\lambda }_k\gamma (x_{t-k}/b;\nu )$. Note that successive time points t are assumed to be spaced at uniform intervals. The pdf of $X_t$ conditional on the previous information set ${\mathcal{F}}_{t-1}$ (the $\sigma$-algebra generated by $X_1,\dots ,X_{t-1}$), with parameter vector $\theta =({\lambda }_1,\dots ,{\lambda }_p,{\sigma }^2,\nu ,b)$, is then(1) $$\begin{array}{c}{p}_{\theta }(x_t|{\mathcal{F}}_{t-1})=\{\begin{array}{cc}\frac{1}{\sqrt{2\pi {\sigma }^2}}\frac{\nu }{x_t\left(1-{(x_t/b)}^{\nu }\right)}\exp \hspace{0.17em}\left[-\frac{1}{2}{\left(\frac{\gamma (x_t/b;\nu )-{\mu }_t}{\sigma }\right)}^2\right]\hfill & \text{if}\mathrm{ }0<x_{t-k}<b,\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}\hfill \end{array}$$(1)

where $k=0,\dots ,p$.

2.2 Extended time-dependent log-likelihood function

We wish to estimate the parameter vector $\theta$ of the pdf $p_{\theta }(x_t|{\mathcal{F}}_{t-1})$ in (1) through MLE. In the case of a stationary time series and constant parameter $\theta$, this is equivalent to minimizing the negative log-likelihood objective function(2) $$-l(\theta )=-\sum _{t=p+1}^T\hspace{0.17em}\log \hspace{0.17em}{p}_{\theta }(x_t|{\mathcal{F}}_{t-1})$$(2)

w.r.t. $\theta$, the data sample $x_1,\dots ,x_T$ being fixed, assuming the random variables $X_t$ are independent and identically distributed (i.i.d.) conditional on ${\mathcal{F}}_{t-1}$. Note that we do not take into account the distribution of the first p observed values $(x_1,\dots ,x_p)$ and consider instead the likelihood conditional on them. For ease of notation and because the negative log-likelihood is to be minimized w.r.t. $\theta$, let $p_{\theta }(x_j|{\mathcal{F}}_{j-1})=p_j(\theta )$. In a non-stationary framework, an estimate of $\theta$ at time t can be retrieved by minimizing a time-dependent negative log-likelihood, such as(3) $$-l_t(\theta )=-\frac{1}{n_{\alpha }}\sum _{j=p+1}^t{\alpha }^{t-j}\hspace{0.17em}\log \hspace{0.17em}{p}_j(\theta ),$$(3)

where $\alpha \in (0,1]$, is an exponential forgetting factor and $n_{\alpha }=\frac{1}{1-\alpha }$ if $\alpha <1$, $n_{\alpha }=t-p$ if $\alpha =1$, is used to normalize the weighted negative log-likelihood. From (1) we can see that the negative log-likelihood in (2) we wish to minimize takes the value $+\infty$ as soon as an observation $x_t$ is greater or equal to b. This is an implicit constraint on b when estimating $\widehat{\theta }$. However, in a non-stationary framework we do not want b to be greater than all the observations $x_t$ as b should be able to vary over time. Let $U_t=\{p+1,,\dots ,t\}$, $C_t(\theta )=\{j\in U_t|x_{j-k}<b,k=0,\dots ,p\}$ and $\overline{C_t}(\theta )=\{j\in U_t|j\notin C_t(\theta )\}$, the complement of $C_t(\theta )$ in $U_t$. The log-likelihood takes finite values only for observations $x_j$ such that $j\in C_t(\theta )$. Therefore we can informally rewrite ${\sum }_{j=p+1}^t{\alpha }^{t-j}\hspace{0.17em}\log \hspace{0.17em}{p}_j(\theta )$ as $\sum _{j\in C_t(\theta )}{\alpha }^{t-j}\hspace{0.17em}\log \hspace{0.17em}{p}_j{|}_b(\theta )+\sum _{j\in \overline{C_t}(\theta )}{\alpha }^{t-j}\hspace{0.17em}\log \hspace{0.17em}0$, where $p_j{|}_b(\theta )$ is the pdf $p_j(\theta )$ restricted to its support $(0,b)$. When estimating the parameter vector at time t, we need to take into account all past observations, including the observations for which the log-likelihood does not take a finite value, i.e., including observations $x_j$ such that j does not belong to $C_t(\theta )$. Therefore, we propose to replace the value 0 in $\hspace{0.17em}\log \hspace{0.17em}0$, which originally corresponds to the value of the pdf $p_j(\theta )$ outside of its support, with a sigmoid function of $b-x_j$,(4) $$s_j(b)=\frac{1}{1+\hspace{0.17em}\exp \hspace{0.17em}(-b+x_j)}.$$(4)

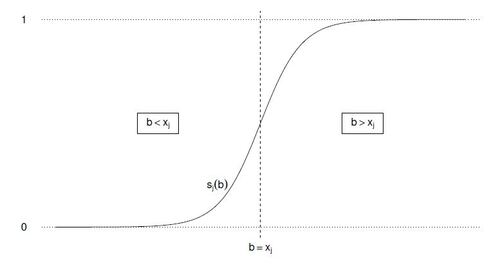
The function $s_j$ is illustrated in Figure 1. It can be seen as the probability of $x_j$ to be lower or equal than b: we have $s_j(b)\to 0^{+}$ when $b\ll x_j$ and $s_j(b)\to 1^{-}$ when $b\gg x_j$. Moreover, $-\hspace{0.17em}\log \hspace{0.17em}{s}_j(b)$ is convex and differentiable in b. Hence, we propose to use(5) $$-l_t^{\infty }(\theta )=-\frac{1}{n_{\alpha }}\left[\sum _{j\in C_t(\theta )}{\alpha }^{t-j}\hspace{0.17em}\log \hspace{0.17em}{p}_j(\theta )+\sum _{j\in \overline{C_t}(\theta )}{\alpha }^{t-j}\hspace{0.17em}\log \hspace{0.17em}{s}_j(b)\right],$$(5)

which we refer to as the extended time-dependent negative log-likelihood. One can note that $j\in \overline{C_t}(\theta )$ does not necessarily mean $x_j\ge b$ as it can happen because a lagged observation $x_{j-k}$ is such that $x_{j-k}\ge b$. In such a case, that is $j\in \overline{C_t}(\theta )$ and $x_j<b$, the observation $x_j$ will still increase the value of the total log-likelihood compared to the event $\{x_j\ge b\}$, which is also a nice feature of using $s_j$.

2.3 (Local-)Quasiconvexity

While convexity, or pseudoconvexity, have proved to be suitable assumptions for estimating the parameter vector of a GLN distribution (Pierrot and Pinson, 2021), this is not the case anymore when introducing the bound parameter b. Various simulations of $-l_t^{\infty }$ in (5) show the function not to be convex nor pseudoconvex in b, with plateau areas away from the optimal value $b^{*}$ and steep concave cliffs in the neighborhood of $b^{*}$. However, the same simulations also suggest that the function may still have a global minimum. There is a broader class of functions that include convex functions as a subclass and are still unimodal functions: quasiconvex functions. For simplicity, let us assume functions are differentiable. We use $\mathrm{\Vert }.\mathrm{\Vert }$ to denote the Euclidean norm. From Boyd and Vandenberghe (2010), a definition of quasiconvexity is

Definition 2.1 (Quasiconvexity)

A function $f:{ℝ}^d\to ℝ$ is called quasiconvex (or unimodal) if its domain and all its sublevel sets $$S_{\alpha }=\{\mathbf{x}\in \mathbf{dom}f|f(\mathbf{x})\le \alpha \},$$

for $\alpha \in ℝ$, are convex.

As an illustrative example, Figure 2 shows the negative pdf of a normal variable that is a quasiconvex function but not a convex function. While quasiconvexity is a considerable generalization of convexity, many of the properties of convex functions hold or have analogs for quasiconvex functions. However, quasiconvexity broadens but does not fully capture the notion of unimodality in several dimensions. This is the argument of Hazan et al. (2015) that introduced local-quasiconvexity, a property that extends quasiconvexity and captures unimodal functions that are not quasiconvex. Let ${\mathbb{B}}_d(\mathbf{x},r)$ denote the d dimensional Euclidean ball of radius r centered around $\mathbf{x}$, and ${\mathbb{B}}_d:={\mathbb{B}}_d(0,1)$. The definition of local-quasiconvexity as introduced by Hazan et al. (2015) is the following:

Definition 2.2 (Local-quasiconvexity)

Let $\mathbf{x},\mathbf{z}\in {ℝ}^d$, $\kappa ,\mathrm{ϵ}>0$.

We say that $f:{ℝ}^d\mapsto ℝ$ is $(\mathrm{ϵ},\kappa ,\mathbf{z})$-Strictly-Locally-QuasiConvex (SLQC) in $\mathbf{x}$, if at least one of the following applies:

1. $f(\mathbf{x})-f(\mathbf{z})\le \mathrm{ϵ}$ .

2. $\mathrm{\Vert }\nabla f(\mathbf{x})\mathrm{\Vert }>0$, and for every $\mathbf{y}\in {\mathbb{B}}_d(\mathbf{z},\mathrm{ϵ}/\kappa )$ it holds that $\nabla f{(\mathbf{x})}^{\mathrm{\top }}(\mathbf{y}-\mathbf{x})\le 0$ .

Hence, we propose to relax the convexity (or pseudoconvexity) assumption and instead rely on local-quasiconvexity when minimizing $-l_t^{\infty }$.

3 Online maximum likelihood estimation

3.1 Quasiconvex optimization

Let f be the quasiconvex objective function we wish to minimize w.r.t parameter $\mathbf{x}\in {ℝ}^d$. It is well known that quasiconvex problems can be solved through a series of convex feasibility problems (Boyd and Vandenberghe, 2010). However, solving such feasibility problems can be very costly and involves finding a family of convex functions ${\varphi }_t:{ℝ}^d\to ℝ$, $t\in ℝ$, which satisfy$$f(\mathbf{x})\le t\iff {\varphi }_t(\mathbf{x})\le 0,$$

and ${\varphi }_s(\mathbf{x})\le {\varphi }_t(\mathbf{x})$ whenever $s\ge t$. In the batch setup, a pioneering paper by Nesterov (1984) was the first to propose an efficient algorithm, Normalized Gradient Descent (NGD), and to prove that this algorithm converges to an $\mathrm{ϵ}$-optimal solution within $O(1/{\mathrm{ϵ}}^2)$ iterations given a differentiable quasiconvex objective function. Gradient Descent (GD) with fixed step sizes is known to perform poorly when the gradients are too small in a plateau area of the function or explode in cliff areas. Among the deep learning community, there have been several attempts to tackle plateaus and cliffs. However, those works do not provide a theoretical analysis showing better convergence guarantees than NGD. Having introduced SLQC functions, Hazan et al. (2015) prove that NGD also finds an $\mathrm{ϵ}$-optimal minimum for such functions within $O(1/{\mathrm{ϵ}}^2)$ iterations.

3.2 Online Normalized Gradient Descent

NGD can be used to minimize $-l_t^{\infty }$ w.r.t $\theta$. However, this implies to run NGD every time we want to update the parameter vector $\theta$. Taking advantage of the SLQC assumption, Hazan et al. (2015) presented SNGD, which is similar to Stochastic Gradient Descent (SGD) except they normalize the gradients, and prove the convergence of SNGD within $O(1/{\mathrm{ϵ}}^2)$ iterations to an $\mathrm{ϵ}$-optimal minimum. From the observation that online learning and stochastic optimization are closely related and interchangeable (see, e.g., Cesa-Bianchi et al. (2004) and Duchi et al. (2011)), we use the Stochastic Normalized Gradient Descent (SNGD) introduced by Hazan et al. (2015) and derive the corresponding Online Normalized Gradient Descent (ONGD) for online learning. ONGD is presented in Algorithm 1. To the best of our knowledge, this is the first time SNGD is used in an online learning fashion for Online Quasiconvex Optimization.

Algorithm 1 Online Normalized Gradient Descent (ONGD)

Input: convex set $\mathcal{K},T,{\theta }_m\in \mathcal{K}$, step size $\eta$, minibatch size mfor $t=m,\dots ,T$ do

Play ${\theta }_t$ and observe cost $f_t({\theta }_t)=\frac{1}{m}{\sum }_{j=t-m+1}^t{f}_j({\theta }_t)$.

Update and project:$$\begin{array}{cc}{\tilde{\theta }}_{t+1}\hfill & ={\theta }_t-\eta {\widehat{g}}_t\text{where}{g}_t=\nabla f_t({\theta }_t),{\widehat{g}}_t=\frac{g_t}{\mathrm{\Vert }{g}_t\mathrm{\Vert }}\hfill \\ {\theta }_{t+1}\hfill & ={\Pi }_{\mathcal{K}}({\tilde{\theta }}_{t+1})\hfill \end{array}$$

end for

Following the framework introduced by Cesa-Bianchi and Lugosi (2006), we define ONGD in terms of a repeated game played between the online players and the environment generating the outcome sequence. At each time t, we play a parameter vector ${\mathbf{x}}_t$. After we have committed to this choice, a cost function $f_t$ is revealed and the cost we incur is $f_t({\mathbf{x}}_t)$, the value of the cost function for the choice ${\mathbf{x}}_t$. Similar to Online Gradient Descent (OGD), which is based on standard gradient descent from offline optimization and was introduced in its online form by Zinkevich (2003), we have included in ONGD a projection step ${\Pi }_{\mathcal{K}}(.)$. Indeed, in each iteration, the algorithm takes a step from the previous point in the direction of the normalized gradient of the previous cost. This step may result in a point outside of the underlying convex set $\mathcal{K}$. In such cases the algorithm projects the point back to the convex set $\mathcal{K}$, i.e. finds its closest point in $\mathcal{K}$. SNGD requires the gradient to be estimated using a minibatch of minimal size m. Indeed, Hazan et al. (2015) provide a negative result showing that if the minibatch size is too small then the algorithm might diverge. This is where SNGD differs from SGD as in the latter and for the case of convex functions even a minibatch of size 1 is enough to ensure convergence.

GD methods update the current value of a parameter $\theta$ by taking a step in a descent direction, according to the gradient of the cost function f over a complete set of observations:(6) $${\widehat{\theta }}_{i+1}={\widehat{\theta }}_i-{\eta }_i\frac{1}{T}\sum _{j=1}^T{\nabla }_{\theta }f(x_j|{\widehat{\theta }}_i),$$(6)

where i is the current iteration and ${\eta }_i$ the step size at iteration i. Online/stochastic GD is obtained by dropping the averaging operation in (6) and updating the parameter $\theta$ according to(7) $${\widehat{\theta }}_{i+1}={\widehat{\theta }}_i-{\eta }_i{\nabla }_{\theta }f(x_i|{\widehat{\theta }}_i),$$(7)

where $x_i$ has been chosen randomly for SGD and $x_i$ are successive observations for OGD. The simplification relies on the hope that the random noise introduced by this procedure will not compromise the average behavior of the algorithm. Let $\alpha =1$ and $-l_t^{\infty }(\theta )=-\frac{1}{t-p}\left[\sum _{j\in C_t(\theta )}\hspace{0.17em}\log \hspace{0.17em}{p}_j(\theta )+\sum _{j\in \overline{C_t}(\theta )}\hspace{0.17em}\log \hspace{0.17em}{s}_j(b)\right]$. Hence, ONGD can be applied to our framework by taking$$\begin{array}{c}{f}_j({\theta }_t):=\{\begin{array}{cc}-\hspace{0.17em}\log \hspace{0.17em}{p}_j({\widehat{\theta }}_t)\hfill & \text{if}\mathrm{ }j\in C_t({\widehat{\theta }}_t),\hfill \\ -\hspace{0.17em}\log \hspace{0.17em}{s}_j({\widehat{b}}_t)\hfill & \text{if}\mathrm{ }j\in \overline{C_t}({\widehat{\theta }}_t).\hfill \end{array}\hfill \end{array}$$

When minimizing w.r.t $\theta =(\Lambda ,{\sigma }^2,\nu ,b)$, we shall recover positive estimates of the scale parameter ${\sigma }^2$ and the shape parameter $\nu$. This is constrained optimization that can be easily overcome by replacing ${\sigma }^2$ with $\omega =\hspace{0.17em}\log \hspace{0.17em}{\sigma }^2$ and $\nu$ with $\tau =\hspace{0.17em}\log \hspace{0.17em}\nu$. Such a change of variable allows us to avoid the projection step in Algorithm 1.

3.3 Recursive maximum likelihood estimation

A straightforward competitor to ONGD is a (classic) recursive MLE procedure. While suboptimal for non convex problems, such a recursive procedure is a quasi-Newton approach that approximates the Hessian with a positive definite matrix thanks to first-order information. Hence, the algorithm is ensured to run although its performance depends on how close the approximated Hessian is to the true Hessian. Recall that $n_{\alpha }=\frac{1}{1-\alpha }$. We can rewrite (5) as(8) $$\begin{array}{c}-l_t^{\infty }(\theta )=\{\begin{array}{cc}-\alpha l_{t-1}^{\infty }(\theta )-(1-\alpha )\hspace{0.17em}\log \hspace{0.17em}{p}_t(\theta )\hfill & \text{if}\mathrm{ }t\in C_t(\theta ),\hfill \\ -\alpha l_{t-1}^{\infty }(\theta )-(1-\alpha )\hspace{0.17em}\log \hspace{0.17em}{s}_t(b)\hfill & \text{if}\mathrm{ }t\in \overline{C_t}(\theta ).\hfill \end{array}\hfill \end{array}$$(8)

Let ${\widehat{\theta }}_t$ be the estimate of the parameter vector at time t. The recursive MLE procedure relies on a Newton step for obtaining ${\widehat{\theta }}_t$ as a function of ${\widehat{\theta }}_{t-1}$, see, e.g., Madsen (2007) and Pinson and Madsen (2012). Let ${\mathbf{h}}_t={\nabla }_{\theta }\hspace{0.17em}\log \hspace{0.17em}{p}_t({\widehat{\theta }}_{t-1})$ if $t\in C_t({\widehat{\theta }}_{t-1})$, ${\mathbf{h}}_t={\nabla }_{\theta }\hspace{0.17em}\log \hspace{0.17em}{s}_t({\widehat{b}}_{t-1})$ if $t\in \overline{C_t}({\widehat{\theta }}_{t-1})$ and ${\widehat{\mathbf{R}}}_t=-{\nabla }_{\theta }^2{l}_t^{\infty }({\widehat{\theta }}_t)$. Our two-step recursive scheme at time t is$$\begin{array}{cc}{\widehat{\mathbf{R}}}_t\hfill & =\alpha {\widehat{\mathbf{R}}}_{t-1}+(1-\alpha ){\mathbf{h}}_t{\mathbf{h}}_t^{\mathrm{\top }},\hfill \\ {\widehat{\theta }}_t\hfill & ={\widehat{\theta }}_{t-1}+(1-\alpha ){\widehat{\mathbf{R}}}_t^{-1}{\mathbf{h}}_t.\hfill \end{array}$$

An algorithm based upon such a scheme might face computational issues as it requires inverting the information matrix ${\widehat{\mathbf{R}}}_t$, at each iteration. This can be prevented by directly working with the matrix inverse, the covariance matrix ${\widehat{\mathbf{P}}}_t$. The resulting algorithm (rMLE.b) is described in Algorithm 2.

Algorithm 2 Recursive Maximum Likelihood Estimation (rMLE.b)

Input: $T,{\theta }_p\in {ℝ}^{p+3}$, forgetting factor $\alpha \in (0,1)$, ${\widehat{\mathbf{P}}}_p={10}^6{\mathbf{I}}_{p+3}$for $t=p+1,\dots ,T$ do

Set ${\mathbf{h}}_t={\nabla }_{\theta }\hspace{0.17em}\log \hspace{0.17em}{p}_t({\widehat{\theta }}_{t-1})$ if $t\in C_t({\widehat{\theta }}_{t-1})$ or set ${\mathbf{h}}_t={\nabla }_{\theta }\hspace{0.17em}\log \hspace{0.17em}{s}_t({\widehat{\theta }}_{t-1})$ if $t\in \overline{C_t}({\widehat{\theta }}_{t-1})$.

Update:$$\begin{array}{cc}{\widehat{\mathbf{P}}}_t\hfill & =\frac{1}{\alpha }\left[{\mathbf{I}}_{p+3}-\frac{{\widehat{\mathbf{P}}}_{t-1}{\mathbf{h}}_t{\mathbf{h}}_t^{\mathrm{\top }}}{\frac{\alpha }{1-\alpha }+{\mathbf{h}}_t^{\mathrm{\top }}{\widehat{\mathbf{P}}}_{t-1}{\mathbf{h}}_t}\right]{\widehat{\mathbf{P}}}_{t-1}\hfill \\ {\widehat{\theta }}_t\hfill & ={\widehat{\theta }}_{t-1}+(1-\alpha ){\widehat{\mathbf{P}}}_t{\mathbf{h}}_t\text{if}\hspace{0.17em}t>T_0+p\hfill \end{array}$$end for

The technical derivations and detailed computations required for Algorithms 1 and 2 are available in the supplementary material.

4 Simulation study

We perform an empirical study on synthetic data to check on the behaviour of ONGD, in particular in comparison with a classic recursive MLE procedure, i.e., rMLE.b. We run 100 Monte Carlo (MC) simulations with $T=12000$, $\lambda =0.9$, ${\sigma }^2=1$, $\nu =1.5$. Only the bound parameter b is simulated so that it varies over time. Hence, in Section 4.1, while we test the tracking ability of our algorithms regarding b, we also control their ability to retrieve constant parameters, i.e., $\lambda$, ${\sigma }^2$ and $\nu$. Then, in Section 4.2, we introduce the task of issuing predictive distributions using the tracked parameters and evaluate the algorithms depending on the sharpness and calibration of these forecasts.

4.1 Tracking the parameter vector

The lag $p=1$ of the AR process is assumed to be known and the initial values of the parameter vector $\theta =(\lambda ,{\sigma }^2,\nu ,b)$ are set to $(0,1,1,1)$. From a theoretical point of view, these initial values only need to be feasible, i.e., ${\sigma }_0^2>0$, ${\nu }_0>0$ and $b_0=1$. We (a priori) choose ${\sigma }_0^2=1$ and ${\nu }_0=1$ because they are standard values. The values of the hyperparameters m and $\eta$ for ONGD, $\alpha$ for rMLE.b, are empirically selected. We test a grid of values for each hyperparameter and select the values that achieve the best tracking/accuracy trade-off on the first MC simulation. The same values are then used on the 99 remaining MC simulations. These values are listed in Table 1. ONGD runs as soon as m observations are available, while rMLE.b runs from p observations on but needs a warm-up period $T_0=200$ to update the covariance matrix ${\widehat{\mathbf{P}}}_t$ before starting updating the parameters. Note that the computational complexity is $\mathcal{O}(\mathit{Tmp})$ for ONGD and $\mathcal{O}(T{p}^2)$ for rMLE.b. Running Algorithms 1 and 2 to track the parameter vector over the 100 synthetic time series of our simulation study took about 10 seconds and 4 seconds, respectively. We used a 12-core CPU MacBook M3 Pro Chip with 18GB unified memory and parallel computation over 5 cores.

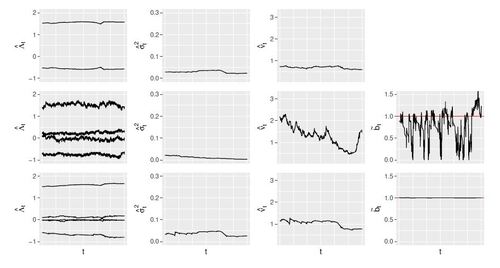
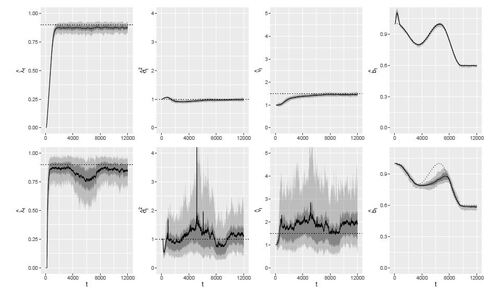
We provide in Figure 3 the plots of $-l_t^{\infty }$ for the first MC simulation, $t=3000$ and $\alpha =0.975$ w.r.t. each parameter, the other parameters being fixed to their true values. From the function being not convex in b, it is clear that the optimization problem cannot be assumed to be convex when introducing an upper bound parameter b. The tracked parameters averaged over the simulations are presented in Figure 4 along with corresponding MC intervals. ONGD manages to accurately estimate both time-varying and constant parameters while rMLE.b performs well in tracking a decreasing b, but fails to properly track an increasing b. Moreover, this comes with a cost in accuracy that is very high for constant parameters. The estimation of ${\sigma }^2$ and $\nu$ is also rather unstable. Note that ${\sigma }^2$ is already at its true value when the algorithms get started and allows us to control that there is no divergence from the optimal value. As a matter of fact and as stated by Hazan et al. (2015), for ONGD we have observed the divergence of ${\sigma }^2$ when the minibatch size m was too small, i.e., for $m<10$.

4.2 Forecasting the distribution

As many applications that might benefit from this framework involve forecasting, we are now interested in the performance of the algorithms when forecasting at time t the distribution of the bounded variable $X_{t+1}$. To be able to track the bound parameter b over time, we have introduced in Section 2 the extended time-dependent negative log-likelihood $-l_t^{\infty }$, which makes sense from an inference point of view. As we are working with series of dependent observations, when moving to forecasting the distribution of $X_{t+1}$, we need the current value $b_t$ of b to be greater than all the p former observed values of $X_t,\dots ,X_{t-p+1}$ for the expected value of $X_{t+1}$ to exist. Therefore, we introduce a projection step as described in Section 1 for ONGD: we project ${\widehat{\theta }}_t$ on the convex set $\mathcal{K}={\mathrm{R}}^{p+2}\times (\max (x_t,\dots ,x_{t-p+1}),+\infty )$ and we get the projected parameter ${\tilde{\theta }}_t={\Pi }_{\mathcal{K}}({\widehat{\theta }}_t)=({\widehat{\Lambda }}_t,{\widehat{\omega }}_t,{\widehat{\tau }}_t,{\tilde{b}}_t)$ where ${\tilde{b}}_t=\max (x_t,\dots ,x_{t-p+1})+\delta$ if $\max (x_t,\dots ,x_{t-p+1})>{\widehat{b}}_t$, ${\tilde{b}}_t={\widehat{b}}_t$ if $\max (x_t,\dots ,x_{t-p+1})<{\widehat{b}}_t$. Note that we need to introduce a small $\delta >0$ as we project ${\widehat{b}}_t$ on an open convex set. When looking at the observation $x_t$ as a coarsened version of $X_t$, $\delta$ can be seen as a coarsening parameter. This coarsened data framework has been formalized by Heitjan and Rubin (1991) and Heitjan (1993). We use $\delta =0.001$.

We evaluate the predictive distributions through proper scoring rules. Scoring rules are attractive measures of predictive performance as they evaluate calibration and sharpness simultaneously. The paradigm of maximizing the sharpness subject to calibration was proposed in Gneiting et al. (2007) under the conjecture that ideal forecasts and the maximization of sharpness subject to calibration are equivalent. Not only are scoring rules measures of both calibration and sharpness, they also incentivize truthful calibrated and informative forecasts when they are proper for the class of predictive distributions at hand (Holzmann and Eulert, 2014). We use the Continuous Ranked Probability Score (CRPS) that is a proper scoring rule relative to the class $\mathcal{P}$ of the Borel probability measures on $\mathrm{R}$ (Gneiting and Raftery, 2007). Proper scoring rules are often used in negative orientation, e.g., the lower the better. As we work with predictive densities, one could think of using the logarithmic score, which is strictly proper relative to all measures that are absolutely continuous. However, in our framework it can always happen that $x_{t+1}$ falls outside the support of the predictive density ${\widehat{p}}_{t+1}$ we have issued at time t, when the current estimate ${\widehat{b}}_t$ of the upper bound is too low. In such a case, the logarithmic score is equal to $-\hspace{0.17em}\log \hspace{0.17em}{\widehat{p}}_{t+1}(x_{t+1})=-\hspace{0.17em}\log \hspace{0.17em}0=+\infty$, which is not suitable. In contrast, let us identify a probabilistic forecast with its cumulative distribution function (cdf) F. For continuous variables, the CRPS is defined on $\mathrm{R}$ as(9) $$\text{CRPS}(F,x)={\int }_{-\infty }^{\infty }{\left(F(y)-{\mathrm{1}}_{y\ge x}\right)}^2\mathrm{d}y,$$(9)

where x is the evaluation point. Let $F:={\widehat{F}}_{t+1}$ and $x:=x_{t+1}$. When $x_{t+1}<{\widehat{b}}_t$, i.e., the observation $x_{t+1}$ is inside the support of the predictive distribution ${\widehat{F}}_{t+1}$, we have(10) $$\text{CRPS}({\widehat{F}}_{t+1},x_{t+1})={\int }_{-\infty }^{{\widehat{b}}_t}{\left({\widehat{F}}_{t+1}(y)-{\mathrm{1}}_{y\ge x_{t+1}}\right)}^2\mathrm{d}y.$$(10)

Now when $x_{t+1}\ge {\widehat{b}}_t$, i.e., the observation $x_{t+1}$ is outside the support of the predictive distribution ${\widehat{F}}_{t+1}$, we have(11) $$\text{CRPS}({\widehat{F}}_{t+1},x_{t+1})={\int }_{-\infty }^{{\widehat{b}}_t}{\left({\widehat{F}}_{t+1}(y)-{\mathrm{1}}_{y\ge x_{t+1}}\right)}^2\mathrm{d}y+x_{t+1}-{\widehat{b}}_t.$$(11)

Note that ${\widehat{F}}_{t+1}$ and ${\widehat{b}}_t$ are fixed to the same values in (10) and (11) while only $x_{t+1}$ varies. It is straightforward to see that for a same forecast ${\widehat{F}}_{t+1}$, the CRPS increases when $x_{t+1}$ is outside the support of the predictive distribution ${\widehat{F}}_{t+1}$, compared to $x_{t+1}$ being inside. However, contrary to the logarithmic score that becomes infinite, the CRPS is only increased to a higher finite value. Lastly, the CRPS allows us to compare discrete and continuous distributions, that is to compare our density-based algorithms to usual benchmarks such as climatology and probabilistic persistence. Indeed, if the predictive distribution takes the form of a sample of size N, then the right side of (9) can be evaluated in $\mathcal{O}(N\hspace{0.17em}\log \hspace{0.17em}N)$ operations (Hersbach, 2000). Climatology is based on all data available at the time of forecasting and probabilistic persistence is the last observed value, which we dress with the past persistence errors. We also evaluate the predictive distributions issued by rMLE.1, i.e., by the usual recursive MLE when the bound is assumed to be fixed and equal to 1 (Pierrot and Pinson, 2021).

We start computing predictive distributions after 2,000 observations. Recall that the hyperparameters were chosen in Section 4.1 upon looking at only the first MC simulation, but the whole simulated time series, i.e., the data we are now computing probabilistic forecasts for. This may be optimistic, even if we only looked at the data from the first MC simulation. In order for our algorithms to not be more optimistic than the benchmarks, we use the hyperparameters for probabilistic persistence and rMLE.1 that give the best CRPS on the first MC simulation. The CRPS are available in Table 2. The average CRPS obtained by the ideal forecaster, i.e., the GLN distribution with the true values $\lambda$, ${\sigma }^2$, $\nu$, $b_{t-p+1},\dots ,b_{t+1}$, is 5.782%. Probabilistic persistence performs very well on our synthetic dataset with a CRPS that is already much closer to the ideal forecaster’s than climatology’s. ONGD, which properly handles the varying upper bound, shows a CRPS that is very close to the ideal forecaster’s. Moving from rMLE.1 to ONGD provides a significant improvement, which is similar to moving from probabilistic persistence to rMLE.1. As for ONGD’s natural competitor rMLE.b, it does not manage to improve the results of rMLE.1 significantly.

To specifically check on probabilistic and marginal calibration, Probability Integral Transform (PIT) histograms and marginal calibration plots are available in the supplementary material.

5 Application to wind power forecasting

Accurately forecasting wind power generation is highly important for the integration of wind energy into power systems. We are interested in very short-term forecasting, that is in lead times of a few minutes, which is not only crucial for transmission system operators to keep the system in balance but also very difficult to improve the forecasts for, especially compared to the simple but very efficient persistence.

5.1 Data description

We have historical data from a large offshore wind farm, Anholt in Denmark, from July 1, 2013 to August 31, 2014. The active power is available for 110 wind turbines at a temporal resolution of every 10 minutes. We normalize each time series individually according to the nominal power of the wind turbine, and compute the average generation over the wind farm depending on the number of wind turbines that are available at each time t in order to handle missing values. The response random variable we wish to forecast at time t is $X_{t+1}\in (0,1)$, the average active power generated by the wind farm at time $t+1$. As stated in Section 4.2, we choose to look at the observation $x_t$ as a coarsened version of $X_t$ with $\delta =0.001$. Hence, an observation $x_t$ is set to $\delta$ if $x_t<\delta$ and to $1-\delta$ if $x_t>1-\delta$ and $x_t\in [\delta ,1-\delta ]$ whereas $X_t\in (0,1)$.

5.2 Validation setup

We split our dataset into two datasets that we keep separate: a training/cross-validation dataset from July 1, 2013 to March 31, 2014, resulting in 39,450 observations; a test dataset from April 1 to August 31, 2014, resulting in 22,029 observations. As in Section 4.2, we compare Algorithms 1 and 2 to climatology, probabilistic persistence and rMLE.1. For methods involving hyperparameters, namely probabilistic persistence, rMLE.1, ONGD and rMLE.b, we choose the hyperparameters upon CRPS-based cross-validation: we run each competing algorithm from the beginning of the training set, issue the corresponding probabilistic forecasts, and select the hyperparameters that give the lowest CRPS on the cross-validation dataset, i.e., data from November 1, 2013 to March 31, 2014. The subsequent hyperparameter values are available in Table 3.

Running Algorithms 1 and 2 to track the parameter vector over the entire dataset took 0.98 seconds and 0.60 seconds, respectively. We used a 12-core CPU MacBook M3 Pro Chip with 18GB unified memory.

5.3 Assessment of the probabilistic forecasts

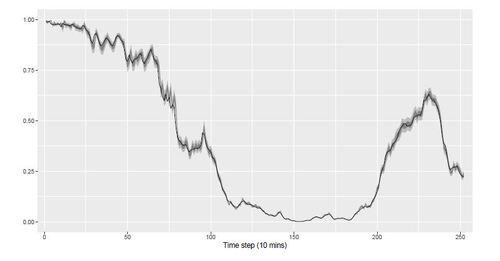
The probabilistic forecasts associated with each algorithm are assessed on the test set. The corresponding CRPS are presented in Table 4. Again, probabilistic persistence improves the CRPS of climatology by a large percentage already and both rMLE algorithms perform similarly. As for ONGD, the improvement over both persistence and rMLE.1 is very significant and much larger than the one observed during the simulation study. The parameters tracked by rMLE.1 and Algorithms 1and 2 are plotted for some sub-sample of the test set in Figure 5. We plot the projection ${\tilde{b}}_t$ of ${\widehat{b}}_t$, see Section 4.2, to display the upper bound that is actually used for prediction. The estimates of the parameter vector $\Lambda$ are consistent between ONGD and rMLE.b, while more noisy for ONGD. The parameter estimates from rMLE.1 and rMLE.b are in general very close to one another and show similar patterns. Indeed, rMLE.b does not manage to track a varying upper bound since the estimated ${\widehat{b}}_t$ does not vary significantly away from 1. Only ONGD captures variations of the bound parameter b below 1. When selecting the hyperparameters, we observed a significant improvement on the cross-validation set for a minibatch size $m=1$ only, the values tested for $m\in \{1,5,10,20,50,100,150\}$. By looking at the parameter estimates, we noticed that for $m=5$ the bound estimate was also varying away from 1, but more slowly and closer to 1. When looking at the power generation itself, the bound tracked by ONGD for $m=1$ does make sense. This result and the generalization performance of the model are confirmed on the test set, since the CRPS we get is very close to the one we got on the cross-validation set. Therefore, it seems that these data call for a very aggressive choice of m, so that the algorithm can track the bound. In return some noise is introduced into the other parameter estimates.

In Figure 6, we provide the probabilistic forecasts of ONGD over a 36-hour period of time on the test set. One can note that the prediction intervals are tight. When looking at probabilistic calibration, the PIT histogram shows a large number of very low and very high PIT values, which suggests that the predictive distributions issued by ONGD are underdispersed. However, when an observation falls outside of the prediction interval, it does not fall far away, which explains the very good CRPS achieved by ONGD overall. PIT histograms and marginal calibration plots for all algorithms are available in the supplementary material.

6 Discussion

We have introduced a framework, where we aim to track varying bounds for bounded time series as well as an extended time-dependent negative log-likelihood to deal with this new framework. As the objective functions at hand are not convex anymore, we have proposed to use the broader local-quasiconvexity assumption through an online algorithm. To compete with this quasiconvexity framework and online algorithm, we have also proposed a more usual recursive MLE procedure. We have run these algorithms on both a synthetic and a real dataset to track the parameters of a time series distribution over time, including the upper bound of the support of the distribution. Then, we have presented how to use such a new framework for forecasting.

The algorithm we propose in this new framework is an online algorithm that is directly derived from SNGD and, similarly to ordinary OGD, only relies on the negative log-likelihood we observe at time t for our current set of parameters. It no longer requires any kind of forgetting action and only asks for the usual step size when updating the parameter vector through the gradient at time t. A new hyperparameter that is related to a specificity of SNGD is the size m of the minibatch, since SNGD is not guaranteed to converge for $m=1$, unlike SGD. This algorithm performs very well on our simulated examples, with performances very close to the ideal forecaster. When applied to wind power forecasting, it improved the CRPS of probabilistic persistence by more than 30% on the test set. However, the predictive distributions do not achieve probabilistic calibration, as the prediction intervals appear to be too narrow in general. It is worth noting that ONGD required to set the minibatch size m to 1 on the wind power generation dataset in order to be able to track the upper bound. This is quite aggressive and suggests that this kind of data may call for methods that can handle big jumps in the bound values.

We challenged ONGD with two competitors, both of which relying on recursive MLE: rMLE.1 and rMLE.b. The former operates in the usual framework when the upper bound is assumed to be fixed to 1, while the latter is as straightforward adaptation of rMLE.1 in the context of a varying upper bound. These algorithms showed similar performances on both synthetic and real data, with rMLE.b failing to properly track a varying upper bound. Since this is, to the best of our knowledge, the first time such a framework with varying bounds has been studied, further research could explore different assumptions, e.g., on the stochastic process the distribution of the bounded variable, or a lower bound.

SUPPLEMENTARY MATERIAL

Calculation details:

Technical derivations and details that are required by the computations for Algorithms 1 and 2. (.pdf file)

Additional plots:

PIT histograms and marginal calibration plots for all competing algorithms in the simulation study and the application to wind power forecasting. (.pdf file)

R project:

R scripts for the simulation study in Section 4, along with the corresponding synthetic data. All outputs necessary for the study can be reproduced with the corresponding scripts and are also provided. The structure and content of the R project is described in a README file. (.zip file)

Table 1: Hyperparameter values for each algorithm: step size $\eta$ and minibatch size m (Algorithm 1) and forgetting factor $\alpha$ (Algorithm 2)

	$\eta$	m	$\alpha$
Algorithm 1: ONGD	0.001	100	–
Algorithm 2: rMLE.b	–	–	0.975

Table 2: 1-step-ahead CRPS and respective improvement over persistence and rMLE.1. The CRPS is averaged over the MC samples, and the standard deviation is also provided.

	mean (sd)	Imp./persist.	Imp./rMLE.1
ideal forecaster	5.782% (0.095)	–	–
climatology	15.258% (0.237)	–	–
probabilistic persistence	6.279% (0.097)	–	–
rMLE.1	6.042% (0.087)	3.78%	–
Algorithm 1: ONGD	5.807% (0.095)	7.52%	3.89%
Algorithm 2: rMLE.b	6.035% (0.110)	3.89%	0.11%

Table 3: Hyperparameter values for each algorithm: order p of the AR process, step size $\eta$, minibatch size m and forgetting factor $\alpha$.

	p	$\eta$	m	$\alpha$
Algorithm 1: ONGD	4	0.03	1	–
Algorithm 2: rMLE.b	5	–	–	0.9982

Table 4: 10-minute-ahead CRPS and respective improvements over probabilistic persistence and rMLE.1.

	CRPS	Imp./persist.	Imp./rMLE.1
climatology	22.033%	–	–
probabilistic persistence	1.350%	–	–
rMLE.1	1.082%	19.89%	–
Algorithm 1: ONGD	0.888%	34.22%	17.89%
Algorithm 2: rMLE.b	1.056%	21.83%	2.43%
*Best forecast bolded.

Figure 1: Sigmoid function $s_j(b)$ on the real line.

Figure 2: A quasiconvex differentiable function on $ℝ$, the negative density of a normal variable, with plateau areas when going away from the global minimum.

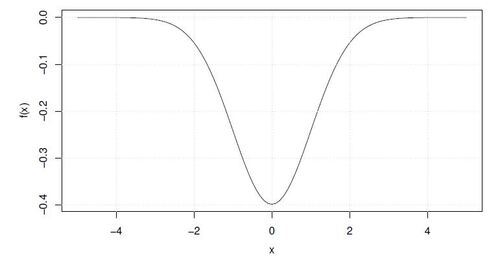
Figure 3: The extended time-dependent negative log-likelihood for the first MC simulation, $t=3000$, $\alpha =0.975$, w.r.t. $\lambda$ (top left), $\omega$ (top right), $\tau$ (bottom left) and b (bottom right). For each plot, the remaining parameters are set to their true values.

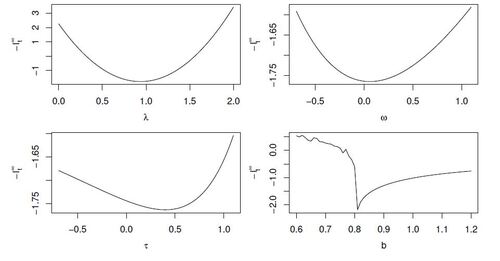
Figure 4: Confidence intervals of the tracked parameters for ONGD (top) and rMLE.b (bottom) with coverage probabilities 0.9 and 0.5, along with the average estimates (solid lines) and the true parameters (dotted lines).

Figure 5: Estimates ${\widehat{\Lambda }}_t$, ${\widehat{\sigma }}_t^2$, ${\widehat{\nu }}_t$ and projected estimate ${\tilde{b}}_t$ on a sub-sample of the test set for rMLE.1 (top), ONGD (center) and rMLE.b (bottom).

Figure 6: Probabilistic forecasts from ONGD, based on prediction intervals with nominal coverage rates of 95 and 75%, along with power measurements (solid black line).