Global stability analysis and modelling onchocerciasis transmission dynamics with control measures

ABSTRACT

Background: Onchocerciasis infection is one of the neglected tropical diseases targeted for eradication by 2030. The disease is usually transmitted to humans through the bites of black flies. These black flies mostly breed near well-oxygenated fast-running water bodies. The disease is common in mostly remote agricultural villages near rivers and streams.

Objective: In this study, a deterministic model describing the infection dynamics of human onchocerciasis disease with control measures is presented.

Methods: We derived the model’s reproductive number and used a stability theorem of a Metzler matrix to show that disease-free equilibrium is both locally and globally asymptotically stable whenever the reproductive number is less than one. Parameter contribution was conducted using sensitivity analysis. The model endemic equation is shown to be a cubic polynomial in the presence of infected immigrants and a quadratic form in their absence.

Results: When the inflow of infected immigrants is null, the model endemic equation may admit a unique equilibrium if the reproductive number is greater than one, or admits multiple endemic equilibria if the reproductive number is less than unity. We carried out a sensitivity analysis to identify the significant parameters that contribute to onchocerciasis spread.

Conclusion: Onchocerciasis disease can be eradicated if the importation of infected immigrants is properly monitored. The integration of the One Health concept in the public health system is key in tackling the emergence and spread of diseases.

KEYWORDS:

• Onchocerciasis
• bifurcation
• sensitivity analysis
• global stability
• basic reproductive number

Introduction

Onchocerciasis popularly called river blindness or Robles’ disease is among the 11 most important neglected tropical diseases targeted for eradication by 2030 [1]. This disease is transmitted to humans through the bites of black fly of the genus Simulium. The disease is common in Africa and this calls for urgent attention. Neglected tropical diseases need urgent attention in developing countries at large. The fight against these diseases in developing countries is paramount.

These black flies breed near well oxygenated fast-running water bodies [2]. The immature phases of the black fly (egg, larva and pupa) are aquatic. As a result, the disease is common in most remote agricultural villages near rivers and streams [3].

The people who are mostly at risk of black fly bites include farmers, tourists, missionaries/evangelists, peace keepers, field researchers and volunteers [4]. In West Africa, the fear of infection is one of the major causes of human migration from fertile river basins into the sub marginal lands, which results in over cultivation and low productivity [5].

Currently, about 218 million people globally is at risk of onchocerciasis transmissions. Over 99% of infected people dwell in Tropical Africa while the remaining live in Yemen and Latin America [6].

In 2017, it was estimated that 14.6 million of the people infected with onchocerca volvulus had developed various skin diseases and 1.15 million people had loss their vision according to a report by CDC-Onchocerciasis-Epidemiology and risk factors, 2019.

Figure 1 shows the Worldwide distribution of Onchocerca volvulus [6]. The disease is endemic in Western, Central and Eastern Africa. Northern and Southern Africa are free from the infection.

Figure 1. Human onchocerciasis reported cases in Ghana from 2008–2015.

The continued existence of black fly vectors, the co-endemicity of onchocerciasis with Loa-loa, the inflow of infected immigrants and the lack of proper knowledge about onchocerciasis disease constitute a major threat to the elimination efforts of this disease especially in Africa [2,7,8]. In Ghana, for example, onchocerciasis is found in isolated remote farming communities near rivers and streams. And this make the disease control very challenging.

Up to date, no vaccine nor medication for the prevention of onchocerciasis disease exist. Hence, mass drug administration with ivermectin has so far remained the only effective control strategy in the fight against this disease. However several studies have demonstrated that the complete elimination of the disease may not be feasible or may required a longer period of time especially in Africa with ivermectin drug alone [3,7]. Thus, alternative control measures including supplementary vector control strategies are recommended to accelerate the onchocerciasis elimination drive [2,7–9].

Hence, improving our comprehension of the dynamics of the disease transmission using mathematical modeling is necessary in order to design effective control techniques [10,11].

Mathematical models generally explain the dynamics of infections, the threshold value that determines the persistence or die out of the infection and the best control measures in combating diseases [12–16].

Several mathematical models have been used to evaluate intervention strategies concerning onchocerciasis disease [3,8,12,17,18]. Authors in [3] adopted the theory of optimal control and explored the effectiveness of controls such as personal protection, treatment with ivermectin and vector control used to combat onchocerciasis diseases. Their results indicated that vector control was the best among the controls considered. However, it was concluded that eliminating onchocerciasis from the population depends on ivermectin treatment as well as vector control. The work done in [4], an SIR model of river blindness disease with demography was formulated. The results suggested that the endemicity of onchocerciasis represent a major health risk to the communities in northern Nigeria. It was also observed that there is a decline in the susceptibility rate. And this was probably due to the intervention by health workers in terms of treatment and education. According to [19], combining ivermectin treatment with larviciding and trapping of black flies can significantly reduce onchocerciasis transmission rate. The analysis of a mathematical model for onchocerciasis presented in [20] revealed that combining ivermectin mass drug administration with educational campaigns, larviciding and trapping of black flies can significantly reduce the spread of onchocerciasis. These authors, however recommended that future onchocerciasis models should endeavor to explore the influence of infected immigrants on onchocerciasis transmission dynamics.

Following the recommendations in [20], we formulated and analyzed a simple model for the infection dynamics of onchocerciasis that takes into account educational campaigns, ivermectin treatment, black fly larvae control, black fly trapping and the inflow of infected immigrants.

Educational campaign is aimed at creating awareness about onchocerciasis and it’s main causes. Educate the public on preventive measures and the mode of treatment. Education can also help unveil the misconceptions and myths surrounding onchocerciasis. Larviciding is intended to control the black fly numbers in the community [20]. Trapping of black flies refers to the process of using all kind of traps and baits to collect and remove black flies in the communities [8].

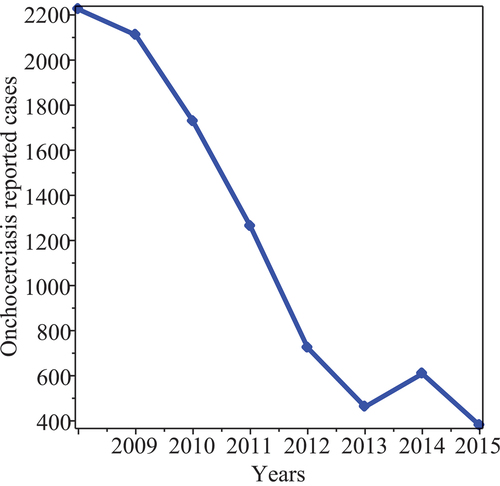
Table 1 and Figure 1 show reported cases of onchocerciasis between 2008–2015. There is a decline in the number of reported cases of the disease.

Table 1. Human onchocerciasis reported cases in Ghana from 2008 to 2015.

Year	Cases	Cummulative cases
2008	2225	2225
2009	2111	4336
2010	1728	6064
2011	1263	7327
2012	724	8051
2013	462	8513
2014	609	9122
2015	380	9502

Table 2 shows the number of reported cases of individuals treated for human onchocerciasis in Ghana from 2005–2019. This is evident that the disease needs urgent attention in Ghana.

Table 2. Reported number of individuals treated for human onchocerciasis in Ghana from 2005 to 2019.

Year	Individuals treated
2019	6526501
2018	6441223
2017	4403121
2016	4331666
2015	3416583
2014	3372058
2013	3372058
2012	3466716
2011	1776626
2010	1491516
2009	544959
2008	1784353
2007	No data
2006	1069137
2005	675066

Onchocerciasis model description and formulation

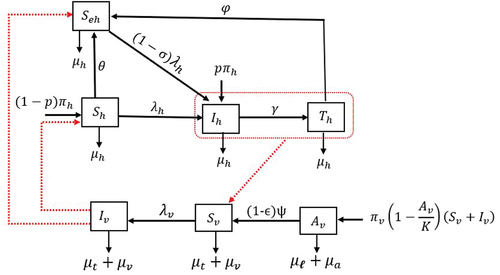
The model considered the interactions of human (host) and black fly (vector) populations. Humans (hosts) are classified into susceptible $(S_h)$, susceptible educated $(S_{\mathit{eh}})$, infected $(I_h)$ and treated $(T_h)$ subclasses. As a result, the total human population at any given time t is:

(1) $\left(N_h\left(\mathit{t}\right)=S_h\left(\mathit{t}\right)+S_{\mathit{eh}}\left(\mathit{t}\right)+I_h\left(\mathit{t}\right)+T_h\left(\mathit{t}\right)\right)$(1)

Following the model formulation in [21], the total host population is sustained at a constant rate ${\pi }_h$ that includes birth and immigration of which a small fraction p are infected immigrants. Thus, humans are recruited into the susceptible class at a rate $(1-\mathit{p}){\pi }_h$. Susceptible humans receive education on the disease through campaigns and move to susceptible educated class upon compliance at a rate $\mathit{\theta }$. Susceptible and susceptible educated humans become infected through contact with infected vectors at a rate ${\lambda }_h$ and $(1-\mathit{\sigma }){\lambda }_h$, respectively. Where $\mathit{\sigma }$ is the efficacy of educational campaign. Infected humans receive ivermectin drug through mass administration and progress to treated class at a rate $\mathit{\gamma }$. Treated humans become susceptible educated at a rate $\mathit{\phi }$ as the results of the sterilizing effect of ivermectin drug. A good number of studies have reported that humans receiving ivermectin treatment are still transmitting onchocerciasis [20,22,23]. Thus, in this model, $\mathit{r}\in [0,1)$ is a modification parameter used to account for the reduction in transmission of infections from treated hosts. ${\mu }_h$ is the human removal rate from each human compartment.

Also, the total black fly vector population is stratified into immature black fly and adults black fly sub-populations. The immature sub-population consists of the black fly eggs, larvae and pupae stages. These stages form the aquatic phase of the black fly.

For computational simplicity, all the aquatic stages are lumped into a single compartment denoted by $\left(A_v\right)$. The aquatic vector $\left(A_v\right)$ is generated by the eggs laid by the female adults’ black fly (susceptible and infected) at a rate $\left({\pi }_v\left(1-\frac{A_v}{\mathit{K}}\right)\left(S_v+I_v\right)\right)$.

The population of aquatic vector is bounded above by the carrying capacity $(\mathit{K})$ which depends on the breeding site, food, fresh air and well oxygenated water supply. Aquatic vector populations decline due to natural death at a rate of $\left({\mu }_a\right)$ and to larviciding at a rate of $\left({\mu }_{\mathrm{\ell }}\right)$. The surviving aquatic vectors mature into susceptible black flies at a rate $\left(1-\mathit{\epsilon }\right)\mathit{\psi }$, where $\mathit{\epsilon }$ is the efficacy of larviciding. The matured black fly sub-population is divided into susceptible $\left(S_v\right)$ and infected $\left(I_v\right)$ vectors. The susceptible black fly become infected during blood meal from infected or treated humans at a rate $\left({\lambda }_v\right)$. As the results of natural death and trapping at rates $\left({\mu }_v\right)$ and $\left({\mu }_t\right)$, respectively, the susceptible $\left(S_v\right)$ and infected $\left(I_v\right)$ black fly population decreases. Thus, at any time t, the total black fly population is:

(2) $\left(N_v\left(\mathit{t}\right)=A_v\left(\mathit{t}\right)+S_v\left(\mathit{t}\right)+I_v\left(\mathit{t}\right)\right)$(2)

The forces of infection for the human and black fly are, respectively, $\left({\lambda }_h=\frac{b{\beta }_h{I}_v}{N_h}\right)$ and $\left({\lambda }_v=\frac{b{\beta }_v(I_h+\mathit{r}{T}_h)}{N_h}\right)$. The transfer diagram in Figure 2 describes the transmission dynamics of human onchocerciasis. The state variables and our model parameters are presented in Tables 3 and 4, respectively.

Figure 2. Transfer diagram for the onchocerciasis transmission dynamics.

Table 3. Description of state variables of the model.

Variable	Description
$S_h$	Susceptible humans
$S_{\mathit{eh}}$	Susceptible educated humans
$I_h$	Infected humans
$T_h$	Treated humans
$A_v$	Immature black flies
$S_v$	Susceptible black flies
$I_v$	Infected black flies
$N_h$	Total human population
$N_v$	Total black fly population
${\lambda }_h$	Force of infection for the human population
${\lambda }_v$	Force of infection for the black fly (vector)

Table 4. Parameter description. susceptible human

Parameter	Description
${\pi }_h$	Human recruitment rate
${\mu }_h$	Natural death rate of human
${\beta }_h$	Prob. of transmission of infections from an infected human to a susceptible black fly
$\mathit{p}$	Proportion of infected immigrants
$\mathit{\theta }$	Educational campaign compliance rate
$\mathit{\sigma }$	Efficacy of educational campaign
$\mathit{\gamma }$	Progression rate of infected humans to treated humans
$\mathit{\phi }$	Progression rate from treated human to susceptible educated humans
$\mathit{r}$	Modification parameter accounting for the reduction of transmission of infections from a treated human to a susceptible black fly
${\pi }_v$	Black fly egg deposition rate
$\mathit{K}$	Carrying capacity of aquatic vector
$\mathit{b}$	Black fly biting rate
${\beta }_v$	Probability of transmission of infections from an infected black fly to a susceptible human
$\mathit{\psi }$	Maturity rate of immature black fly
$\mathit{\epsilon }$	Efficacy of larviciding
${\mu }_v$	Natural death rate of mature black fly
${\mu }_a$	Natural death rate of immature black fly
${\mu }_{\mathrm{\ell }}$	Death rate of immature black fly due to larviciding
${\mu }_t$	Death rate of mature black fly due to trapping

The model system of equations becomes:

(3) $\left\{\begin{array}{c}\frac{d{S}_h}{\mathit{dt}}=(1-\mathit{p}){\pi }_h-({\lambda }_h+q_1)S_h-\mathit{\theta }{S}_h\\ \frac{\mathit{d}{\mathit{S}}_{\mathit{eh}}}{\mathit{dt}}=\mathit{\theta }{S}_h+\mathit{\phi }{T}_h-(q_0{\lambda }_h+{\mu }_h)S_{\mathit{eh}}\\ \frac{d{I}_h}{\mathit{dt}}=\mathit{p}{\pi }_h+{\lambda }_h{S}_h+q_0{\lambda }_h{S}_{\mathit{eh}}-q_2{I}_h\\ \frac{d{T}_h}{\mathit{dt}}=\mathit{\gamma }{I}_h-q_3{T}_h\\ \frac{d{A}_v}{\mathit{dt}}={\pi }_v\left(1-\frac{A_v}{\mathit{K}}\right)\left(S_v+I_v\right)-[\left(1-\mathit{\epsilon }\right)\mathit{\psi }+u_1]A_v\\ \frac{d{S}_v}{\mathit{dt}}=\left(1-\mathit{\epsilon }\right)\mathit{\psi }{A}_v-({\lambda }_v+u_2)S_v\\ \frac{d{I}_v}{\mathit{dt}}={\lambda }_v{S}_v-u_2{I}_v\end{array}\right.$(3)

where,

$q_0=1-\mathit{\sigma },q_1=\mathit{\theta }+{\mu }_h,q_2=\mathit{\gamma }+{\mu }_h,q_3=\mathit{\phi }+{\mu }_h,u_1={\mu }_{\mathrm{\ell }}+{\mu }_a\mathit{and}{u}_2={\mu }_t+{\mu }_v$

Boundedness of solution

Theorem 1:

For non-negative initial values $S_h(0),S_{\mathit{eh}}(0),I_h(0),T_h(0),A_v(0),S_v(0)\mathrm{and}{I}_v(0)$ of system 3, the solutions $S_h(\mathit{t}),S_{\mathit{eh}}(\mathit{t}),I_h(\mathit{t}),T_h(\mathit{t}),A_v(\mathit{t}),S_v(\mathit{t})\mathrm{and}{I}_v(\mathit{t})$ are all non-negative and bounded $\mathrm{\forall }\mathrm{t}\ge 0.$

Proof: Consider the system of differential equation in 3

(4) $\begin{array}{rl}& \frac{d{S}_h}{\mathit{dt}}=(1-\mathit{p}){\pi }_h-({\lambda }_h+q_1)S_h\\ & \frac{d{S}_h}{\mathit{dt}}\ge -({\lambda }_h+q_1)S_h\\ & \frac{d{S}_h}{\mathit{dt}}\ge -({\lambda }_h+q_1)S_h\\ & \int \frac{d{S}_h}{S_h}\ge -\int ({\lambda }_h+q_1)\mathit{dt}\\ & S_h(\mathit{t})\ge S_h(0)e^{-(q_1\mathit{t}+{\int }_0^t{\lambda }_h(\mathit{\tau })\mathit{d\tau })}\ge 0\end{array}$(4)

Similarly, the following results can be obtained:

$\begin{array}{cc}{S}_{\mathit{eh}}(\mathit{t})& \ge S_{\mathit{eh}}(0)e^{-({\mu }_h\mathit{t}+q_0{\int }_0^t{\lambda }_h(\mathit{\tau })\mathit{d\tau })}\ge 0\\ I_h(\mathit{t})& \ge I_h(0)e^{-q_2\mathit{t}}\ge 0\\ T_h(\mathit{t})& \ge T_h(0)e^{-q_3\mathit{t}}\ge 0\\ A_v(\mathit{t})& \ge A_v(0)e^{-[(1-\epsilon )\psi +u_1]\mathit{t}}\ge 0\\ S_v(\mathit{t})& \ge S_v(0)e^{-(u_2\mathit{t}+{\int }_0^t{\lambda }_v(\mathit{\tau })\mathit{d\tau })}\ge 0\\ I_v(\mathit{t})& \ge I_v(0)e^{-u_2\mathit{t}}\ge 0\end{array}$

Therefore, for $\mathrm{\forall }$ t $\ge$ 0, the state variables of the model have non-negative solutions [24].

Invariant region

This section is dedicated to finding the region over which the solution set of our onchocerciasis model system of equations is well posed.

Theorem 2:

The feasible region in which the solution set of the model system of equations make biological sense is the set;

(5) $\mathit{\Omega }=\left\{\left({\Omega }_h,{\Omega }_v\right)\in {ℝ}_{+}^4\times {ℝ}_{+}^3\right\}$(5)

where

(6) ${\mathrm{\Omega }}_h=\left\{(S_h,S_{\mathit{eh}},I_h,T_h)\in R_{+}^4:S_h+S_{\mathit{eh}}+I_h+T_h\le \frac{{\pi }_h}{{\mu }_h}\right\}$(6)

and

(7) ${\Omega }_v=\left\{(A_v,S_v,I_v)\in {ℝ}_{+}^3:A_v\le \mathit{K},S_v+I_v\le \frac{(1-\mathit{\epsilon })\mathit{\psi K}}{u_2}\right\}$(7)

Proof: First, we determine the subset ${\mathrm{\Omega }}_h$.

The human (host) population $N_h$ at any given time t is:

(8) $N_h=S_h+S_{\mathit{eh}}+I_h+T_h$(8)

(9) $\frac{d{N}_h}{\mathit{dt}}=\frac{d{S}_h}{\mathit{dt}}+\frac{\mathit{d}{\mathit{S}}_{\mathit{eh}}}{\mathit{dt}}+\frac{d{I}_h}{\mathit{dt}}+\frac{d{T}_h}{\mathit{dt}}$(9)

(10) $\frac{d{N}_h}{\mathit{dt}}={\pi }_h-{\mu }_h{N}_h$(10)

Solving equation (10)(10) $\frac{d{N}_h}{\mathit{dt}}={\pi }_h-{\mu }_h{N}_h$(10) and taking the limit as $\mathit{t}\to +\mathrm{\infty }$ we obtain: $N_h\to \frac{{\pi }_h}{{\mu }_h}$

Consequently, the following result is obtained

(11) $0\le N_h\le \frac{{\pi }_h}{{\mu }_h}$(11)

Therefore;

(12) ${\Omega }_h=\left\{\left(S_h,S_{\mathit{eh}},I_h,T_h\right)\in {ℝ}_{+}^4:S_h+S_{\mathit{eh}}+I_h+T_h\le \frac{{\mathit{\pi }}_{\mathit{h}}}{{\mu }_h}\right\}$(12)

Secondly, the subset ${\mathrm{\Omega }}_v$ is determined. At any point in time, the blackfly (vector) population satisfies:

(13) $A_v\le \mathit{K},N_{\mathit{mv}}=S_v+I_v$(13)

(14) $\Rightarrow \frac{\mathit{d}{\mathit{N}}_{\mathit{mv}}}{\mathit{dt}}=\frac{d{S}_v}{\mathit{dt}}+\frac{d{I}_v}{\mathit{dt}}$(14)

$\begin{array}{rl}& \Rightarrow \frac{\mathit{d}{\mathit{N}}_{\mathit{mv}}}{\mathit{dt}}\le \left(1-\mathit{\epsilon }\right)\mathit{\psi K}-u_2{N}_{\mathit{mv}}\\ & \Rightarrow N_{\mathit{mv}}-\frac{(1-\mathit{\epsilon })\mathit{\psi K}}{u_2}\le \left(N_{\mathit{mv}}(0)-\frac{(1-\mathit{\epsilon })\mathit{\psi K}}{u_2}\right)e^{-u_2\mathit{t}}\\ & \Rightarrow N_{\mathit{mv}}\le \frac{(1-\mathit{\epsilon })\mathit{\psi K}}{u_2}\mathrm{as}\mathit{t}\to +\mathrm{\infty }.\end{array}$

(15) $\text{Therefore},{\Omega }_v=\left\{\left(A_v,S_v,I_v\right)\in {ℝ}_{+}^3:A_v\le \mathit{K},S_v+I_v\le \frac{(1-\mathit{\epsilon })\mathit{\psi K}}{u_2}\right\}$(15)

Thus, the feasible region for the solution set of the model system of equations is:

(16) $\mathit{\Omega }=\left\{\left({\Omega }_h,{\Omega }_v\right)\in {ℝ}_{+}^4\times {ℝ}_{+}^3\right\}$(16)

Onchocerciasis-free equilibrium

In computing the disease-free equilibria, we employ the theorem below.

Theorem 3: Let’s define

(17) $\mathcal{N}=\frac{{\pi }_v\left(1-\mathit{\epsilon }\right)\mathit{\psi }}{u_2\left[\left(1-\mathit{\epsilon }\right)\mathit{\psi }+u_1\right]}$(17)

as the black fly net reproduction or extinction number, then if:

1. $\mathcal{N}\le 1$, model 3 has a trivial disease-free equilibrium (TDFE) (black fly extinction equilibrium point) given by:

   (18) ${\xi }_0=\left(\frac{{\pi }_h}{q_1},\frac{\theta {\pi }_h}{q_1{\mu }_h},0,0,0,0,0\right)$(18)

2. $\mathcal{N}>1$ (black flies persist in the community), model (3) admits a realistic disease-free equilibrium (RDFE) given by:

   (19) ${\xi }_1=\left(\frac{{\pi }_h}{q_1},\frac{\theta {\pi }_h}{q_1{\mu }_h},0,0,\mathit{K}\left(1-\frac{1}{\mathcal{N}}\right),\frac{\mathit{K}\left(1-\mathit{\epsilon }\right)\psi }{u_2}\left(1-\frac{1}{\mathcal{N}}\right),0\right)$(19)

Proof:

Suppose, $\left(S_h^{\ast },S_{eh}^{\ast },I_h^{\ast },T_h^{\ast },A_v^{\ast },S_v^{\ast },I_v^{\ast }\right)$ is the disease-free equilibrium point. Setting the right-hand side of system 3 to zero with the condition that there are no infections at the disease-free equilibrium, that is, $I_h^{\ast }=T_h^{\ast }=I_v^{\ast }=\mathit{p}=0$, yields:

(20) $S_h^{\ast }=\frac{{\pi }_h}{q_1}$(20)

(21) $S_{eh}^{\ast }=\frac{\theta S_h^{\ast }}{{\mu }_h}=\frac{\theta {\pi }_h}{q_1{\mu }_h}$(21)

(22) $A_v^{\ast }=0\mathrm{or}\mathit{K}\left(1-\frac{1}{\mathcal{N}}\right)$(22)

(23) $S_v^{\ast }=0\mathrm{or}\frac{\mathit{K}\left(1-\mathit{\epsilon }\right)\psi \left(1-\frac{1}{\mathcal{N}}\right)}{u_2}$(23)

Hence, ${\xi }_0$ and ${\xi }_1$ are obtained, respectively, from $A_v^{\ast }=0$ and $A_v^{\ast }=\mathit{K}\left(1-\frac{1}{\mathcal{N}}\right)$. Clearly, the magnitude of $\mathcal{N}$ dictates the existence of the model disease-free equilibrium points.

$\mathcal{N}$ is a threshold quantity similar to the vector offspring number or net reproduction number used in [25–30]. In general, this can be interpreted as a measure of the average number of new adult female black flies produced by one reproductive black fly during its entire reproductive life. It is expressed as a product of the egg deposition rate ${\pi }_v$, the fraction of immature black fly that survive and develop into adult black fly $\frac{\left(1-\mathit{\epsilon }\right)\psi }{\left[\left(1-\mathit{\epsilon }\right)\psi +u_1\right]}$ (in the presence of larviciding and vector trapping) and the average life span of adult black fly $\frac{1}{u_2}$. Thus, if $\mathcal{N}>1$, the black fly population persist in the community, otherwise if $\mathcal{N}\le 1$, the black fly vector population becomes extinct and the Onchocerciasis transmission can be eliminated. It is worth noting that the trivial disease-free equilibrium (TDFE) corresponds to the absence of black fly vectors in the community. Hence, the TDFE is biologically less meaningful.

Onchocerciasis reproduction number

Expressing our model differential equations in the form $\frac{\mathit{dX}}{\mathit{dt}}=(\mathit{F}-\mathit{V})X^T$ where $X^T$ denotes the transpose of $\mathit{X}=(I_h,T_h,I_v)$, $\mathit{F}$ and $\mathit{V}$ are vectors denoting the rate of generation of new infections and transfer rates, respectively, gives

(24) $\mathit{F}=\left(\begin{array}{c}\mathit{p}{\pi }_h+{\lambda }_h{S}_h+q_0{\lambda }_h{S}_{\mathit{eh}}\\ 0\\ {\lambda }_v{S}_v\end{array}\right)$(24)

(25) $\mathit{V}=\left(\begin{array}{c}{q}_2{I}_h\\ -\mathit{\gamma }{I}_h+q_3{T}_h\\ u_2{I}_v\end{array}\right)$(25)

The Jacobian matrices F and V of $\mathit{F}$ and $\mathit{V}$ evaluated at the RDFE are, respectively:

(26) $\mathit{F}=\left(\begin{array}{ccc}0& 0& \frac{b{\beta }_h{S}_h^{\ast }}{N_h^{\ast }}+\frac{q_0\mathit{b}{\beta }_h{S}_{eh}^{\ast }}{N_h^{\ast }}\\ 0& 0& 0\\ \frac{b{\beta }_v{S}_v^{\ast }}{N_h^{\ast }}& \frac{rb{\beta }_v{S}_v^{\ast }}{N_h^{\ast }}& 0\end{array}\right)=\left(\begin{array}{ccc}0& 0& x_1\\ 0& 0& 0\\ x_2& \mathit{r}{x}_2& 0\end{array}\right)$(26)

(27) $\mathit{V}=\left(\begin{array}{ccc}{q}_2& 0& 0\\ -\mathit{\gamma }& q_3& 0\\ 0& 0& u_2\end{array}\right)$(27)

where $x_1=\frac{b{\beta }_h{S}_h^{\ast }}{N_h^{\ast }}$+$\frac{q_0\mathit{b}{\beta }_h{S}_{eh}^{\ast }}{N_h^{\ast }}$ and $x_2=\frac{b{\beta }_v{S}_v^{\ast }}{N_h^{\ast }}$

From the expression of V, the inverse of V is:

(28) $V^{-1}=\left(\begin{array}{ccc}\frac{1}{q_2}& 0& 0\\ \frac{\gamma }{q_2{q}_3}& \frac{1}{q_3}& 0\\ 0& 0& \frac{1}{u_2}\end{array}\right)$(28)

Hence, the next generation matrix $\mathit{F}{V}^{-1}$ is given by:

(29) $\mathit{F}{V}^{-1}=\left(\begin{array}{ccc}0& 0& x_1\\ 0& 0& 0\\ x_2& \mathit{r}{x}_2& 0\end{array}\right)\left(\begin{array}{ccc}\frac{1}{q_2}& 0& 0\\ \frac{\gamma }{q_2{q}_3}& \frac{1}{q_3}& 0\\ 0& 0& \frac{1}{u_2}\end{array}\right)$(29)

(30) $\mathit{F}{V}^{-1}=\left(\begin{array}{ccc}0& 0& \frac{x_1}{u_2}\\ 0& 0& 0\\ \frac{x_2}{q_2}+\frac{r\gamma x_2}{q_2{q}_3}& \frac{r{x}_2}{q_3}& 0\end{array}\right)=\left(\begin{array}{ccc}0& 0& k_1\\ 0& 0& 0\\ k_2& k_3& 0\end{array}\right)$(30)

(31) $\mathrm{where}{k}_1=\frac{x_1}{u_2}{k}_2=\frac{x_2}{q_2}+\frac{r\gamma x_2}{q_2{q}_3}{k}_3=\frac{r{x}_2}{q_3}$(31)

Using $\left|\mathit{F}{V}^{-1}-\mathit{\lambda I}\right|=0$, where I is a unit matrix and $\mathit{\lambda }$ an eigenvalue of $\mathit{F}{V}^{-1}$, we get the dominant eigenvalue as;

(32) $\mathit{\lambda }=\sqrt{\frac{b^2{\beta }_h{\beta }_v{\mu }_h\mathit{K}\left(1-\mathit{\epsilon }\right)\mathit{\psi }({\mu }_h+\mathit{\theta }{q}_0)(q_3+\mathit{r\gamma })}{{\pi }_h{q}_1{q}_2{q}_3{u}_2^2}\left(1-\frac{1}{\mathcal{N}}\right)}$(32)

Where $\mathcal{N}$ is a threshold quantity similar to the vector offspring number or net reproduction number used in [16,31]. Therefore, the reproductive number of the model is given by:

(33) $R_0=\sqrt{\frac{b^2{\beta }_h{\beta }_v{\mu }_h\mathit{K}\left(1-\mathit{\epsilon }\right)\mathit{\psi }({\mu }_h+\mathit{\theta }{q}_0)(q_3+\mathit{r\gamma })}{{\pi }_h{q}_1{q}_2{q}_3{u}_2^2}\left(1-\frac{1}{\mathcal{N}}\right)}=\sqrt{R_{0\mathit{h}}\times R_{0\mathit{v}}}$(33)

where

$R_{0\mathit{h}}=\frac{b{\beta }_h{\mu }_h({\mu }_h+\mathit{\theta }{q}_0)(q_3+\mathit{r\gamma })}{{\pi }_h{q}_1{q}_2{q}_3}\mathrm{and}{R}_{0\mathit{v}}=\frac{b{\beta }_v\mathit{K}\left(1-\mathit{\epsilon }\right)\mathit{\psi }}{u_2^2}\left(1-\frac{1}{\mathcal{N}}\right)$

It can be observed from equation (33)(33) $R_0=\sqrt{\frac{b^2{\beta }_h{\beta }_v{\mu }_h\mathit{K}\left(1-\mathit{\epsilon }\right)\mathit{\psi }({\mu }_h+\mathit{\theta }{q}_0)(q_3+\mathit{r\gamma })}{{\pi }_h{q}_1{q}_2{q}_3{u}_2^2}\left(1-\frac{1}{\mathcal{N}}\right)}=\sqrt{R_{0\mathit{h}}\times R_{0\mathit{v}}}$(33) that in the absence of educational campaigns ($\mathit{\theta }=0$) $R_0$ becomes, say

$R_{0\mathit{we}}=\sqrt{\frac{b^2{\beta }_h{\beta }_v{\mu }_h\mathit{K}\left(1-\mathit{\epsilon }\right)\mathit{\psi }(q_3+\mathit{r\gamma })}{{\pi }_h{q}_2{q}_3{u}_2^2}\left(1-\frac{1}{\mathcal{N}}\right)}$

The threshold quantities $R_{0\mathit{h}}$ and $R_{0\mathit{v}}$ represent the contributions of onchocerciasis disease spread from human to black fly (host to vector) and from black fly to human (vector to host), respectively. $R_{0\mathit{h}}$ represents the number of secondary cases of black flies (vectors) one infectious human will generate in a susceptible population of black flies during its infectious phase. Similarly, $R_{0\mathit{v}}$ can be interpreted as the number of secondary human cases generated by an infected black fly in an entirely susceptible human population over the course of its life time as infectious [32].

Stability of onchocerciasis-free equilibrium

Local stability of onchocerciasis-free equilibrium

Lemma 1:

Let M be a Metzler matrix, then $\mathit{S}(\mathit{M})<0$ if and only if M is invertible and $-M^{-1}\ge 0$, where $\mathit{S}(\mathit{M})=sup\{\mathit{Re\lambda },\mathit{\lambda }=\mathrm{eigenvalue}\mathrm{of}\mathit{M}\}$ is called the spectral bound of M [33].

Theorem 4:

The realistic disease-free equilibrium state

(34) ${\xi }_1=\left(\frac{{\pi }_h}{q_1},\frac{\theta {\pi }_h}{q_1{\mu }_h},0,0,\mathit{K}\left(1-\frac{1}{\mathcal{N}}\right),\frac{\mathit{K}\left(1-\mathit{\epsilon }\right)\psi }{u_2}\left(1-\frac{1}{\mathcal{N}}\right),0\right)\mathrm{with}\mathcal{N}>1$(34)

is locally asymptotically stable (LAS) if $R_0<1$ and unstable if $R_0>1$, where $R_0=\mathit{\rho }(\mathit{F}{V}^{-1})$ with F and V defined as in the previous sections

Proof: $\mathit{\rho }(\mathit{F}{V}^{-1})<1\Rightarrow \mathit{I}-\mathit{F}{V}^{-1}$ is an M-matrix [16,34]. Now $\mathit{I}-\mathit{F}{V}^{-1}$ being an M-matrix means that $-(\mathit{I}-\mathit{F}{V}^{-1})$ is a Metzler matrix and thus, is stable when the matrix $-[-(\mathit{I}-\mathit{F}{V}^{-1}){]}^{-1}\ge 0$

(35) $\mathit{\hspace{0.17em}}\mathrm{Let}\mathrm{M}=-\left(\mathit{I}-\mathit{F}{V}^{-1}\right)=-\left[\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)-\left(\begin{array}{ccc}0& 0& k_1\\ 0& 0& 0\\ k_2& k_3& 0\end{array}\right)\right]=\left(\begin{array}{ccc}-1& 0& k_1\\ 0& -1& 0\\ k_2& k_3& -1\end{array}\right)$(35)

where $k_1,k_2$ and $k_3$ are as defined before.

Let det $\mathrm{M}$ denotes the determinant of $\mathrm{M}$, then det$\mathrm{M}=k_1{k}_2-1=R_0^2-1$. Thus, $\mathrm{M}$ is invertible if $R_0^2-1\ne 0$.

Now, suppose $R_0^2-1\ne 0$, then $-M^{-1}$ is given by:

(36) $-M^{-1}=\left(\begin{array}{ccc}\frac{1}{1-R_0^2}& \frac{k_1{k}_3}{1-R_0^2}& \frac{k_1}{1-R_0^2}\\ 0& 1& 0\\ \frac{k_2}{1-R_0^2}& \frac{k_1{k}_3}{1-R_0^2}& \frac{k_1}{1-R_0^2}\end{array}\right)$(36)

But $k_i>0$ $(\mathit{i}=1,2,3)$ whenever $\mathcal{N}>1$. Hence, $-M^{-1}\ge 0$ if $R_0<1$. Therefore, the realistic disease-free equilibrium state ${\xi }_1$ is locally asymptotically stable if $R_0<1$ and unstable if $R_0>1$.

Global stability of onchocerciasis-free equilibrium

Following [35,36] the global asymptotic stability of a system equilibrium point can be established by first expressing the system in the form:

(37) $\left\{\begin{array}{c}\frac{d{Y}_s}{\mathit{dt}}=B_1\left(Y_s-Y_{\mathit{RDFE}}\right)+B_{12}{Y}_i\\ \frac{d{Y}_i}{\mathit{dt}}=B_2{Y}_i\end{array}\right.$(37)

Here, $Y_s$ and $Y_i$ denotes the compartments of non-transmitting hosts and vectors, respectively, with $Y_s={\left(S_h,S_{\mathit{eh}},A_v,S_v\right)}^{\mathit{T}}$

(38) $Y_i={\left(I_h,T_h,I_v\right)}^{\mathit{T}}{Y}_{\mathit{RDFE}}=(S_h^{\ast },S_{eh}^{\ast },A_v^{\ast },S_v^{\ast })$(38)

(39) $B_1=\frac{\mathrm{\partial }{Y}_s}{\mathrm{\partial }(S_h,S_{\mathit{eh}},A_v,S_v)}$(39)

(40) $B_{12}=\frac{\mathrm{\partial }{Y}_s}{\mathrm{\partial }(I_h,T_h,I_v)}$(40)

(41) $B_2=\frac{\mathrm{\partial }{Y}_i}{\mathrm{\partial }(I_h,T_h,I_v)}$(41)

Using our model system of equations, we get:

(42) $B_1=\left(\begin{array}{cccc}-q_1& 0& 0& 0\\ \mathit{\theta }& -{\mu }_h& 0& 0\\ 0& 0& -\mathit{d}& \frac{{\pi }_v}{\mathcal{N}}\\ 0& 0& \left(1-\mathit{\epsilon }\right)\mathit{\psi }& -u_2\end{array}\right)$(42)

where $\mathit{d}=\left(1-\mathit{\epsilon }\right)\mathit{\psi }+u_1+\frac{{\pi }_v\left(1-\mathit{\epsilon }\right)\mathit{\psi }}{u_2}\left(1-\frac{1}{\mathcal{N}}\right)$

(43) $B_{12}=\left(\begin{array}{cccc}0& 0& -\frac{b{\beta }_h{S}_h^{\ast }}{N_h^{\ast }}& 0\\ 0& \mathit{\phi }& -\frac{q_0\mathit{b}{\beta }_h{S}_h^{\ast }}{N_h^{\ast }}& 0\\ 0& 0& {\pi }_v\left(1-\frac{A_v^{\ast }}{\mathit{K}}\right)& 0\\ -\frac{b{\beta }_v{S}_v^{\ast }}{N_h^{\ast }}& -\frac{rb{\beta }_v{S}_v^{\ast }}{N_h^{\ast }}& 0& 0\end{array}\right)$(43)

(44) $B_2=\left(\begin{array}{ccc}-q_2& 0& l_1\\ \mathit{\gamma }& -q_3& 0\\ l_2& \mathit{r}{l}_2& -u_2\end{array}\right)$(44)

where;

(45) $l_1=\frac{b{\beta }_h\left({\mu }_h+\mathit{\theta }{q}_0\right)}{q_1}$(45)

(46) $l_2=\frac{b{\beta }_v{\mu }_h\mathit{K}\left(1-\mathit{\epsilon }\right)\mathit{\psi }}{u_2{\pi }_h}\left(1-\frac{1}{\mathcal{N}}\right)$(46)

From the above we formulate the theorem as follows.

Theorem 5:

The system $\frac{d{Y}_s}{\mathit{dt}}=B_1\left(Y_s-Y_{\mathit{RDFE}}\right)+B_{12}{Y}_i$ is globally asymptotically stable at the RDFE when all eigenvalues of matrix $B_1$ have negative real parts and $B_2$ is a Metzler matrix.

Proof: Clearly, two eigenvalues of the matrix $B_1$ are ${\lambda }_1=-q_1$ and ${\lambda }_2=-{\mu }_h$. The remaining two eigenvalues are obtained from the sub-matrix:

(47) $\mathit{A}=\left(\begin{array}{cc}-\mathit{d}& \frac{{\pi }_v}{\mathcal{N}}\\ (1-\mathit{\epsilon })\mathit{\psi }& -u_2\end{array}\right)$(47)

The characteristic equation of the matrix in 47 is

(48) ${\lambda }^2+(u_2+\mathit{d})\mathit{\lambda }+{\pi }_v\left(1-\mathit{\epsilon }\right)\mathit{\psi }\left(1-\frac{1}{\mathcal{N}}\right)=0$(48)

Since in equation (48)(48) ${\lambda }^2+(u_2+\mathit{d})\mathit{\lambda }+{\pi }_v\left(1-\mathit{\epsilon }\right)\mathit{\psi }\left(1-\frac{1}{\mathcal{N}}\right)=0$(48) , $u_2+\mathit{d}>0$ and ${\pi }_v\left(1-\mathit{\epsilon }\right)\mathit{\psi }\left(1-\frac{1}{\mathcal{N}}\right)>0$ whenever $\mathcal{N}>1$, we conclude using the Routh-Hurwitz stability criterion, that the eigenvalues ${\lambda }_3$ and ${\lambda }_4$ have negative real parts. Hence, all the eigenvalues of the matrix $B_1$ have negative real parts.

Also,

(49) $B_2=\left(\begin{array}{ccc}-q_2& 0& l_1\\ \mathit{\gamma }& -q_3& 0\\ l_2& \mathit{r}{l}_2& -u_2\end{array}\right)$(49)

is a Metzler matrix (since all the off diagonal entries are non negative). Thus, the system

(50) $\frac{d{Y}_s}{\mathit{dt}}=B_1\left(Y_s-Y_{\mathit{RDFE}}\right)+B_{12}{Y}_i$(50)

is globally asymptotically stable at the realistic disease-free equilibrium.

Onchocerciasis endemic equilibrium

Let $(S_h^{\ast \ast },S_{eh}^{\ast \ast },I_h^{\ast \ast },T_h^{\ast \ast },A_v^{\ast \ast },S_v^{\ast \ast },I_v^{\ast \ast })$ be the endemic equilibrium point for the onchocerciasis model, then solving the system:

$\left(1-\mathit{p}\right){\pi }_h-\left({\lambda }_h+q_1\right)S_h=0$

$\mathit{\theta }{S}_h+\mathit{\phi }{T}_h-\left(q_0{\lambda }_h+{\mu }_h\right)S_{\mathit{eh}}=0$

$\mathit{p}{\pi }_h+{\lambda }_h{S}_h+q_0{\lambda }_h{S}_{\mathit{eh}}-q_2{I}_h=0$

$\mathit{\gamma }{I}_h-q_3{T}_h=0$

${\pi }_v\left(1-\frac{A_v}{\mathit{K}}\right)\left(S_v+I_v\right)-\left[\left(1-\mathit{\epsilon }\right)\mathit{\psi }+u_1\right]A_v=0$

$\left(1-\mathit{\epsilon }\right)\mathit{\psi }{A}_v-({\lambda }_v+u_2)S_v=0$

${\lambda }_v{S}_v-u_2{I}_v=0$

The following solutions are obtained

(51) $S_h^{\ast \ast }=\frac{\left(1-\mathit{p}\right){\pi }_h}{({\lambda }_h^{\ast \ast }+q_1)}$(51)

(52) $S_{eh}^{\ast \ast }=\frac{\theta S_h^{\ast \ast }+\mathit{\phi }{T}_h^{\ast \ast }}{q_0{\lambda }_h^{\ast \ast }+{\mu }_h}$(52)

(53) $I_h^{\ast \ast }=\frac{p{\pi }_h+{\lambda }_h^{\ast \ast }{S}_h^{\ast \ast }+q_0{\lambda }_h^{\ast \ast }{S}_{eh}^{\ast \ast }}{q_2}$(53)

(54) $T_h^{\ast \ast }=\frac{\gamma I_h^{\ast \ast }}{q_3}$(54)

(55) $A_v^{\ast \ast }=0\mathrm{or}\mathit{K}\left(1-\frac{1}{\mathcal{N}}\right)$(55)

(56) $S_v^{\ast \ast }=\frac{\left(1-\epsilon \right)\psi }{{\lambda }_v^{\ast \ast }+u_2}{A}_v^{\ast \ast }$(56)

(57) $I_v^{\ast \ast }=\frac{{\lambda }_v^{\ast \ast }}{u_2}{S}_v^{\ast \ast }=\frac{{\lambda }_v^{\ast \ast }\left(1-\mathit{\epsilon }\right)\mathit{\psi }}{u_2({\lambda }_v^{\ast \ast }+u_2)}{A}_v^{\ast \ast }$(57)

Now, $A_v^{\ast \ast }=0$ yields the endemic equilibrium

(58) ${\xi }_2=\left(\frac{(1-p){\pi }_h}{q_1},\frac{q_2{q}_3\mathit{\theta }\left(1-\mathit{p}\right){\pi }_h+\mathit{p}{q}_1\mathit{\phi \gamma }{\pi }_h}{q_1{q}_2{q}_3{\mu }_h},\frac{p{\pi }_h}{q_2},\frac{p\gamma {\pi }_h}{q_2{q}_3}0,0,0\right)$(58)

Clearly, when the inflow of infected immigrants is zero, that is $\mathit{p}=0$, ${\xi }_2$ is the same as the trivial disease-free equilibrium $({\xi }_0)$, otherwise there is no trivial disease-free equilibrium [37,38].

Using equation 53 and the forces of infections;

(59) ${\lambda }_h^{\ast \ast }=\frac{b{\beta }_h{I}_v^{\ast \ast }}{N_h^{\ast \ast }}$(59)

and

(60) ${\lambda }_v^{\ast \ast }=\frac{b{\beta }_v(I_h^{\ast \ast }+\mathit{r}{T}_h^{\ast \ast })}{N_h^{\ast \ast }}$(60)

gives:

(61) $\mathit{f}({\lambda }_h^{\ast \ast })=a_0{\lambda }_h^{\ast \ast 3}+a_1{\lambda }_h^{\ast \ast 2}+a_2{\lambda }_h^{\ast \ast }+a_3=0$(61)

where

(62) $a_0=q_0\left[\frac{u_2\left(q_2{q}_3-\mathit{\gamma \phi }\right)+\mathit{b}{\beta }_v{\mu }_h(q_3+\mathit{r\gamma })}{q_2{q}_3{u}_2}\right]$(62)

(63) $a_1=q_0{q}_1\left(g_1-R_{0we}^2\right)$(63)

(64) $g_1=\frac{\begin{array}{c}b{\beta }_v{\mu }_h(q_3+\mathit{r\gamma })[{\mu }_h+q_0(\mathit{p}{q}_1+\mathit{\theta }(1-\mathit{p}))]\\ +q_2{q}_3{u}_2(q_0{q}_1+{\mu }_h)-q_0{q}_1{u}_2\mathit{\gamma \phi }\end{array}}{q_0{q}_1{q}_2{q}_3{u}_2}$(64)

(65) $a_2=q_1{\mu }_h\left[\mathit{p}{g}_2+1-\frac{\begin{array}{c}{b}^2{\beta }_h{\beta }_v{\mu }_h\mathit{K}(1-\mathit{\epsilon })\mathit{\psi }(1-\frac{1}{N})(q_3+\mathit{r\gamma })\\ [{\mu }_h+q_0(\mathit{p}{q}_1+\mathit{\theta }(1-\mathit{p}))\end{array}}{{\pi }_h{q}_1{q}_2{q}_3{u}_2^2}\right]$(65)

(66) $g_2=\frac{b{\beta }_v{\mu }_h(q_3+\mathit{r\gamma })}{{\pi }_h{q}_2{u}_2}$(66)

(67) $a_3=-\mathit{p}{q}_1{\mu }_h{R}_{0we}^2$(67)

It is easy to see from equation (61)(61) $\mathit{f}({\lambda }_h^{\ast \ast })=a_0{\lambda }_h^{\ast \ast 3}+a_1{\lambda }_h^{\ast \ast 2}+a_2{\lambda }_h^{\ast \ast }+a_3=0$(61) that

$\mathit{f}(0)=a_3<0\mathrm{and}\underset{{\lambda }_h^{\ast \ast }\to +\mathrm{\infty }}{lim}\mathit{f}({\lambda }_h^{\ast \ast })=+\mathrm{\infty }$

This implies that there is a change of sign of the function $\mathit{f}\left({\lambda }_h^{\ast \ast }\right)$ on the interval $[0,+\mathrm{\infty })$, hence, $\mathit{f}\left({\lambda }_h^{\ast \ast }\right)=0$ has a root lying in $[0,+\mathrm{\infty })$. Thus, the biological meaning of $\mathit{f}\left({\lambda }_h^{\ast \ast }\right)=0$ is guaranteed. Next, we apply the Descartes Rule of Sign Change to explore on the number of endemic solutions (see Table 5).

Table 5. Number of possible positive roots of $\mathit{f}({\lambda }_h^{\ast \ast })$.

Case	$a_0$	$a_1$	$a_2$	$a_3$	Sign change	+ve roots
i	+	+	+	$-$	1	0, 1
ii	+	+	$-$	$-$	1	0, 1
iii	+	$-$	+	$-$	3	1, 3
iv	+	$-$	$-$	$-$	1	0, 1

From Table 5, we state and prove the following theorem.

Theorem 6:

If $a_1<0$ and $a_2>0$, system (1) has three distinct endemic equilibrium.Proof:

(68) $\mathit{f}\left({\lambda }_h^{\ast \ast }\right)=a_0{\lambda }_h^{\ast \ast 3}+a_1{\lambda }_h^{\ast \ast 2}+a_2{\lambda }_h^{\ast \ast }+a_3=0$(68)

(69) $\mathit{f}{ }^{\mathrm{\prime }}\left({\lambda }_h^{\ast \ast }\right)=3a_0{\lambda }_h^{\ast \ast 2}+2a_1{\lambda }_h^{\ast \ast }+a_2$(69)

Now;

(70) $\mathit{f}{ }^{\mathrm{\prime }}\left({\lambda }_h^{\ast \ast }\right)=0$(70)

(71) ${\lambda }_h^{\ast \ast }=\frac{-a_1\pm \sqrt{a_1^2-3a_0{a}_2}}{3a_0}$(71)

Clearly, ${\lambda }_h^{\ast \ast }$ is real and positive if $a_1<0$ and $a_2>0$. Thus, the solution ${\lambda }_h^{\ast \ast }$ is positive implies $\mathit{f}{ }^{\mathrm{\prime }}\left({\lambda }_h^{\ast \ast }\right)=0$ has two positive solutions. Hence, it follows from the Fundamental Theorem of Algebra that the endemic equation $\mathit{f}\left({\lambda }_h^{\ast \ast }\right)=0$ has three positive solutions if $a_1<0$ and $a_2>0$.

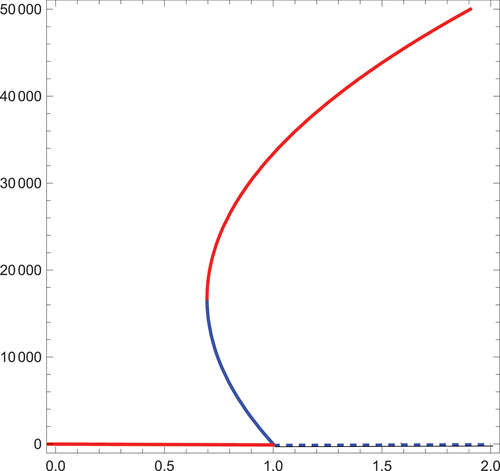
Multiple endemic equilibrium and backward bifurcation

The phenomenon of backward bifurcation is often experienced when a stable disease-free equilibrium coexist with a stable endemic equilibrium. This phenomenon is common with epidemiological models with multiple roots of transmission. Here, if the existence of multiple endemic equilibrium coincide with $R_0<1$, then our model undergoes backward bifurcation as shown in Figure 3. The occurrence of backward bifurcation implies that the idea of $R_0<1$ its a necessary but not a sufficient condition for eradication of the disease [39].

Figure 3. Backward bifurcation.

Endemic condition in the absence of infected immigrants (p = 0)

It is easy to see that when $\mathit{p}=0$, equation (61)(61) $\mathit{f}({\lambda }_h^{\ast \ast })=a_0{\lambda }_h^{\ast \ast 3}+a_1{\lambda }_h^{\ast \ast 2}+a_2{\lambda }_h^{\ast \ast }+a_3=0$(61) becomes:

(72) $a_0{\lambda }_h^{\ast \ast 3}+a_1{\lambda }_h^{\ast \ast 2}+a_2{\lambda }_h^{\ast \ast }=0$(72)

(73) $\Rightarrow {\lambda }_h^{\ast \ast }=0\mathrm{or}{b}_0{\lambda }_h^{\ast \ast 2}+b_1{\lambda }_h^{\ast \ast }+b_2=0$(73)

where:

$\begin{array}{cc}{b}_0& =a_0{b}_1=q_0{q}_1\left(g_3-R_{0we}^2\right)b_2=q_1{\mu }_h\left(1-R_0^2\right)\\ g_3& =\frac{b{\beta }_v{\mu }_h(q_3+\mathit{r\gamma })({\mu }_h+\mathit{\theta }{q}_0)+q_2{q}_3{u}_2(q_0{q}_1+{\mu }_h)-q_0{q}_1{u}_2\mathit{\gamma \phi }}{q_0{q}_1{q}_2{q}_3{u}_2}\end{array}$

Next, we explore the conditions for the existence of positive roots for

(74) $b_0{\lambda }_h^{\ast \ast 2}+b_1{\lambda }_h^{\ast \ast }+b_2=0$(74)

Since $b_0=a_0>0$, the number and nature of roots of equation (74)(74) $b_0{\lambda }_h^{\ast \ast 2}+b_1{\lambda }_h^{\ast \ast }+b_2=0$(74) depends on the value of $R_0$ and the sign of discriminant $\mathrm{\Delta }=b_1^2-4b_0{b}_2$. Thus, the following theorem is elaborated.

Theorem 7:

In the absence of infected immigrants then;

1. For $R_0>1$, system 3 admits a unique endemic equilibrium point

2. For $b_1<0$ and $b_2=0$ or $b_1^2-4b_0{b}_2=0$, system 3 has a unique endemic equilibrium point

3. For $R_0<1,b_1<0$ and $b_1^2-4b_0{b}_2>0$, system 3 has two endemic equilibrium points

4. Otherwise, system 3 has no endemic equilibrium point

Theorem 7 case (iii) suggests that in the absence of importation of infections, the model exhibits backward bifurcation. This is depicted in Figure 3 below. The occurrence of backward bifurcation means that even in the absence of importation of infections, $R_0<1$ is not enough for the eradication of onchocerciasis.

Global stability of the unique endemic equilibrium point

It has been established in theorem 7 that in the absence of inflow of infective immigrants, system 3 has a unique endemic equilibrium point if $R_0>1$. In what follows, we establish the global stability of this unique endemic equilibrium.

Lema 2: In the absence of importation of infections, the unique endemic equilibrium point of system 3 is globally asymptotically stable (GAS) at the interior of the model invariant region if $R_0>1$ and unstable otherwise.

Proof: Consider the Lyapunov function:

$\begin{array}{rl}& \mathit{L}\left(S_h^{\ast \ast },S_{eh}^{\ast \ast },I_h^{\ast \ast },T_h^{\ast \ast },A_v^{\ast \ast },S_v^{\ast \ast },I_v^{\ast \ast }\right)\\ & =\left(S_h-S_h^{\ast \ast }-S_h^{\ast \ast }ln\frac{S_h^{\ast \ast }}{S_h}\right)+\left(S_{\mathit{eh}}-S_{eh}^{\ast \ast }-S_{eh}^{\ast \ast }ln\frac{S_{eh}^{\ast \ast }}{S_{\mathit{eh}}}\right)\\ & +\left(I_h-I_h^{\ast \ast }-I_h^{\ast \ast }ln\frac{I_h^{\ast \ast }}{I_h}\right)+\left(T_h-T_h^{\ast \ast }-T_h^{\ast \ast }ln\frac{T_h^{\ast \ast }}{T_h}\right)\\ & +\left(A_v-A_v^{\ast \ast }-A_v^{\ast \ast }ln\frac{A_v^{\ast \ast }}{A_v}\right)+\left(S_v-S_v^{\ast \ast }-S_v^{\ast \ast }ln\frac{S_v^{\ast \ast }}{S_v}\right)\\ & +\left(I_v-I_v^{\ast \ast }-I_v^{\ast \ast }ln\frac{I_v^{\ast \ast }}{I_v}\right)\end{array}$

Taking the time derivative of L gives:

$\begin{array}{l}\frac{\mathit{dL}}{\mathit{dt}}=\left(1-\frac{S_h^{**}}{S_h}\right)\frac{d{S}_h}{\mathit{dt}}+\left(1-\frac{S_{eh}^{**}}{S_{\mathit{eh}}}\right)\frac{\mathit{d}{\mathit{S}}_{\mathit{eh}}}{\mathit{dt}}\\ +\left(1-\frac{I_h^{**}}{I_h}\right)\frac{d{I}_h}{\mathit{dt}}\\ +\left(1-\frac{T_h^{**}}{T_h}\right)\frac{d{T}_h}{\mathit{dt}}+\left(1-\frac{A_v^{**}}{A_v}\right)\frac{d{A}_v}{\mathit{dt}}\\ +\left(1-\frac{S_v^{**}}{S_v}\right)\frac{d{S}_v}{\mathit{dt}}+\left(1-\frac{I_v^{**}}{I_v}\right)\frac{d{I}_v}{\mathit{dt}}\\ =\left(1-\frac{S_h^{**}}{S_h}\right)[(1-\mathit{p}){\pi }_h-({\lambda }_h+q_1)S_h]+\left(1-\frac{S_{eh}^{**}}{S_{\mathit{eh}}}\right)\\ \left[\mathit{\theta }{S}_h+\mathit{\phi }{T}_h-(q_0{\lambda }_h+{\mu }_h)S_{\mathit{eh}}\right]+\left(1-\frac{I_h^{**}}{I_h}\right)\\ \left(\mathit{p}{\pi }_h+{\lambda }_h{S}_h+q_0{\lambda }_h{S}_{\mathit{eh}}-q_2{I}_h\right)+\left(1-\frac{T_h^{**}}{T_h}\right)\\ \left(\mathit{\gamma }{I}_h-q_3{T}_h\right)\\ +\left(1-\frac{A_v^{**}}{A_v}\right)[{\pi }_v\left(1-\frac{A_v}{\mathit{K}}\right)\left(S_v+I_v\right)\\ -\left[\left(1-\mathit{\epsilon }\right)\mathit{\psi }+u_1]\mathit{Av}\right]\\ +\left(1-\frac{S_v^{**}}{S_v}\right)\left[\left(1-\mathit{\epsilon }\right)\mathit{\psi }{A}_v-({\lambda }_v+u_2)S_v\right]\\ +\left(1-\frac{I_v^{**}}{I_v}\right)\left({\lambda }_v{S}_v-u_2{I}_v\right)={\pi }_h+({\lambda }_h+q_1)S_h^{**}\end{array}$

$\begin{array}{rl}& +\mathit{p}{\pi }_h\frac{S_h^{\ast \ast }}{S_h}-({\lambda }_h+q_1)S_h-{\pi }_h\frac{S_h^{\ast \ast }}{S_h}+\mathit{\theta }{S}_h\\ & +\mathit{\phi }{T}_h+(q_0{\lambda }_h+{\mu }_h)S_{eh}^{\ast \ast }-(q_0{\lambda }_h+{\mu }_h)S_{\mathit{eh}}\\ & -\mathit{\theta }{S}_h\frac{S_{eh}^{\ast \ast }}{S_{\mathit{eh}}}-\mathit{\phi }{T}_h\frac{S_{eh}^{\ast \ast }}{S_{\mathit{eh}}}+{\lambda }_h{S}_h\\ & +q_0{\lambda }_h{S}_{\mathit{eh}}+q_2{I}_h^{\ast \ast }-q_2{I}_h-\mathit{p}{\pi }_h\frac{I_h^{\ast \ast }}{I_h}-{\lambda }_h{S}_h\frac{I_h^{\ast \ast }}{I_h}\\ & -q_0{\lambda }_h{S}_{\mathit{eh}}\frac{I_h^{\ast \ast }}{I_h}+\mathit{\gamma }{I}_h+q_3{T}_h^{\ast \ast }-\mathit{\gamma }{I}_h\frac{T_h^{\ast \ast }}{T_h}-q_3{T}_h\\ & +N_{\mathit{mv}}{\pi }_v+N_{\mathit{mv}}{\pi }_v\frac{A_v^{\ast \ast }}{\mathit{K}}+[(1-\mathit{\epsilon })\mathit{\psi }+u_1]A_v^{\ast \ast }\\ & -N_{\mathit{mv}}{\pi }_v\frac{A_v}{\mathit{K}}-u_1{A}_v-N_{\mathit{mv}}{\pi }_v\frac{A_v^{\ast \ast }}{A_v}+{\lambda }_v{S}_v^{\ast \ast }\\ & +u_2{S}_v^{\ast \ast }-u_2{S}_v-(1-\mathit{\epsilon })\mathit{\psi }{A}_v\frac{S_v^{\ast \ast }}{S_v}+u_2{I}_v^{\ast \ast }\\ & -u_2{I}_v-{\lambda }_v{S}_v\frac{I_v^{\ast \ast }}{I_v}=L^{+}-L^{-}\\ & \mathrm{where}\\ & L^{+}={\pi }_h+({\lambda }_h+q_1)S_h^{\ast \ast }+\mathit{p}{\pi }_h\frac{S_h^{\ast \ast }}{S_h}\\ & +\mathit{\theta }{S}_h+\mathit{\phi }{T}_h+(q_0{\lambda }_h+{\mu }_h)S_{eh}^{\ast \ast }+{\lambda }_h{S}_h+q_0{\lambda }_h{S}_{\mathit{eh}}\\ & +q_2{I}_h^{\ast \ast }+\mathit{\gamma }{I}_h+q_3{T}_h^{\ast \ast }+N_{\mathit{mv}}{\pi }_v+N_{\mathit{mv}}{\pi }_v\frac{A_v^{\ast \ast }}{\mathit{K}}\\ & +[(1-\mathit{\epsilon })\mathit{\psi }+u_1]A_v^{\ast \ast }+{\lambda }_v{S}_v^{\ast \ast }+u_2{S}_v^{\ast \ast }+u_2{I}_v^{\ast \ast }{L}^{-}\\ & =({\lambda }_h+q_1)S_h+{\pi }_h\frac{S_h^{\ast \ast }}{S_h}+(q_0{\lambda }_h+{\mu }_h)S_{\mathit{eh}}\\ & +\mathit{\theta }{S}_h\frac{S_{eh}^{\ast \ast }}{S_{\mathit{eh}}}+\mathit{\phi }{T}_h\frac{S_{eh}^{\ast \ast }}{S_{\mathit{eh}}}+q_2{I}_h+\mathit{p}{\pi }_h\frac{I_h^{\ast \ast }}{I_h}+{\lambda }_h{S}_h\frac{I_h^{\ast \ast }}{I_h}\\ & +q_0{\lambda }_h{S}_{\mathit{eh}}\frac{I_h^{\ast \ast }}{I_h}+\mathit{\gamma }{I}_h\frac{T_h^{\ast \ast }}{T_h}+q_3{T}_h+N_{\mathit{mv}}{\pi }_v\frac{A_v}{\mathit{K}}+\\ & u_1{A}_v+N_{\mathit{mv}}{\pi }_v\frac{A_v^{\ast \ast }}{A_v}+(1-\mathit{\epsilon })\mathit{\psi }{A}_v\frac{S_v^{\ast \ast }}{S_v}+u_2{I}_v+{\lambda }_v{S}_v\frac{I_v^{\ast \ast }}{I_v}\end{array}$

$\frac{\mathit{dL}}{\mathit{dt}}<0\mathrm{if}{L}^{+}<L^{-}$

Also, $\frac{\mathit{dL}}{\mathit{dt}}=0\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{S}_h^{\ast \ast }=S_h,S_{eh}^{\ast \ast }=S_{\mathit{eh}},I_h^{\ast \ast }=I_h,T_h^{\ast \ast }=T_h,A_v^{\ast \ast }=A_v,S_v^{\ast \ast }=S_v,\mathrm{and}{I}_v^{\ast \ast }=I_v$

Therefore, the largest compact invariant set within the model’s invariant region is the singleton $\left(S_h^{\ast \ast },S_{eh}^{\ast \ast },I_h^{\ast \ast },T_h^{\ast \ast },A_v^{\ast \ast },S_v^{\ast \ast },I_v^{\ast \ast }\right)$. Hence, the unique endemic equilibrium is globally asymptotically stable if $L^{+}<L^{-}$ [24].

Sensitivity analysis

Sensitivity analysis is used to determine the parameters that mostly contribute to disease spread or increase $\left(R_0\right)$. These parameters should be targeted during any intervention aimed at combating the infection.

Sensitivity indices

Using the normalized forward sensitivity index relation;

(75) ${\Gamma }_x^w=\frac{\mathrm{\partial }\mathit{w}}{\mathrm{\partial x}}\times \frac{x}{w}$(75)

we obtain the values for sensitivity indices of the parameters of the reproductive number, $\left(R_0\right)$ as presented in Table 6.

Table 6. The values of the sensitivity indices.

Parameter	Sensitivity Index
b	$+1.00$
${\beta }_h$	$+0.50$
${\beta }_v$	$+0.50$
${\pi }_h$	$-0.50$
${\mu }_h$	$+0.49997$
${\pi }_v$	$+$3.6 x10^–3
$\mathit{k}$	$+0.50$
$\mathit{\theta }$	$-$1.84877x10^–5
$\mathit{\sigma }$	$-0.2143$
$\mathit{\gamma }$	$-0.471$
$\mathit{\phi }$	$-0.02852$
$\mathit{\epsilon }$	$-0.33495$
r	$+0.02853$
$\mathit{\psi }$	$+0.50243$
${\mu }_a$	$-$4.04995x10^–4
${\mu }_{\mathrm{\ell }}$	$-2$.02498x10^–3
${\mu }_t$	$-$0.028798
${\mu }_v$	$-$0.9748

If the sign of the sensitivity index of a given parameter of $R_0$ is positive, it means $R_0$ is directly proportional to that parameter. That is, an increase (decrease) in the parameter value when other parameters remain constant would result in an increase (decrease) in disease incidence.

Conversely, if the sign of the sensitivity index of a given parameter is negative, then $R_0$ is indirectly proportional to that parameter [40].

From Table 6, we see that the parameters b, ${\beta }_h$, ${\beta }_v$, ${\mu }_h$, K, ${\pi }_v$, r and $\mathit{\psi }$ are directly proportional to the disease spread $(R_0)$ while ${\pi }_h$, $\mathit{\theta }$, $\mathit{\sigma }$, $\mathit{\gamma }$, $\mathit{\phi }$, $\mathit{\epsilon }$, ${\mu }_a$, ${\mu }_l$, ${\mu }_t$ and ${\mu }_v$ are inversely proportional to $R_0$. Hence, the most sensitive parameter is Black fly biting rate, $(\mathit{b})$.

Numerical simulations

To demonstrate the robustness of the model, system 3 is simulated using the set of parameter values in Table 7. The initial conditions used in the simulations were as follows; $S_h\left(0\right)=600$, $I_h\left(0\right)=50$, $T_h\left(0\right)=0$, $A_v\left(0\right)=5,000$, $S_v\left(0\right)=1,000$, and $I_v\left(0\right)=30$.

Table 7. The model parameter values.

Parameter	Value/Range	Source
${\pi }_h$	0.031	[8]
${\mu }_h$	1/23178	[8]
${\beta }_h$	0.0114	[3]
$\mathit{\theta }$	0.5	[20]
$\mathit{\sigma }$	0.3	[20]
$\mathit{\gamma }$	0.65	[27]
$\mathit{\phi }$	0.0891	[9,12]
$\mathit{r}$	0.0083	[27]
${\pi }_v$	600	[27]
$\mathit{K}$	6000	[20,27]
$\mathit{b}$	0.0855	[8]
${\beta }_v$	0.0111	[3]
$\mathit{\psi }$	1.926	[20]
$\mathit{\epsilon }$	0.4	[20]
${\mu }_v$	1.354	[27]
$\mathit{\mu }\mathit{a}$	2	[20]
${\mu }_{\mathrm{\ell }}$	0.4	[20]
$\mathit{\mu }\mathit{t}$	0–0.9	[8]

The graphical solutions and their interpretations are presented in Figures 4–12.

Figure 4. Susceptible human class with controls.

Figure 5. Susceptible educated human class with controls.

Figure 6. Infected human class with controls.

Figure 7. Treated human class with controls.

Figure 8. Aquatic vector class with controls.

Figure 9. Susceptible vector class with controls.

Figure 10. Infected vector class with controls.

Figure 11. Infected human class without infected immigrants.

Figure 12. Infected vector class without infected immigrants.

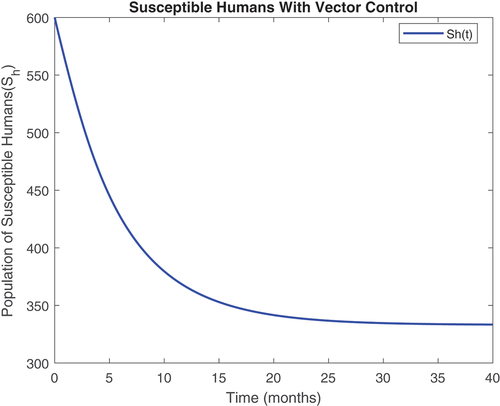
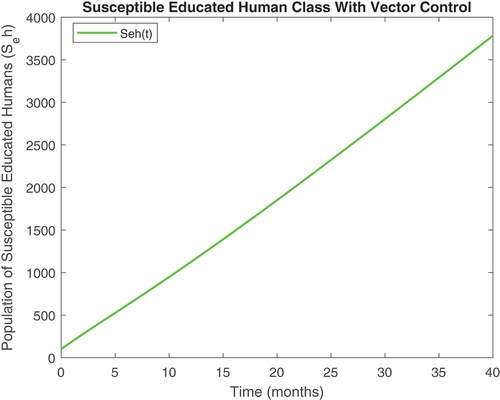
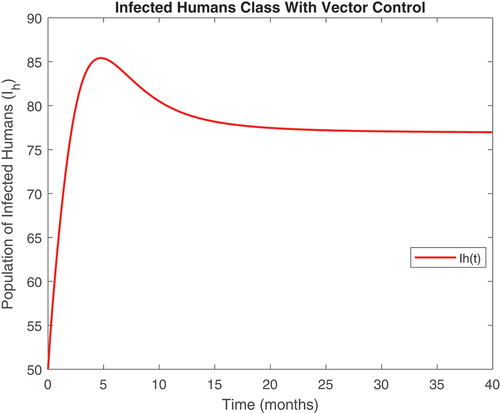
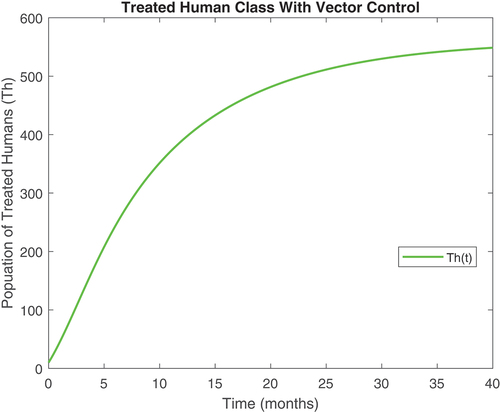
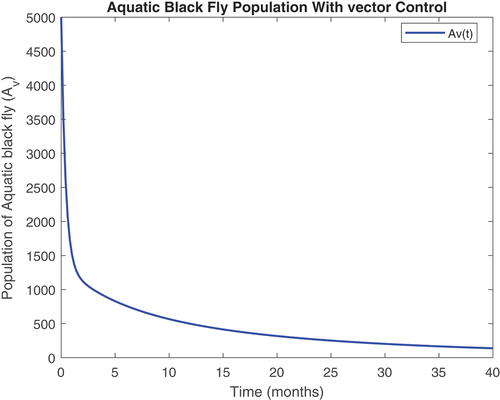
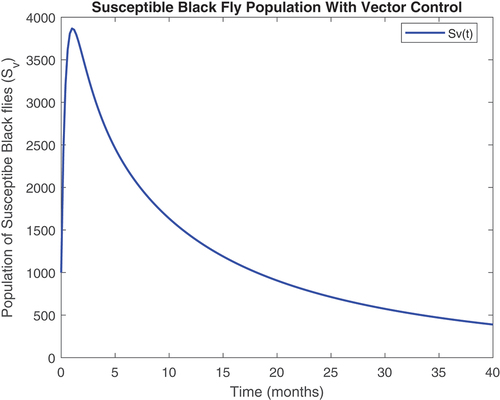
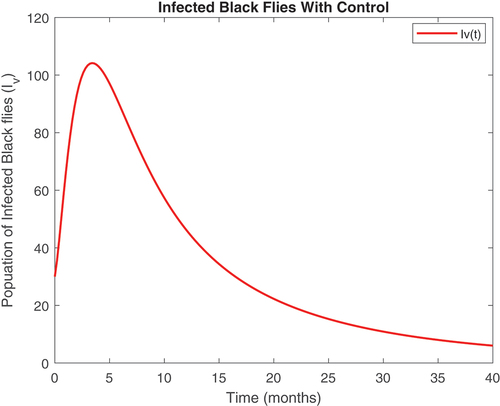
Figures 4–9 revealed that onchocerciasis disease continue to persist even with control measures in place. This is an indication that these controls need to be revised. The biological implication of Figure 4 is that as the susceptible population become infected, the infectious population keeps increasing. Hence, the susceptible population reduce steadily. This may be caused by the inflow of infectious immigrants. Moreover, from Figures 8–10, one can see that the vector control are very effective at reducing vector numbers. Control incorporated in combating the vector populations are encouraged since this control measure is efficient.

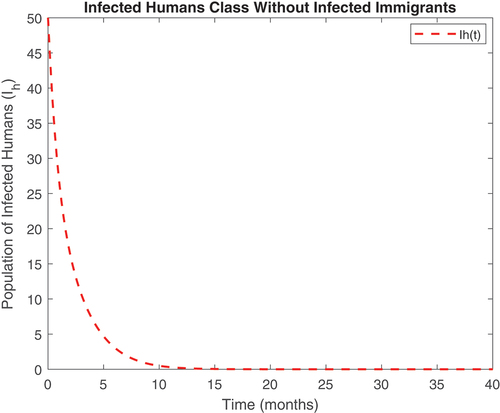
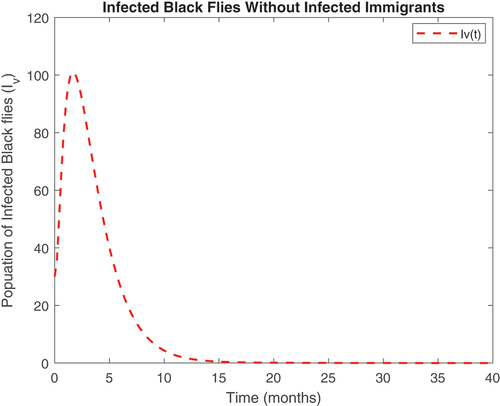
Also, Figures 11 and 12 displayed the evolution of onchocerciasis disease in the human and black fly populations in the absence of infected immigrants, respectively. These two graphs indicate that onchocerciasis can be eradicated if the importation of infections is properly monitored. Therefore, proper monitoring and evaluation of black fly population should be encouraged.

Conclusion

In this study, we developed and analyzed a mathematical model that explains the infection dynamics, control and eradication of human onchocerciasis disease in a community where humans (hosts) and black flies (vectors) interact. The model considered influence of education policy, vector control measures and the inflow of infected immigrants on the spread of the disease.

Our analysis showed that the model has two trivial equilibria; one at the disease-free equilibrium state and the other at disease persistence equilibrium point. It was further observed that these trivial solutions were the same in the absence of imported infections. The model also exhibited a biologically desired disease-free steady state or realistic disease-free equilibrium (RDFE) whenever the black fly reproduction number is greater than one.

Using stability theorems of Metzler matrices and the Routh-Hurwitz stability criterion, we proved that the biologically desired infection-free equilibrium point is both locally and globally asymptotically stable when the disease reproduction number $(R_0)$ is less than one and unstable if $R_0>1$. We demonstrated that the model may admit three distinct endemic equilibrium states. Furthermore, we established that in the absence of importation of infections, the model will undergo backward bifurcation when $R_0<1$ or may admit a unique endemic equilibrium if $R_0>1$.

The results from the sensitivity analysis revealed that the black fly biting and removal rates ($\mathit{b}\mathrm{and}{\mu }_h$) were mostly sensitive to the disease spread. It was also revealed that the black fly biting and removal rates $\mathit{b}\mathrm{and}{\mu }_h$, the aquatic black fly maturity rate, the transmission probabilities from host to vector and vice versa (${\beta }_h\mathrm{and}{\beta }_v$), the aquatic vector carrying capacity and maturity rate ($\mathit{K}\mathrm{and}\mathit{\psi }$), the black fly egg deposition rate ${\pi }_v$ and the rate of transmission of infections from treated hosts r are directly proportional to $R_0$.

However, the human recruitment rate ${\pi }_h$, the ivermectin treatment rate ($\mathit{\gamma }$), the education campain rate ($\mathit{\theta }$), the efficacity of the educational campaign ($\mathit{\sigma }$), the efficacity of larviciding ($\mathit{\epsilon }$), progression rate of treated humans to educated human class ($\mathit{\phi }$), the rate of the immature vector due to larviciding (${\mu }_{\mathrm{\ell }}$), the immature and adult vector removal rates (${\mu }_a\mathrm{and}{\mu }_v$) and the black fly trapping rate (${\mu }_t$) are inversely proportional to ($R_0$).

Our numerical simulation results indicated that importation of river blindness disease by humans is a major contributing factor to the endemicity of the disease in the communities. Furthermore, the simulation results revealed that onchocerciasis can be eradicated if the importation of the disease is properly monitored. Further study can be conducted on the disease using stochastic modelling approach. The challenge of data availability has made it very difficult to incorporate optimal control and cost effectiveness analysis of the model.

Acknowledgments

Authors deeply appreciated the support from colleagues towards the preparation of this manuscript. Much appreciation to other researchers for their numerous review comments and suggestions. Authors have expressed their profound gratitude for such a wonderful support.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

The data used in the analysis of this manuscript is taken from published articles and are cited in this paper. These published articles are also cited at relevant places within the text as references.

Additional information

Funding

The author(s) reported there is no funding associated with the work featured in this article.