Prediction of Energy Concentration during Microwave Heating with a Thermal Diffusion Dimensionless Number

Abstract

In a previous study, the correlation equation with a dimensionless number (As) of local microwave heating was proposed to solve the problem of a wider temperature distribution caused by heat generation within penetration depth during microwave heating. However, the previous model did not account for thermal diffusion. Consequently, a new model, including the Prandtl number, was developed. A boiling experiment for the solution with different Prandtl numbers was carried out during microwave heating, and our old model was developed as an expression that includes the Prandtl number. From the consistent parameter fitting, the developed model will be useful for achieving homogeneous temperature distribution during microwave heating.

Keywords:

• Microwave
• Dimensionless number
• Boiling
• Prandtl number

1. Introduction

In recent years, the microwave heating method has been an alternative to the conventional heating method, and it has been applied for various processes such as drying (Ishibashi et al. 2022), extraction (Mao et al. 2021; Wang et al. 2022), de-emulsification (Martínez-Palou et al. 2013; Santos et al. 2017) and chemical reaction (Macioszczyk et al. 2015; Vinuesa et al. 2022). For example, compared with conventional heating, microwave-assisted reaction shows a faster reaction rate because of the higher heating rate. In the case of an endothermic chemical reaction, heat must be supplied from the heat source by the external device smoothly. When the thermal energy from the wall of the reactor is directly transferred to the reactant or catalyst, the heating rate is relatively slow and inefficient due to the smaller temperature gradient or, the lower thermal conductivity of the reactant. In this conventional scenario, the vessel container is heated up first, and thus the near-wall temperature becomes higher than that of the bulk temperature.

In contrast to conventional heating, microwaves can rotate polar molecules, such as water, and the friction heat is generated directly due to the rearrangement of polar molecular dipoles. Accordingly, the microwave rapidly increases the temperature in the whole volume (Li et al. 2019). On the other hand, microwave energy decays exponentially with depth. In microwave heating, the penetration depth, defined as the depth inside the dielectric medium with 50% of the surface power, is a critical factor. The molecular heating within a vessel is more profound when the microwave penetration depth is comparable to the vessel size. When the vessel size is larger, however, the energy efficiency of microwave heating becomes lower. Moreover, the heat generation within the penetration depth of the microwave causes the temperature nonuniformity, which affects the performance of the reaction yield, the quality of the product and the by-product generation (Bogdal et al. 2006). For example, microwaves can generate localized boiling while the water bulk temperature is lower than 90 °C (Sonobe, Shibata, Asakuma, Hyde, Phan 2020). Therefore, other heat transfer mechanisms are necessary to enhance temperature uniformity when considering the scale-up of microwave equipment. In addition, the inhomogeneity of the electromagnetic field distribution in the sample makes the uniformity of temperature distribution in the vessel more complicated. Therefore, temperature uniformity is one of the critical considerations for the industrialization of the microwave process. For large vessels, the forced thermal convection from the microwave-induced high-temperature region to the low-temperature region becomes more dominant. Although natural convection near the free surface enhances heat transfer to some extent (Zhao et al. 2020), it is not significant enough for temperature uniformity due to the weakness of the convection or the thinner penetration depth of the microwave. For example, when the concentration of electrolyte solution is relatively high, boiling happens quickly from the interface because most of the thermal energy is concentrated in the penetration region (Sonobe, Shibata, Asakuma, Hyde, Nguyen, et al. 2020). Accordingly, forced convection is necessary for temperature uniformity. A detailed heat/mass transfer simulation would require complicated numerical modellings (Yang et al. 2022). In practice, a simple formula to describe heating distribution is more helpful.

In the previous study (Yakata, Sonobe, Asakuma, Hyde, and Phan 2022), a thermal model with two dimensionless numbers, Reynolds number (Re) (Amiraftabi et al. 2020; Munz and Schäfer 2020) and Asakuma number (As) (Sonobe, Shibata, Asakuma, Hyde, Phan 2020; Sonobe, Shibata, Asakuma, Hyde, Nguyen, et al. 2020), has been proposed to predict the temperature distribution during microwave heating. In this case, Re accounts for the fluid mixing effect, while As accounts for the microwave heating within the penetration depth. In this modelling framework, two thermal heating quantities were measured experimentally (Yakata, Sonobe, Asakuma, Hyde, and Phan 2022). First, assuming that energy is absorbed only within the penetration and the energy, q₁ [J] is calculated as follows: (1) $$q_1=V_p\rho C_p\Delta T$$(1) where V_p is the volume of the cylindrical shell of solution in the vessel with a thickness of d_p, ρ and C_p are the density [kg/m³] and specific heat [J/(kg K)] of the solution, and ΔT is the temperature difference between the boiling temperature and the initial temperature. A larger q₁ means wider temperature distribution because the temperature of the solution near the vessel wall or free surface becomes very high.

Secondly, assuming the energy spreads widely in the solution, q₂ [J], is calculated as follows, (2) $$q_2=V_t\rho C_{p}r{t}_b$$(2)

V_t and r are liquid volumes and the rate of change of temperature, respectively. The rate of temperature change is determined from the gradient of temperature versus time graph.

The ratio q₂/q₁ represents the homogeneity of temperature distribution during microwave irradiation. The higher ratio means that thermal energy concentration is strongly generated within the penetration depth by microwave absorption. In the case of boiling experiment without mixing, our dimensionless number, As is sufficient to estimate the thermal energy concentration. However, if the mixing process is added to the microwave heating process, an indicator of mixing must be included in the evaluation formula. The ratio is influenced by stirring mixing conditions, degree of thermal energy concentration and thermal diffusivity. Accordingly, a correlation is used as proposed in a previous study (Yakata, Sonobe, Asakuma, Hyde, and Phan 2022): (3) $$q_2/q_1-1=a\frac{{\mathit{\text{As}}}^c}{{\mathit{\text{Re}}}^b}$$(3)

In the above equation, there are two dimensionless numbers, mixing Reynolds number (Re) and Asakuma number (As) (Sonobe, Shibata, Asakuma, Hyde, Nguyen, et al. 2020). (4) $$\mathit{\text{Re}}=d_s\left(\pi d_s{n}_s\right)/\nu$$(4) (5) $$\mathit{\text{As}}=W/\left(H{d}_p\alpha \rho \right)$$(5)

In Eq.(4)(4) $$\mathit{\text{Re}}=d_s\left(\pi d_s{n}_s\right)/\nu$$(4) , n_s [1/s] is rotational speed, d_s [m] is the length of the magnetic stirrer and ν is the kinetic viscosity of a liquid [m²/s]. It is expected that mixing Reynolds number is inversely related to energy concentration. In Eq.(5)(5) $$\mathit{\text{As}}=W/\left(H{d}_p\alpha \rho \right)$$(5) , W, H, α, and ρ are microwave power [J/s], latent heat of vaporization [J/kg], thermal diffusivity [m²/s] and density of a liquid [kg/m³]. d_p is the penetration depth which can be varied by changing the electrolyte concentration of the solution (Meissner and Wentz 2004). In this case, penetration depth at room temperature was considered when the solution was heated from room temperature. When the initial temperature of the solution is changed, a different penetration depth is used. However, the linear relation was obtained as well. If the temperature dependency of penetration depth varies more significantly, the fitting parameters must be adjusted at lower and higher temperatures.

Finally, the ratio $q_2/q_1$ indicates the uniformity of temperature distribution within a vessel during microwave irradiation. A higher ratio means more localized heating. On the other hand, a lower ratio indicates more homogeneous heating. A similar equation was proposed at a subcooled pool boiling in water at atmospheric pressure (Ivey and Morris 2019). In the case of water or NaCl aqueous solution, parameters became a = 0.065, b = 0.15, c = 1.0. Accordingly, parameter c, the power of As number, is positive for uniformity of temperature distribution. Because As includes microwave power in the numerator and penetration depth of the microwave in the denominator (Sonobe, Shibata, Asakuma, Hyde, Nguyen, et al. 2020; Sonobe, Shibata, Asakuma, Hyde, Phan 2020), the higher number by a higher power and thinner depth causes quick heating at the interface. On the other hand, parameter b, the power of Re, is negative because homogeneous temperature distribution is obtained by a higher mixing rate. Finally, the index of microwave-generated heat and mixing Reynolds number have opposite influences on the thermal energy concentration at the interface. Parameters b and c account for the relative competition between heating and mixing. In this system, the microwave-generated heat is slightly stronger than mixing.

Notably, the existing model, Eq.(3)(3) $$q_2/q_1-1=a\frac{{\mathit{\text{As}}}^c}{{\mathit{\text{Re}}}^b}$$(3) , did not account for thermal convection directly. Furthermore, the heating and mixing effects are separate in Eq. (3)(3) $$q_2/q_1-1=a\frac{{\mathit{\text{As}}}^c}{{\mathit{\text{Re}}}^b}$$(3) , as in numerator and denominator. The interactive effect might be more substantial if the viscosity is relatively higher. In many cases of heat transfer with fluid flow, correlations often use Nusselt number, Nu, or Prandtl number, Pr (Dittus and Boelter 1985). Prandtle number is defined as a dimensionless ratio between momentum diffusivity (kinetic viscosity) to thermal diffusivity: (6) $$\mathit{\text{Pr}}=\nu /\alpha$$(6)

By including Pr in the equation, the correlation formula can be used to balance momentum transport and thermal transport capacity. Consequently, Pr provides a couped effect between heat and mass transfer. This study proposes a new formula: (7) $$q_2/q_1-1=\frac{a\prime {\mathit{\text{As}}}^{c^{\prime }}{\mathit{\text{Pr}}}^{d^{\prime }}}{{\mathit{\text{Re}}}^{b^{\prime }}}$$(7)

In this study, liquids with different thermal properties were used to validate the formulae. In particular, the ethylene glycol/water mixtures were employed to change viscosity and diffusivity. Consequently, these parameters of Eq. (7)(7) $$q_2/q_1-1=\frac{a\prime {\mathit{\text{As}}}^{c^{\prime }}{\mathit{\text{Pr}}}^{d^{\prime }}}{{\mathit{\text{Re}}}^{b^{\prime }}}$$(7) were obtained by heating solutions of different Pr numbers.

2. Experimental

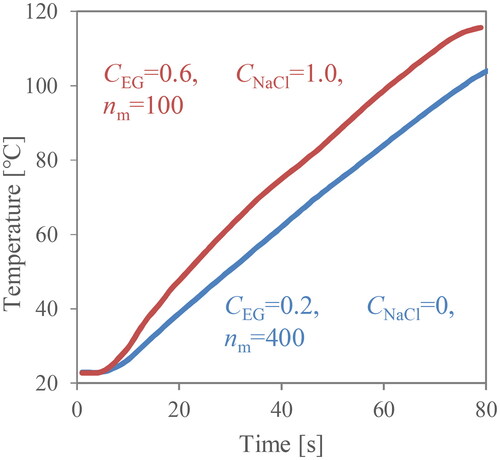
A boiling experiment by microwave heating was carried out for different mixing conditions. A cylindrical vessel of borosilicate glass (diameter of 35 mm and height of 62 mm) is positioned at the centre of the microwave reactor, and a fixed volume (30 mL) of the aqueous solution is heated up (Yakata, Sonobe, Asakuma, Hyde, and Phan 2022). Borosilicate glass is optically transparent with a low dielectric loss factor. So, heat generation on the wall can be neglected. To change solution characteristics, ethylene glycol and sodium chloride were added to distilled water. A cylindrical stirrer was placed at the bottom of the vessel, and rotational velocities were changed for mixing. Experimental conditions are listed in Table 1. The three factors, rotational velocity, sodium chloride and ethylene glycol concentrations, are changed in all combinations. In this experiment, microwave power and the length of the stirrer were fixed at 200 W and 0.024 m. Because there are small holes at the side of the microwave reactor to observe boiling behaviour during the irradiation (Sonobe, Shibata, Asakuma, Hyde, Nguyen, et al. 2020), the time until boiling, t_b [s] was recorded from the movie. The judgment of boiling is visually clear under all conditions, as shown in Figure 1. Moreover, the heating rate at the centre of the vessel, r [K/s] was monitored by the optical fibre. In the experiments, the rates are almost linear due to insignificant heat loss to the wall. Figure 2 is an example of temperature profiles for lower and higher heating rates in this experiment. Although the temperature rise at the centre is delayed more than that near the container wall, an almost linear relation was obtained. The tendency of temperature rise between the liquid in the centre and the near-wall region is the same. However, heat release from the wall can be significant for a long irradiation period. In such cases, a linear relation cannot be obtained.

Figure 1. Images of the interface during the experiments.

Figure 2. Temperature profiles during microwave hearing.

Table 1. Operating conditions.

Rotational velocity, nm [rpm]	100, 200, 300, 400
Sodium chloride concentration, CNaCl [mol/l]	0, 0.05, 0.1, 0.2, 0.5, 1
Ethylene glycol concentration, CEG [vol.%]	0,0.2,0.4,0.6

It should be noted that the vessel size, volume and shape of the fluid body are the same for all experiments. Hence, the physio-chemical properties of aqueous solution are the only variations in this study.

It should be noted that three dimensionless numbers, Re, As, and Pr varied between 639–2555, 65–541 and 6.9–78.4, respectively. The total number of experiments was 96.

3. Results and Discussion

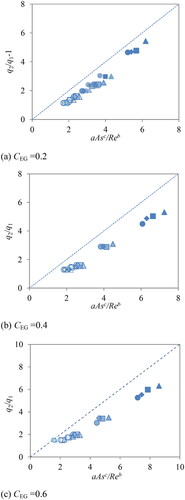
To justify the importance of Pr and Eq. (7)(7) $$q_2/q_1-1=\frac{a\prime {\mathit{\text{As}}}^{c^{\prime }}{\mathit{\text{Pr}}}^{d^{\prime }}}{{\mathit{\text{Re}}}^{b^{\prime }}}$$(7) , Eq. (3)(3) $$q_2/q_1-1=a\frac{{\mathit{\text{As}}}^c}{{\mathit{\text{Re}}}^b}$$(3) was applied to the data with three parameters (Yakata, Sonobe, Asakuma, Hyde, and Phan 2022), as shown in Figure 3. Shapes and the color strength of marks indicate steering speed, n_m (△:100 rpm, □:200 rpm, ◇:300 rpm, ○:400 rpm) and NaCl concentrations, C_NaCl (empty:0, pale:0.05, medium: 0.1-0.2 dark: 0.5, solid:1.0 mol/L). As can be seen in Figure 3, Eq. (3)(3) $$q_2/q_1-1=a\frac{{\mathit{\text{As}}}^c}{{\mathit{\text{Re}}}^b}$$(3) cannot fit the data of water-EG mixtures. Consequently, Eq. (7)(7) $$q_2/q_1-1=\frac{a\prime {\mathit{\text{As}}}^{c^{\prime }}{\mathit{\text{Pr}}}^{d^{\prime }}}{{\mathit{\text{Re}}}^{b^{\prime }}}$$(7) was applied to the data.

Figure 3. Fitting of experimental data and correlation of Eq. (3)(3) $$q_2/q_1-1=a\frac{{\mathit{\text{As}}}^c}{{\mathit{\text{Re}}}^b}$$(3) , a = 0.065, b = 0.15 and c = 0.85.

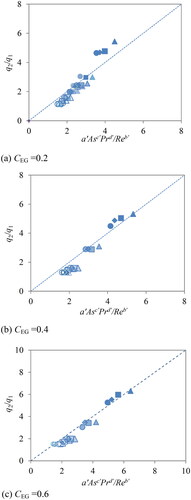
The best-fitted values of the parameters in Eq.(7)(7) $$q_2/q_1-1=\frac{a\prime {\mathit{\text{As}}}^{c^{\prime }}{\mathit{\text{Pr}}}^{d^{\prime }}}{{\mathit{\text{Re}}}^{b^{\prime }}}$$(7) are obtained by fitting the equation against the experimental data. Figure 4 shows fitting plots at different ethylene glycol concentrations, C_EG = 0.2, 0.4 and 0.6. Shapes and the color strength of marks are the same as in Figure 3.

Figure 4. Fitting of experimental data and correlation of Eq. (7)(7) $$q_2/q_1-1=\frac{a\prime {\mathit{\text{As}}}^{c^{\prime }}{\mathit{\text{Pr}}}^{d^{\prime }}}{{\mathit{\text{Re}}}^{b^{\prime }}}$$(7) , a’ = 0.10, b’ = 0.23, c’= 0.77 and d’ = 0.08.

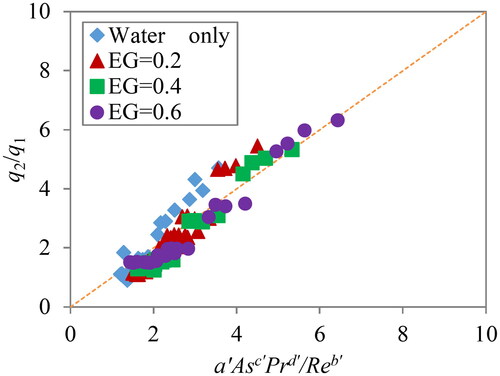
As seen in Figure 4, the linear relations were obtained for all ethylene glycol conditions. In addition to the 96 measurements in this study, the water data from the previous report (Yakata, Sonobe, Asakuma, Hyde, Phan, and Kanti Sen 2022) is also included in Figure 5. It can be seen that the equation fits all data very well. In the case of local heating with a large As, only the surface is rapidly heated before thermal diffusion, and the thermal energy of the absorbance microwave is concentrated on the interface. To achieve homogeneous temperature distribution, stirring by a higher Re number is required. From the absolute values of the parameters, it was found that the As number has the most significant effect on temperature distribution among the three dimensionless numbers. Accordingly, it was confirmed that the correlation equation includes the Pr number, and the equation can be applied to various types of liquid with different kinetic viscosity and thermal diffusivity. However, the effect of Pr on temperature distribution was not so strong because d’ is smaller than c’. As a result, the new model revealed how each dimensionless number influences the temperature distribution. Finally, the model can contribute to the stirring conditions to obtain uniform temperature distribution during microwave heating.

Figure 5. Fitting of experimental data and correlation of Eq. (7)(7) $$q_2/q_1-1=\frac{a\prime {\mathit{\text{As}}}^{c^{\prime }}{\mathit{\text{Pr}}}^{d^{\prime }}}{{\mathit{\text{Re}}}^{b^{\prime }}}$$(7) . The data for water was obtained from the previous report (Yakata, Sonobe, Asakuma, Hyde, and Phan 2022).

4. Conclusions

In this study, boiling experiments were conducted to obtain homogeneous temperature distribution during microwave heating by changing the Prandtl of the solution. The formula provides a combination of (i) microwave heating within the penetration layer, (2) fluid mixing in bulk and (3) momentum/thermal transport throughout the fluid. It was found that including Pr provides a consistent prediction for different water-EG mixtures. The developed model is useful for controlling homogeneity when a different type of solution with different physical properties is heated up by microwave in industrial processes.

Nomenclature
a	=	Parameter in Eq. (3)(3) $$q_2/q_1-1=a\frac{{\mathit{\text{As}}}^c}{{\mathit{\text{Re}}}^b}$$(3)
a'	=	Parameter in Eq. (7)(7) $$q_2/q_1-1=\frac{a\prime {\mathit{\text{As}}}^{c^{\prime }}{\mathit{\text{Pr}}}^{d^{\prime }}}{{\mathit{\text{Re}}}^{b^{\prime }}}$$(7)
As	=	Dimensionless number of microwave local heating [-]
b	=	Parameter in Eq. (3)(3) $$q_2/q_1-1=a\frac{{\mathit{\text{As}}}^c}{{\mathit{\text{Re}}}^b}$$(3)
b'	=	Parameter in Eq. (7)(7) $$q_2/q_1-1=\frac{a\prime {\mathit{\text{As}}}^{c^{\prime }}{\mathit{\text{Pr}}}^{d^{\prime }}}{{\mathit{\text{Re}}}^{b^{\prime }}}$$(7)
c	=	Parameter in Eq. (3)(3) $$q_2/q_1-1=a\frac{{\mathit{\text{As}}}^c}{{\mathit{\text{Re}}}^b}$$(3)
c'	=	Parameter in Eq. (7)(7) $$q_2/q_1-1=\frac{a\prime {\mathit{\text{As}}}^{c^{\prime }}{\mathit{\text{Pr}}}^{d^{\prime }}}{{\mathit{\text{Re}}}^{b^{\prime }}}$$(7)
C EG	=	Ethylene glycol concentration [vol.%]
C NaCl	=	NaCl concentration [mol/l]
Cp	=	Specific heat [J/ (kg K)]
d '	=	Parameter in Eq. (7)(7) $$q_2/q_1-1=\frac{a\prime {\mathit{\text{As}}}^{c^{\prime }}{\mathit{\text{Pr}}}^{d^{\prime }}}{{\mathit{\text{Re}}}^{b^{\prime }}}$$(7)
dp	=	The penetration depth of the solution [m]
ds	=	Length of stirrer [m]
H	=	Latent heat of vaporization [J/kg]
nm	=	Rotational speed [rpm]
ns	=	Rotational speed [1/s]
Nu	=	Nusselt number [-]
Pr	=	Prandtl number [-]
q1	=	Energy when the microwave is absorbed within the penetration depth [J]
q2	=	Energy when the microwave is absorbed in the whole vessel [J]
r	=	Heating rate [K/s]
Re	=	Mixing Reynolds number [-]
tb	=	Boiling time [s]
Vp	=	The volume of water within the penetration depth (from the free surface) [m3]
Vt	=	Volume of solution [m3]
W	=	Microwave power [J/s]
α	=	Thermal diffusivity of solution [m2/s]
ΔΤ	=	The temperature difference between boiling temperature and the initial temperature [K]
ν	=	Kinetic viscosity of the solution [m2/s]
ρ	=	Density of solution [kg/m3]

Disclosure Statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This study was conducted with support from Tanigawa Thermal Technology Promotion Fund.