Mechanisms preventing animals to achieve buoyant flight

ABSTRACT

In the 300-million-year evolutionary history of animal flight, fliers have universally evolved to exploit the physical principle of drag, whereby an animal uses wings to achieve lift. However, the treehopper Oeda – an Amazonian insect exhibiting a grotesquely large balloon-like thorax – has been described in what may be the only account of an animal engaging in buoyant flight, whereby an animal fills body cavities with low-density air to float, akin to a hot-air balloon. We use Oeda as a study system to conduct a theoretical analysis exploring the biomechanics of buoyant flight and the mechanisms preventing its widespread occurrence in animals. We show that not even an organism with the unique and disproportionate dimensions of Oeda can buoy more than 1% of its body weight. Instead, our results suggest Oeda’s bloated thorax is a hindrance for flight that has selected for larger wings to compensate for the species’ disproportionate dimensions. Our analysis illustrates that animals may only achieve buoyant flight by filling cavities thousands of times larger than the body with heated low-density biogases. Still, the evolution of such traits is likely restricted by a variety of developmental and ecological factors that have prevented animals from evolving buoyant flight. Whether any animal has evolved the means to conquer buoyant flight remains to be found in nature.

KEYWORDS:

• Flying
• insect
• lift
• locomotion
• Membracidae
• Oeda

Introduction

Animal flight evolved in insects more than 300 million years ago, and it subsequently evolved at least three more times independently, in birds, pterosaurs and bats (Lighthill 1975; Misof et al. 2014). Fliers have universally evolved to exploit the physical mechanism of drag, whereby they rely on wings to push air down and lift the body (Dickinson 2006; Gleiss et al. 2011). Another potential mechanism, however, is that of buoyancy, whereby fliers would fill body cavities with low-density gases, reducing the density of their bodies in relation to air, and float akin to a hot air balloon. Buoyancy is ubiquitous in aquatic animals and has the potential to be a more energetically efficient means of vertical locomotion than the energetically demanding winged flight (McNeill 1990; Gleiss et al. 2011). Buoyancy’s energetic efficiency even served as a basis for Carl Sagan to theorise ‘Jovian floaters’ inhabiting Jupiter’s upper atmosphere (Sagan and Salpeter 1976; McNeill 1990; Cerceau 2010). However, despite its physical plausibility and potential ecological benefits, buoyant flight has not been demonstrated in any animal species yet.

The Archimedes principle (B = V × (ρ_e – ρ_b)) predicts that buoyant flight will be achieved if an animal generates enough buoyant force (B) to overcome its weight (w ≤ B). Animals could do so by filling sufficiently large body cavities (V) with low-density gases and/or by heating the air inside the cavity (ρ_b). Animals may also take advantage of conditions of high air density, such as at low elevations (ρ_e). The magnitude of the buoyant force relative to the body weight would determine how fast an animal ascends (w < B) or sinks (w > B).

One observation proposes that the treehopper Oeda (Hemiptera, Membracidae) exploits the principle of buoyancy to fly (Richter 1954). Treehoppers are insects whose thorax has evolved into incredibly diverse forms; in the case of Oeda, it has taken the form of a grotesquely large hollow balloon covering the body (Figure 1). The following English translation of Richter’s original observations describes Oeda’s buoyant process as follows:

It [ie the thorax] is much larger than the body, being its length (once extrapolated) 14 to 15 times larger. This fact allows the species hamulata to employ the appendix as a hot air balloon. While feeding the insect always sits over a sunny leaf. Temperature measured under the sun in the jungle – that is, surrounded by shadows, is 6 to 10 degrees [Celsius] higher than the temperature measured in the shade. By slightly lifting the appendix [ie the thorax] by lowering the abdomen, the insect is able to use the fine membrane as a valve. These movements are easily noticeable in insects sitting in the sun. When startled, it lifts and moves quickly upward towards shelter in the treetops. There, it lets the air trapped in the appendix cool little by little, descending branch after branch; it returns to the host plant, again to a sunny spot.

For whole weeks I observed this procedure daily. Males are known for the increased speed of their ‘hot air balloon flights’ compared to the heavier females.

[…] The smaller species of the same genus like p. e. inflata (other species are not known for Colombia) do not employ the appendix as described above. Apparently, the smaller appendix is not able to carry the insect’s body …. (Richter 1954, p. 365−367; for the original text in Spanish see Appendix A1)

Figure 1. Oeda species and their distribution over the Amazon. Note the overall high air density across the species distribution.

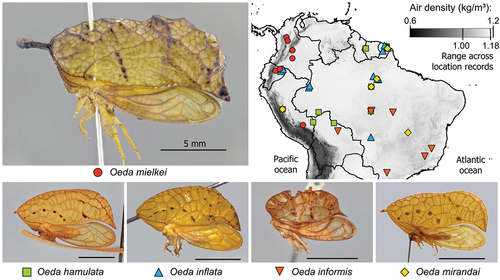
While Richter’s comments focus on O. hamulata, illustrations of the subject of his observations (ie fig. 62, p. 366) demonstrate he is likely referring to O. mielkei, which was described 70 years later (Sakakibara 2014).

Oeda may greatly benefit from an energetically efficient way of vertical locomotion in their Amazonian habitat, where high air density and the complex vertical structure of the forest should create a suitable niche for buoyant flight (Figure 1). Inspired by Richter’s observations and the extraordinary proportions of Oeda, we studied the physical basis of buoyant flight and the mechanisms preventing its widespread occurrence in animals. We perform a theoretical assessment of the morphological and physical conditions that would allow an animal to achieve buoyant flight, and the degree to which Oeda species meet these criteria. We also looked for morphological evidence of any ecological benefit species might derive from buoyancy.

Materials and methods

We estimated Oeda’s buoyancy in its habitat based on information from museum specimens of all five species (Figure 1). For each specimen, we assessed morphology from lateral and dorsal photographs, and environmental conditions from location records based on data from WorldClim (Fick and Hijmans 2017).

We estimated thorax volumes (V) by approximating its shape to an ellipsoid and calculating the volume using the thorax’s width, length, and height (Appendix A2, Equation A1, Figure A1). We also calculated the thorax lateral plane area and the overall surface (Appendix A2, Equations A2, A3), which are relevant for calculations on thorax air density below. Oeda’s thorax is a rigid structure and should not change in dimensions with changes in internal pressure. Environment air density (ρ_e) calculations were made using the mean annual temperature and atmospheric pressure derived from elevation (Appendix A2, Equations A4, A5). Thorax air densities (ρ_b) were calculated using temperatures calculated from an energy balance model that considers heat input from solar and environment-reflected radiation onto the thorax, and heat loss from the thorax towards the air (Appendix A2, Equation A6). Finally, we used the Archimedes equation (B = V × (ρ_e – ρ_b)) to estimate each specimen’s buoyancy as the percentage of body weight lifted. Specimen body weight was obtained by averaging estimates from two empirical equations inferring insect wet body weight from insect body length (Sage 1982; Straus and Avilés 2017) (Figure A1).

We assessed the physical conditions necessary for animal buoyant flight by calculating buoyancy generated across a matrix with a theoretical range of buoyant-cavity volumes relative to body mass and a range of densities inside buoyant cavities relative to the environment, between 0% and 100%. Along this matrix, we mapped Oeda’s buoyancy. We also mapped the buoyancy that would be generated by buoyant cavities theoretically filled with air, methane, or hydrogen (ie low-density biogases) heated 15°C above the environment, which approximates the physiological thermal limit of animals (Hoffman et al. 2013). These calculations were performed with the following reference conditions: environmental temperature of 15°C and air density of 1.225 kg/m³ (ie at sea level).

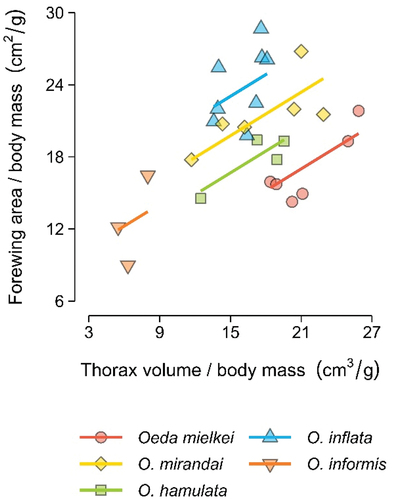
Finally, we looked for signs of ecological benefits that Oeda might derive from buoyancy using a generalised linear mixed model (GLMM) testing for shifts in specimens’ forewing area as a function of thorax volume. A negative correlation between thorax volume and wing area may signal a selective process of buoyant flight in favour of drag flight. Forewing area was calculated by approximating its shape to a rhombus and calculating its area using the lengths of the structure’s diagonals (Appendix A2, Equation A7, Figure A1). We implemented thorax volume and forewing areas as ratios to body mass to control for the effects of body size. GLMM used species as random effects (n = 5) and specimens as units of analysis (n = 27), where sample size per species was: four O. hamulata, eight O. inflata, three O. informis, six O. mielkei, and six O. mirandai.

Analyses were carried out in R v. 3.2.2 (R Core Team 2020). We used the packages dplyr for data management (Wickham et al. 2021); glmmTMB (Brooks et al. 2017) for GLMM construction; car (Fox and Weisberg 2019) for p value calculations; and ggplot2 (Wickham 2016), ggpubr (Kassambara 2020), ggnewscale (Campitelli 2022) and lemon (McKinnon 2020) for figure design. Geographical analyses were carried out in QGIS (QGIS.org 2022). The data and analytical code that support the findings of this study are openly available in Mendeley Data at https://data.mendeley.com/, reference number doi:10.17632/wk66mk9z94.1 (Camacho 2024).

Results

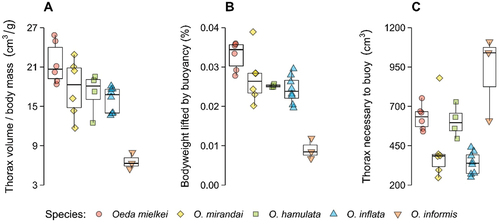
We found that animals may buoy their body weight with buoyant-cavity volumes of at least 10,000 cm³ per g of body mass if relying on heated air, and 1000 cm³ per g if relying on heated low-density biogases (Figure 2). In their environment, Oeda species may heat air inside the thorax by 3.96 ± 0.14°C and reduce density by 1.3 ± 0.048% (Figure 2). Weighing 0.0086 ± 0.0013 g and with thoraxes measuring 0.13 ± 0.24 cm³ (Figure 3A), Oeda species are only able to buoy 0.02 ± 0.004% of their body weight in their habitat (Figure 3B). Under these conditions, species could only overcome gravity if their thoraxes had outrageous proportions of 585.12 ± 99.58 cm³ (Figure 3C).

Figure 2. Animal buoyancy across theoretical conditions of body cavity size and density differential relative to the environment. Coloured symbols and lines represent median values of Oeda species with thoraxes filled with sun-heated air. Dotted lines depict density differentials with cavities filled with air, methane, and hydrogen at a presumed physiological thermal limit of 15°C above the environment (Hoffman et al. 2013). The y-axis points at which dotted lines intersect with the limit of the black area represent the buoyant cavity volumes necessary to overcome the body weight. Calculations based on reference conditions of environment temperature of 15°C and air density of 1.225 kg/m³.

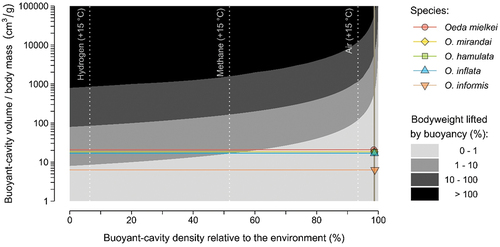
Figure 3. Oeda species’ (A) thorax volume relative to body mass; (B) buoyancy capability in their environment with the sun heating air inside the thorax; and (C) thorax volume necessary for buoyancy to overcome body weight.

After correcting for body weight, Oeda species thorax volume was found to be positively correlated with wing area (GLMM: slope (cm²/g) = 0.060 ± 0.014, χ² = 17.62, p < .01) (Figure 4).

Figure 4. Oeda’s wing surface as a function of thorax volume. Points represent specimens and lines represent the best fit of a generalised linear mixed model using species as random effects. Thorax volume and forewing area are presented as ratios to body mass, to control for body size.

Discussion

The extreme morphological and physical conditions required by an animal to become buoyant in air illustrate the challenges preventing buoyant flight from being widespread in the animal kingdom. Even for an animal with the extraordinary proportions of Oeda, buoyancy capabilities are negligible. This demonstrates that Oeda cannot buoy towards treetops using the heat of the sun, never mind descend gradually after cooling as reported by Richter (1954). In fact, our results suggest Oeda’s bloated thorax is a hindrance for flight that has selected for larger wings to compensate for species’ disproportionate dimensions.

The question remains: What is the adaptive value of Oeda’s thorax? One possibility is predator avoidance, where the thorax acts as a masquerade of a dead leaf or an empty butterfly pupa, or as a decoy that draws a predator attack, leaving the insect’s body unharmed and able to flee (Cryan and Deitz 1999). Another possibility is thermoregulation (Cryan and Deitz 1999). The balloon-shaped thorax maximises volume while minimising surface area, thus reducing heat convection. Being an empty structure reduces heat conduction. Light colours reduce heat gain by sun radiation. Thus, Oeda’s thorax may work as a heat shield protecting the body from the sun, which may allow the insect to feed on top of leaves exposed to the sun as described by Richter.

For buoyant flight to be possible, a key biomechanical solution for any organism is to evolve body cavities thousands of times larger than their bodies. Yet the evolution of such disproportionate dimensions is likely restricted by a variety of developmental and ecological factors. Effective buoyant cavities need to be large, light, and structurally stable under the stress of the environment and predators. Such cavities may not be ecologically viable due to increased developmental times, limited mobility, and increased predation risk (Lima and Dill 1990; Gillooly et al. 2002). For instance, developmental challenges aside, the ecological viability of a 5 mm Oeda manoeuvring a 1000 cm³ thorax (Figure 3C) across dense vegetation and while being exposed to high predation rates in the Amazon is absurd (Roslin et al. 2017; Camacho and Avilés 2019). Sagan reached similar conclusions in theorising Jupiter’s Jovian ecosystem, where kilometre-sized floaters are viable only in the vast calm regions of the upper atmosphere (Sagan and Salpeter 1976; Cerceau 2010).

Relying on heat to reduce density inside buoyant cavities presents additional ecological and energetic challenges. Relying on sun energy may be energetically inexpensive but is also problematic. Small organisms, such as Oeda, may lack the surface to capture enough energy, whereas large organisms may take too long to warm (Sagan and Salpeter 1976). Moreover, sun energy depends on the time of day, cloud cover and season, which would limit the spatiotemporal niche of buoyant flight. Thermoregulatory animals, such as endothermic vertebrates and many winged insects, could solve these issues by relying on active metabolism to heat air inside buoyant cavities (Heinrich 1995). However, this may be energetically unviable.

Relying on temperature alone to reduce density inside buoyant cavities achieves limited buoyancy unless coupled with low-density gases. Still, relying on low-density gases presents evolutionary challenges of its own. Animals may only have access to the few biogases that are lighter than air (eg ammonia, methane, and hydrogen) by evolving associations with microbial symbionts (Sugimoto et al. 1998; Dhodari and Spiteller 2021). Additionally, animals would need to evolve mechanisms to quickly metabolise such gases to be able to manoeuvre. Our analyses show that methane-filled cavities may generate nearly as much buoyancy as hydrogen (ie the lightest gas). The generation of methane in the gut is common across the animal kingdom, and, thus, a modified gut may be the most parsimonious mechanism for the evolution of animal buoyant flight.

The low density of air thus remains an insurmountable challenge for the evolution of buoyant flight. In contrast, a high-density medium such as water (approximately 800 times denser than air) has allowed most aquatic organisms to evolve mechanisms to buoy while swimming (McNeill 1990). However, high air density during the early Cenozoic (ie 1.56 kg/m³, 29% higher than today) facilitated the evolution of flight in winged fliers and could have also facilitated the evolution of buoyant flight during the early evolution of Oeda (Dudley 2000; Wang et al. 2020). In fact, recalculating buoyancy under such air density conditions shows that proto-Oeda may have overcome gravity with a (perhaps more ecologically viable) thorax of 19.5 ± 2.9 cm³ while being heated by the sun.

We show that creating enough buoyancy to derive any ecological benefit is implausible even for an organism with such unique and disproportionate dimensions as Oeda. Under current environmental conditions, the traits necessary to overcome the biophysical challenge of low air density may be ecologically and evolutionary unviable. Whether any animal has evolved the means to conquer buoyant flight remains to be found in nature.

Acknowledgements

We thank the invertebrate museum at the Universidad Católica del Ecuador (QCAZ, Quito, Ecuador), the biological collection at the Universidad de Medellín CES (CEBUCES, Medellín, Colombia), the entomological collection at the Universidad de Antioquia (CEUA, Medellín, Colombia), the zoological collection at the Universidade de São Paulo (MZUSP, São Paulo, Brazil), and the Smithsonian National Museum of Natural History (USNM, Washington DC, USA). Special thanks to Alejandro Camacho and Stuart McKamey for their support. This study was self-funded.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Supplementary data

Supplemental data for this article can be accessed online at https://doi.org/10.1080/00222933.2024.2322178.

Additional information

Funding

The author(s) reported there is no funding associated with the work featured in this article.