Ramsey interferometry with cold atoms in coherent population trapping

ABSTRACT

The utilization of Ramsey interferometry via coherent population trapping (CPT), which enables the optical interrogation of microwave transitions without the reliance on microwave cavities, plays a crucial role in the advancement of compact and low-power quantum sensors. Particularly, high-resolution CPT-Ramsey spectroscopy of alkali-metal atoms has found extensive application in constructing miniaturized quantum sensors like atomic magnetometers and atomic clocks. Due to their well-defined environment and extended coherence time, cold atoms offer enhanced sensitivity and precision in CPT-Ramsey interferometry. This review comprehensively examines CPT-Ramsey interferometry with cold atoms, encompassing both conventional and multi-pulse techniques, and explores their potential applications in practical quantum sensors.

KEYWORDS:

• Coherent population trapping
• Ramsey interferometry
• cold atoms
• quantum sensors

1. Introduction

Coherent population trapping (CPT) arises from quantum interference among different transition paths, initially discovered in a three-level Λ system coupled with two quasi-resonant laser fields [1,2]. These laser fields coherently excite atoms from two ground states to a common excited state. When the frequency difference between the two laser fields matches the separation of the two ground states, a coherent superposition of the ground states emerges, leading to a dark state where atoms cease to absorb laser fields. This unique superposition state is termed a dark state, resulting in no atoms being excited to the higher state and causing a narrow ‘black’ (or ‘bright’) line to appear in the fluorescence (transmission) spectrum. Since the initial observation of CPT in sodium vapor [3], it has been identified in diverse physical systems ranging from alkali-metal atoms [4] to single nuclear spins in diamond defects [5] and artificial atoms [6,7]. Leveraging the all-optical manipulation of quantum states, CPT has found extensive applications in quantum engineering and quantum metrology, including atom cooling [8], atomic clocks [9–18], and atomic magnetometers [19–24].

Ramsey interferometry, employing separated oscillatory fields to manipulate atoms, stands as a potent tool with diverse applications in both fundamental research and practical technology [25,26]. In its operation, the first pulse initially excites atoms into a superposition of two internal states, denoted as $|\mathit{a}⟩$ and $|\mathit{b}⟩$. Following this, the atoms undergo free evolution within a coherent superposition, characterized by a time-dependent relative phase, until the second pulse is applied. If the second pulse is in phase with the oscillating superposition, atoms complete the transition to state $|\mathit{b}⟩$; conversely, when the second pulse is half a cycle out of phase, the atoms revert to the state $|\mathit{a}⟩$. Ultimately, the interference fringe pattern is observed by detecting the atomic population, providing a basis for high-precision spectroscopy. However, it is noteworthy that the probing electromagnetic field’s perturbation on the atomic transition can induce frequency shifts [27]. To address this issue, sophisticated interrogation schemes like auto-balanced Ramsey spectroscopy [28–30] and hyper-Ramsey spectroscopy [31–33] have been developed to achieve high resolution and mitigate laser-induced frequency shifts.

To distinguish it from conventional Ramsey interferometry utilizing a two-level system, the version employing coherent population trapping (CPT) is termed CPT-Ramsey interferometry, also known as Raman-Ramsey interferometry [34]. Similar to conventional Ramsey interferometry, CPT-Ramsey involves Raman interactions with a long CPT pulse (preparation pulse), followed by a free-evolution period, and subsequently another Raman interaction with a short CPT pulse (query pulse). Unlike conventional Ramsey interferometry, the CPT pulse is not a typical $\frac{\pi }{2}$-pulse. The preparation pulse is deliberately prolonged to optically pump as many atoms as possible into the dark state via CPT. Conversely, the query pulse is kept short to avoid perturbing the dark state and affecting the detection of the accumulated phase difference between the evolving dark state and the Raman fields’ phase.

Ramsey spectroscopy utilizing CPT demonstrates outstanding resolution with a narrow fringe width, akin to Ramsey interferometry with two-level systems. However, as the free-evolution time increases, discerning the central CPT-Ramsey fringe from adjacent ones becomes challenging, given that the adjacent-fringe amplitudes approach the central-fringe amplitude. To address this issue, multi-pulse CPT-Ramsey interference techniques such as multi-pulse phase-stepping [35], repeated query [36] and the temporal analog of Fabry-Pérot resonator (FPR) [37] are employed. CPT-Ramsey interferometry proves indispensable in precision measurements, particularly high-resolution CPT-Ramsey spectroscopy of alkali-metal atoms, garnering significant interest in the development of miniaturized quantum sensors.

Cold atoms, owing to their clear environment and low temperatures, play crucial roles in both fundamental scientific research and practical technological applications. The CPT-Ramsey interferometry with cold atoms holds promise for enhancing the sensitivity and precision of quantum sensors, given the extended coherence time of cold atoms and the absence of pressure-induced frequency shifts caused by buffer gases. In this review, we delve into the implementation of CPT-Ramsey interferometry with cold atoms, covering conventional CPT-Ramsey interferometry, multi-pulse CPT-Ramsey interferometry, and their potential applications in the realm of quantum sensors. The structure of the remaining review is as follows. The remaining of this review is structured as following. Section II provides an introduction to conventional CPT-Ramsey interferometry, encompassing the theoretical model, two-zone CPT-Ramsey interference of an atomic beam, and two-pulse CPT-Ramsey interference of a free-falling ensemble. Section III explores the utilization of multi-pulse CPT-Ramsey interferometry to enhance sensitivity and accuracy. The potential applications are discussed in Section IV. The concluding section offers a brief summary of the key findings and insights presented in this review.

2. Conventional CPT-Ramsey interferometry

The single-pulse CPT spectroscopy has the drawback of power broadening, which decreases the measurement precision of the atomic transition frequency. The CPT-Ramsey interferometry can overcome this drawback as its linewidth $\mathrm{\Delta \nu }=1/2\mathit{T}$ is independent on the CPT field intensity. The high-resolution CPT-Ramsey spectroscopy of alkali-metal atoms has been widely used in miniaturized quantum sensors. In this section, we focus on the conventional CPT-Ramsey interferometry with cold atoms including two-zone and two-pulse schemes, and give a generally theoretical model for CPT-Ramsey interference.

2.1. Theoretical model for CPT-Ramsey interference

Due to alkali-metal atoms with abundant ground-state hyperfine Zeeman levels, the CPT phenomenon could form several dark states when the frequency difference between the bichromatic fields matches the hyperfine splitting [38]. The $\mathit{\sigma }-\mathit{\sigma }$ configuration employing circularly polarized laser light is commonly utilized in a typical CPT clock. However, the circularly polarized light will pump a significant fraction of atoms into their Zeeman edge states (also called trap states, see Figure 1(a)), which will reduce the contrast of the CPT signal. The double-Λ configurations could automatically prevent the formation of trap states, which include the lin$||$lin polarization scheme and the lin$\perp$lin polarization scheme, identical to the push-pull optical pumping and the orthogonal circular polarization scheme [38–40]. As the M and W systems are formed for the excited states with angular momenta $F_e>1$, the corresponding contrast of the CPT signal in the lin$||$lin configuration do not have enough enhancement than that of $\mathit{\sigma }-\mathit{\sigma }$ configuration. But for atoms with nuclear spin $\mathit{I}=3/2$, high CPT resonance contrast was observed in the lin$||$lin configuration as only Λ systems were formed [38].

Figure 1. Different configurations constructed by the D1 line of ⁸⁷Rb atoms. (a) $\mathit{\sigma }-\mathit{\sigma }$ configuration. (b) Lin$||$ configuration. (c) Lin$\perp$lin configuration.

Below we concentrate on the use of the D1 line of ⁸⁷Rb atoms to compare the difference of these configurations (see Figure 1). In the lin$||$lin configuration, the frequency components of the bichromatic fields have the same linear polarization. Therefore, the ${\sigma }^{+}$ and σ⁻ transitions could be simultaneously excited. However, the dark states arising from ${\sigma }^{+}-{\sigma }^{+}$ and ${\sigma }^{-}-{\sigma }^{-}$ are orthogonal and interfere destructively [41]. So the transition of $|F_g=1,\text{break}{m}_F=0⟩\to |F_g=2,m_F=0⟩$ has no contribution to the CPT signal. The other two separate Λ systems are formed via ${\sigma }^{+}-{\sigma }^{-}$ coupling the ground-state sublevels $|F_g=1,m_F=\pm 1⟩$ and $|F_g=2,m_F=\mp 1⟩$ to the common excited state $|F_e=1,m_F=0⟩$. Under a weak magnetic field, these two Λ systems are nearly identical as the g factors of different ground-state hyperfine levels have an almost equal absolute value and opposite signs. When neglecting the contribution of the nuclear spin to the Zeeman splitting, the two-photon resonance frequencies of $|F_g=1,m_F=+1⟩\to |F_g=2,m_F=-1⟩$ and $|F_g=1,m_F=-1⟩\to |F_g=2,m_F=+1⟩$ transitions are equal to that of $|F_g=1,m_F=0⟩\to |F_g=2,m_F=0⟩$ transition.

The lin$\perp$lin polarization scheme utilizes two linearly orthogonally polarized lights to make up the bichromatic fields. Different from the lin$||$lin configuration, this scheme can form a double-Λ system that interrogate $|F_g=1,\text{break}{m}_F=0⟩\to |F_g=2,m_F=0⟩$ transition (see Figure 1(c)). Due to the phase relation between the Rabi frequencies of each transition of the Λ systems, the particular superposition of the states is dark for both excited states $|F_e=1,m_F=-1⟩$ and $|F_e=1,m_F=+1⟩$ [34]. Like the lin$||$lin configuration, two other Λ systems are also made via the Δm = 2 transitions $(|F_g=1,m_F=\pm 1⟩\to |F_g=2,m_F=\mp 1⟩)$. Equivalent conditions of optical pumping have been demonstrated for the push-pull optical pumping and the orthogonal circular polarization with counter-propagating waves [39,42].

In the double-Λ configuration, although there are several CPT resonances from different transitions of $\mathrm{\Delta }\mathit{m}=2$, the two-photon resonance frequencies of those transitions are almost identical in a weak magnetic field. Hence, single-Λ system is employed to elucidate the CPT-Ramsey interferometry, while the double-Λ system exhibits analogous characteristics [43]. Figure 2 shows a typical Λ system including two ground states ($|1⟩$ and $|2⟩$) and a common excited state ($|3⟩$). Two laser fields with a frequency difference equal to the splitting ω between $|1⟩$ and $|2⟩$ are applied to couple the Λ system. The δ₁ and δ₂ are single-photon detunings from the corresponding optical resonances, respectively. The two-photon detuning Δ and the average detuning δ are defined as $\mathrm{\Delta }={\delta }_1-{\delta }_2$ and $\mathit{\delta }=({\delta }_1+{\delta }_2)/2$, respectively. The Rabi frequencies for the transitions from the two ground states to the common excited state are expressed as Ω₁ and Ω₂, respectively. Γ is the total decay rate of spontaneous emission from the excited state to the ground states, which is composed by Γ₃₁ and Γ₃₂. The decoherence between the ground states is described by the dephasing term of γ_c. The state of the Λ system, which is described by the density matrix ρ_ij ($\mathit{i},\mathit{j}=1,2,3$), obeys the Liouville equation [43,44],

Figure 2. (a) Closed three-level Λ configuration coupled by two laser fields with Rabi frequencies Ω₁ and Ω₂. (b) Timing diagram for the CPT-Ramsey interference.

(1) $\begin{array}{l}\frac{d}{\mathit{dt}}\mathit{\rho }=-\frac{i}{\hslash }[\mathit{H\rho }-\mathit{\rho H}]+\mathcal{R}\mathit{\rho }\end{array}$(1)

where the Hamiltonian H describes the interaction between the atomic system and the laser fields, and the matrix $\mathcal{R}\mathit{\rho }$ takes into account the effects of relaxation and decoherence.

Under the rotating wave approximation (RWA), the Hamiltonian H is given as

(2) $\begin{array}{l}\mathit{H}=\mathit{\hslash }\left(\begin{array}{lll}{\delta }_1& 0& \frac{{\mathrm{\Omega }}_1}{2}\\ 0& {\delta }_2& \frac{{\mathrm{\Omega }}_2}{2}\\ \frac{{\mathrm{\Omega }}_1}{2}& \frac{{\mathrm{\Omega }}_2}{2}& 0\end{array}\right)\end{array}$(2)

Generally, the matrix $\mathcal{R}\mathit{\rho }$ can be given as

(3) $\begin{array}{l}\mathcal{R}{\rho }_{\mathit{ij}}=\left(\begin{array}{lll}{\mathrm{\Gamma }}_{31}{\rho }_{33}& -{\gamma }_c{\rho }_{12}& -{\mathrm{\Gamma }}_{31}{\rho }_{13}\\ -{\gamma }_c{\rho }_{21}& {\mathrm{\Gamma }}_{32}{\rho }_{33}& -{\mathrm{\Gamma }}_{32}{\rho }_{23}\\ -{\mathrm{\Gamma }}_{31}{\rho }_{31}& -{\mathrm{\Gamma }}_{32}{\rho }_{32}& -\mathrm{\Gamma }{\rho }_{33}\end{array}\right)\end{array}$(3)

For alkali-metal atoms, we have ${\mathrm{\Gamma }}_{31}\approx {\mathrm{\Gamma }}_{32}=\mathrm{\Gamma }/2$. From the Liouville equation under the RWA, one can easily obtain the optical Bloch equations for the time-evolution of the density matrix elements,

(4) $\begin{array}{ll}\frac{\mathit{d}{\mathit{\rho }}_{11}}{\mathit{dt}}=& -{\mathrm{\Omega }}_1\text{Im}({\rho }_{13})+{\mathrm{\Gamma }}_{31}{\rho }_{33},\\ \frac{\mathit{d}{\mathit{\rho }}_{22}}{\mathit{dt}}=& -{\mathrm{\Omega }}_2\text{Im}({\rho }_{23})+{\mathrm{\Gamma }}_{32}{\rho }_{33},\\ \frac{\mathit{d}{\mathit{\rho }}_{33}}{\mathit{dt}}=& {\mathrm{\Omega }}_1\text{Im}({\rho }_{13})+{\mathrm{\Omega }}_2\text{Im}({\rho }_{23})-\mathrm{\Gamma }{\rho }_{33},\\ \frac{\mathit{d}{\mathit{\rho }}_{13}}{\mathit{dt}}=& -(\frac{\mathrm{\Gamma }}{2}+\mathit{i}{\delta }_1){\rho }_{13}+\mathit{i}\frac{{\mathrm{\Omega }}_2}{2}{\rho }_{12}-\mathit{i}\frac{{\mathrm{\Omega }}_1}{2}({\rho }_{33}-{\rho }_{11}),\\ \frac{\mathit{d}{\mathit{\rho }}_{23}}{\mathit{dt}}=& -(\frac{\mathrm{\Gamma }}{2}+\mathit{i}{\delta }_2){\rho }_{23}+\mathit{i}\frac{{\mathrm{\Omega }}_2}{2}{\rho }_{21}-\mathit{i}\frac{{\mathrm{\Omega }}_2}{2}({\rho }_{33}-{\rho }_{22}),\\ \frac{\mathit{d}{\mathit{\rho }}_{12}}{\mathit{dt}}=& -({\gamma }_c+\mathit{i}\mathrm{\Delta }){\rho }_{12}+\mathit{i}\frac{{\mathrm{\Omega }}_2}{2}{\rho }_{13}-\mathit{i}\frac{{\mathrm{\Omega }}_1}{2}{\rho }_{32}\end{array}$(4)

with ${\rho }_{\mathit{ji}}={\rho }_{ij}^{\ast }$. The population conservation of the closed system is given by ${\rho }_{11}+{\rho }_{22}+{\rho }_{33}=1$.

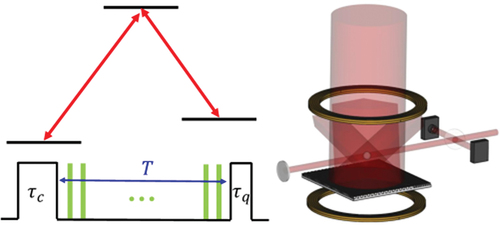
Like conventional Ramsey interferometry, pulsed CPT excitation in the three-level Λ system creates Ramsey interference pattern. In this case, the first pulse should be long enough to allow the atoms to prepare into the dark state, while the second pulse should be short enough to avoid repumping the atoms into the dark state again. As the timing diagram in Figure 2(b), the length of the long pulse (preparation pulse) should satisfy ${\tau }_c\gg {\tau }_p\gg 2/\mathrm{\Gamma }$, where τ_p is the pumping time to reach the steady state. The length of the query pulse is limited by $2/\mathrm{\Gamma }<{\tau }_q\ll {\tau }_p$. For pulsed CPT excitation, the steady-state analysis is not applicable. Time-dependent density-matrix equations in Equation 1(1) $\begin{array}{l}\frac{d}{\mathit{dt}}\mathit{\rho }=-\frac{i}{\hslash }[\mathit{H\rho }-\mathit{\rho H}]+\mathcal{R}\mathit{\rho }\end{array}$(1) need to be solved for three successive time intervals (τ_c, T and τ_q) to calculate the time evolution of all the matrix elements.

As the preparation pulse is long, the steady state solution of the Bloch equations could be used as initial condition for determining the evolution at the later times. In the adiabatic regime where $\mathit{d}{\rho }_{33}(\mathit{t})/\mathit{dt}=\mathit{d}{\rho }_{13}(\mathit{t})/\mathit{dt}=\mathit{d}{\rho }_{23}(\mathit{t})/\mathit{dt}=0$, the short query pulse is well described using the ${\tau }_q\to 0$ limit. Then, the analytic solution of ${\rho }_{33}(\mathit{t})$ can be obtained by implementing an adiabatic approximation. This approximation is valid as the decay rate Γ is large compared to all other rates and the system can rapidly reach the equilibrium with the ground states. An analytical expression of the excited state population at the end of the interaction is given as [45]

(5) ${\rho }_{33}({\tau }_c+\mathit{T}+{\tau }_q)=\mathit{\alpha }{e}^{-\alpha \mathrm{\Gamma }{\tau }_q}[1-(1-e^{\alpha \mathrm{\Gamma }{\tau }_c})|\text{sec}(\mathit{\varphi })|\text{cos}(\mathrm{\Delta T}-{\varphi }_{\mathit{ls}})]$(5)

where $\mathit{\alpha }={\mathrm{\Omega }}^2/({\mathrm{\Gamma }}^2+3{\mathrm{\Omega }}^2+4{\delta }^2)$ represents the interaction with CPT pulses, $\mathrm{\Omega }=\sqrt{{\mathrm{\Omega }}_1^2+{\mathrm{\Omega }}_2^2}$ corresponds to the average Rabi frequency and ϕ_ls is the phase caused by the light shift. Exact steady-state line shapes and asymptotic profiles in the adiabatic pulsed regime is detailedly analysed in [46], and analytical results are in very good agreement with the simulations from Bloch’s equations (see Figure 3). A general analytical formula for the CPT-Ramsey interferometry is also valid for most situations with the arbitrary pulse sequences with time-varying detuning [47]. Equation (5)(5) ${\rho }_{33}({\tau }_c+\mathit{T}+{\tau }_q)=\mathit{\alpha }{e}^{-\alpha \mathrm{\Gamma }{\tau }_q}[1-(1-e^{\alpha \mathrm{\Gamma }{\tau }_c})|\text{sec}(\mathit{\varphi })|\text{cos}(\mathrm{\Delta T}-{\varphi }_{\mathit{ls}})]$(5) shows that the fringe-width Δν of CPT-Ramsey interference is decided by the free-evolution time T as $\mathrm{\Delta }\mathit{\nu }=1/(2\mathit{T})$. So one can narrow the linewidth via increasing the free-evolution time T, which has great advantages over the single-pulse CPT spectroscopy.

Figure 3. CPT-Ramsey interference fringes. Lines from the analytical expression and dots from simulation of Block’s equations. (b) Is the center part of (a) By zooming in the frequency span. Figure from [46].

2.2. Two-zone CPT-Ramsey interference with cold atoms

The two-zone CPT-Ramsey interference is implemented via exciting an atomic beam by means of CPT at two zones separated by a distance L. The approach is similar to the standard Ramsey interferometry with atomic beam directed through two spatially separated microwave cavities. In the first zone, the CPT effect prepares the atoms into the dark state. These atoms then evolve freely in the dark state for a time T until they arrive at the second zone. In the second zone, the phase of the atomic coherence is reading out by interacting with the same radiation fields. In order to make the atoms to experience equal microwave phases in the two zones, the optical path length between the zones should be the integer multiples of the wavelength of microwave transition [48]. The Ramsey interference phenomenon is observed by probing the fluorescence emitted in this second zone.

The two-zone CPT-Ramsey interference has been used as a frequency standard by employing a thermal beam of atoms [45,49–52] and also used to develop the chip-scale atomic beam clock based on microfabricated planar devices [53,54]. For atoms with an average speed v, the free-evolution time $\mathit{T}=\mathit{L}/\mathit{v}$, L is the distance between two zones. As the fringe-width Δν is inversely proportional to T, it needs to lengthen the distance between the two zones or lower the atom velocity to improve the spectral resolution. However, the average speed v is generally several hundred $\mathit{m}/\mathit{s}$ for the thermal atomic beam and the distance is limited by device’s size. Thus, there is a trade-off between the flight tube length and the resonance linewidth for relatively high velocity of atoms in the thermal beam. Although the narrow fringe-width of 650 Hz has been observed in the thermal atomic beam, the distance between the two zones is up to 30 cm [49], which is not suitable for developing compact quantum sensors.

The cold atomic beam employing the technique of laser cooling and trapping can generate a continuous stream of slow atoms. Two typical cold atom sources generating a continuous stream of slow atoms are shown in Figure 4. One of them termed low-velocity intense source (LVIS) is nearly identical to a standard vapor cell magneto-optical trap (MOT) with six orthogonal intersecting laser beams, except one of the six trapping laser beams has a narrow dark column in its center [55]. When the low-velocity atoms diffuse into the trap center, they enter the central column and are accelerated out of the trap by the counterpropagating laser beam. In the configuration, a rubidium atomic beam with a continuous flux of $5\times {10}^9$/s can be generated and its longitudinal velocity distribution is centered at 14 m/s with a full width at half maximum (FWHM) of 2.7 m/s.

Figure 4. Two typical cold atom sources generating a continuous stream of slow atoms. (a) Schematic of the low-velocity intense source (LVIS) system. The hole, located a distance z from the trap center, creates an extraction column through the trap center and causes atoms to accelerate out of the vapor cell magneto-optical trap. Figure is modified according to [55]. (b) Schematic of 2${\text{D}}^{+}$-MOT configuration. These so-called ioffe coils produce a two-dimensional quadrupole magnetic field for 2${\text{D}}^{+}$-MOT configurations. The atom beam leaves the vapor cell in the upward vertical direction through a 0.8 mm diameter hole. Figure from [56].

The other one termed 2${\text{D}}^{+}$-MOT is based on a combination of two-dimensional trapping and cooling with unbalanced optical molasses in the longitudinal direction [56]. It is an extension of the 2D-MOT by applying an additional pair of laser beams in the third direction. By adjusting these laser intensities unbalanced, the atoms are pushed out of the trapping center. A high flux of $9\times {10}^9$ rubidium atoms/s at a mean velocity of 8 m/s with a FWHM of 3.3 m/s were obtained. Compared with thermal atomic beam, the longitudinal peak velocity of cold atomic beam is less than that of thermal atomic beam with one order of magnitude. Meanwhile, its velocity distribution width is narrow. Hence, the CPT-Ramsey interference with cold atomic beam has a higher spectral resolution and shorter distance between the two zones than the thermal atomic beams. Along with the low temperature, it also has longer coherent time, which will increase the sensitivity of the quantum sensor.

A typical two-zone CPT-Ramsey interference with cold atoms is shown in Figure 5, which is similar to the Ramsey spectroscopy with stimulated Raman transitions [58]. Different from the most CPT experiments using D1 line interrogation, the interrogation with D2 line is used in this experiment to reduce the complexity of the laser system as a single laser can be the source for both the cooling beams and the CPT beams. The 2D-MOT is obtained by frequency shifting the cooling light red from the cycling transition of⁸⁷Rb atoms and creating the repumping light frequency with a fiber-coupled electro-optic modulator (EOM) driven at 6.58 GHz. The atomic beam is generated along the longitudinal axis of the cold atoms via partially reflecting the push beam that simultaneously provides some longitudinal cooling of the atoms. By tuning the push beam power, the peak velocity of the atomic beam can be changed from 5 m/s to 20 m/s.

Figure 5. Schematic of the two-zone CPT-Ramsey interference with cold atoms. (a) ⁸⁷Rb atoms are cooled in a 2D-MOT in the source cell, and the application of the push beam along the longitudinal direction narrows the velocity distribution and improves the beam flux. The atoms travel horizontally into the interrogation cell where they interact with the CPT light (“shown in green”) in two zones separated by 4.6 cm. The first zone creates the dark state, and the second zone probes the phase of the atomic coherence by reading out the atoms’ state. Above the second CPT zone are collection optics and a photomultiplier tube (PMT) that detects the fluorescent light. (b) CPT-Ramsey spectrum with cold atomic beam. The fringe width of 200 Hz agrees with the peak velocity of the atomic beam. Figure from [57].

The CPT-Ramsey interference is performed in the interrogation cell which includes two highly reflective-coated dielectric mirrors arranged in a configuration of a roof mirror. This retroreflecting optic both converts the polarization of the incident light from ${\sigma }^{+}$ to σ⁻ and reflect them back to form the double-Λ configurations, thereby improving the CPT resonance amplitude and reducing the impact of the Doppler shift. The two zones are separated by 4.6 cm and the CPT signal is collected using light collection optics and a photomultiplier tube (PMT) placed above the second zone. For a peak velocity 20 m/s of the atomic beam, the CPT-Ramsey fringes are shown in Figure 5(b). The fringe width is about 200 Hz, agrees with the free-evolution time $\mathit{T}=\mathit{L}/\mathit{v}=2.3$ ms. And more than 14 fringes are appeared, which implies a relatively narrow velocity distribution. Although narrower fringes can be obtained by lowing the peak velocity of atomic beam, the signal will be reduced as the size of the atomic beam is larger than the light beam in the second zone due to a wider velocity distribution. Thus, there is a trade-off between the fringe width and the signal-to-noise ratio (SNR).

2.3. Two-pulse CPT-Ramsey interference with cold atoms

Different from the two-zone CPT-Ramsey interference with two spatially separated CPT laser fields, the two-pulse CPT-Ramsey interference is implemented via exciting the atoms at two different times. This method has been used in alkali-metal vapor cells mixed with buffer gases to increase the coherent time [34,59,60]. However, the high-pressure buffer gases will induce the pressure shifts that altering the central frequency of the CPT-Ramsey spectroscopy, which affect the accuracy and stability of the quantum sensor. The cold atoms with temperature below 1 mK can overcome above shifts. Meanwhile the coherent time of cold atoms is much longer than that of thermal gases in vapor cells.

To implement the two-pulse CPT-Ramsey interference with cold atoms, one should first prepare the ensemble of cold atoms via laser cooling and trapping. The common method is using MOT followed by an optical molasses to cool the ensemble to a temperature of several µK. Then the free-fall ensemble is interrogated by two CPT pulses. When the atoms are probed along the vertical direction, the Doppler frequency shifts are induced under an acceleration of g due to gravity. In order to eliminate these shifts, the counterpropagating geometry should be used to average the phases of upwards and downwards propagating CPT fields via exciting the atoms in both directions [61]. Generally, the horizontal interrogation scheme is chosen to reduce the complexity of experiments. In this case, the interrogation time is limited by the flight time as the atoms are freely falling out of the CPT beam. The first pulse has a long length up to the order of microsecond to pump the ensemble into the dark state, while the second pulse is short enough to avoid any perturbation of the dark state. As the number of cold atoms is much less than that of vapor cell, the double-Λ configurations are usually employed to overcome the loss from trap states and maximize the CPT resonance amplitude [15–17,61–64].

The CPT-Ramsey fringes (Equation (5)(5) ${\rho }_{33}({\tau }_c+\mathit{T}+{\tau }_q)=\mathit{\alpha }{e}^{-\alpha \mathrm{\Gamma }{\tau }_q}[1-(1-e^{\alpha \mathrm{\Gamma }{\tau }_c})|\text{sec}(\mathit{\varphi })|\text{cos}(\mathrm{\Delta T}-{\varphi }_{\mathit{ls}})]$(5) ) could be obtained by collecting the fluorescence or detecting the CPT beam transmission during the second pulse. A typical experiment with fluorescence collection is shown in Figure 6. The single-beam mini MOT are used to minimize the experimental system [65]. The CPT fields with orthogonal polarization are used to form the lin$\perp$lin CPT scheme. After about 10^{7 87}Rb atoms are cooled and tapped in the mini MOT, the atomic ensemble is pumped by a 2-ms preparation pulse. In this process, the atom number could be determined via integrating the fluorescence photons as the emitted photons are exactly equal to the atom number during the CPT pumping process [62]. The CPT-Ramsey fringes are obtained by collecting the fluorescence during the second pulse and are shown in Figure 6(b) for the free-evolution time T = 6 ms. By dividing the second pulse fluorescence signal by the first pulse fluorescence signal, the SNR can be improved as the noise caused by the atom number fluctuation is suppressed.

Figure 6. The two-pulse CPT-Ramsey interference of lin$\perp$lin polarization scheme. (a) Experimental setup. The CPT laser fields are created by the −1th order beam of an acousto-optical modulator and the +1th order beam with orthogonal polarization. The CPT-Ramsey fringes are recorded by collecting the fluorescence during the second pulse. (b) CPT-Ramsey fringes with a free-evolution time T = 6 ms. The fringe width about 80 Hz is obtained. Figure from [62].

Comparing with the fluorescence collection, the detection of CPT beam transmission is more flexible and convenient as there is no need of optical collection system. Figure 7(a) shows the experimental setup of lin$||$lin polarization scheme. The CPT fields with parallel polarization can be easily generated by a single laser using a fiber-coupled EOM while the coherence of the CPT light is higher than that of optical phase-lock loop (OPLL), which increases the contrast of the CPT resonance [16]. Generally, a reference laser beam (also called as normalization laser beam) is used to reduce the influence of CPT laser intensity noise. A typical CPT-Ramsey fringes with the free-evolution time T = 16 ms is shown in Figure 7(b), the corresponding SNR is 180 in a 1-Hz bandwidth.

Figure 7. The two-pulse CPT-Ramsey interference of lin$||$lin polarization scheme. (a) Experimental setup. The CPT laser fields are created by a single laser beam using a fiber-coupled EOM with parallel polarization. The CPT-Ramsey fringes are recorded by detecting the CPT beam transmission during the second pulse. (b) CPT-Ramsey fringes with a free-evolution time T = 16 ms. The fringe width about 32 Hz is obtained. Figure from [16].

For both two-zone and two-pulse CPT-Ramsey interference with cold atoms, there are some common technologies. The optical system to prepare the cold atoms is the basic one. Generally, two different wavelengths of laser light are needed, one of them couples the cycling transition and the other one repumps the atoms back to the cycling transition. In the conventional cold-atom experiment, two laser sources with the frequency difference coupling the hyperfine splitting are requisite. For the CPT experiment, one laser usually serves as a source of the repumping and CPT light, even as the source of cooling, repumping and CPT light simultaneously to reduce the size of the optical system. Recently, the photonic-integrated-circuit-compatible laser system are proposed and employed to develop the compact quantum sensor [66]. The laser sources are usually frequency stabilized to the atomic transitions via the saturated absorption spectroscopy. As the bichromatic fields are used in the CPT experiment, the bichromatic Doppler-free spectroscopy with an increased absorption dip can improve the frequency stability [67–71]. Another common technology is the generation of cold atom sources. The MOT is the starting point for the CPT-Ramsey interference experiments. The conventional MOTs are formed at the center of a quadrupole magnetic field and the overlap region of six appropriately polarized red-detuned laser beams, which require a large number of optical components. Recent studies on the diffractive optics [72–74], metasurfaces [75,76] and photonic integrated circuits [77,78] have demonstrated the miniaturization of cold-atom platforms. Combination of the compact cold-atom platforms and the all-optical manipulation of CPT effect will promote the development of compact quantum sensors based on the CPT-Ramsey interferometry with cold atoms. And the grating MOT (gMOT) has been employed in the cold-atom CPT clock [18].

3. Multi-pulse CPT-Ramsey interferometry

Although the conventional CPT-Ramsey interferometry has a high resolution, there are two key issues to be addressed, especially for cold atoms with low atom number. On one hand, the central CPT-Ramsey fringe is difficult to identify from adjacent ones when the free-evolution time T increases. Since the central fringe is used for quantum sensing, this phenomenon can potentially create difficulties while engaging electronic servos to lock (or relock) to the peak of the central fringe. Thus, it becomes very important to suppress the non-central fringes and enhance the central fringe contrast to improve the sensitivity of the quantum sensors. Nonstandard CPT-Ramsey schemes have been studied to achieve high contrast Ramsey fringes [35–37,79]. An effective scheme is using multi-pulse interrogation to produce multi-pulse CPT-Ramsey interference. Applying multi-pulse CPT-Ramsey interferometry, the central fringe is constructively enhanced while adjacent fringes are destructively reduced.

On the other hand, the light shift induced by the CPT fields affects the accuracy of the CPT-Ramsey spectroscopy. In particular, atomic clocks are known to suffer on medium and long time scales from significant frequency instabilities, generally attributed to light-induced frequency-shift effects. Sophisticated Ramsey-based interrogation protocols using multi-pulse sequences have been proposed and demonstrated [27]. The main of these methods are based on a consecutive Ramsey sequences and each subsequence generates an error signal. The combination of these error signals can be used to apply frequency and phase correction.

3.1. Multi-pulse CPT-Ramsey interferometry and frequency filtering

To suppress the non-central fringes, a widely used and highly efficient way is inserting a CPT pulse sequence between the two CPT-Ramsey pulses to implement multi-pulse CPT-Ramsey interference. By employing the techniques of multi-pulse phase step or repeated query, the non-central fringes have been successfully suppressed.

Some experiments of multi-pulse CPT-Ramsey interference are performed under the $\mathit{\sigma }-\mathit{\sigma }$ configuration in atomic vapor cell. The multi-pulse phase-stepping differential CPT-Ramsey interferometry has been implemented in a compact ⁸⁷Rb atomic vapor cell under the $\mathit{\sigma }-\mathit{\sigma }$ configuration [35]. Due to the phase shift, a high contrast dispersive line shape in the central Ramsey fringe is achieved due to the constructive interference while other fringes are destructively reduced. The phase-stepping process requires precise adjustment of the relative phase between the bichromatic fields. In this process, any potential phase error could lead to a frequency error. Instead of phase-stepping, a repeated query technique in pulsed CPT may produce single-peaked Ramsey interference with high contrast [36]. This interrogation method only requires a simple modification of generating the pulse sequence.

For the double-Λ system with the lin$||$lin configuration, the transmission spectrum has been analytically obtained for arbitrary pulse lengths and pulse intervals. Notably, a mapping between the actions of CPT pulses and the reflection events of a Fabry-Pérot resonator has been given in Ref [37]. Through inserting a CPT pulse sequence between the two CPT-Ramsey pulses, similar to the constructive interference in a FPR, the central CPT-Ramsey fringe can be easily identified. In the five-level double-Λ system of N pulses, the final excited-state population can be analytically given as

(6) ${\rho }_{55}=\frac{{\mathrm{\Omega }}^2}{{\mathrm{\Gamma }}^2}+\frac{4{\mathrm{\Omega }}^2}{{\mathrm{\Gamma }}^2}\text{Re}[\mathit{\sigma }(\mathit{\delta })]$(6)

where the form of spin coherence is

(7) $\begin{array}{l}\mathit{\sigma }(\mathit{\delta })=\sum _{\mathit{l}=1}^{\mathit{N}}{\sigma }_{\mathit{N}-\mathit{l}+1}(\mathit{\delta })=\sum _{\mathit{l}=1}^{\mathit{N}}\mathit{f}(\mathit{\delta })[\prod _{\mathit{k}=\mathit{l}+1}^{\mathit{N}}\mathcal{R}(\mathit{k})]\mathcal{T}(\mathit{l}){\text{e}}^{-\text{i}\mathit{\delta }\sum _{\mathit{k}=\mathit{l}+1}^{\mathit{N}}\mathrm{\Delta T}(\mathit{k})}\end{array}$(7)

Exactly, the l-th pulse maps onto the $(\mathit{N}-\mathit{l}+1)$-th reflection event of an optical FPR. Here, $\mathit{f}(\mathit{\delta })=-\frac{{\mathrm{\Omega }}^2}{4\mathrm{\Gamma }(\text{i}\mathit{\delta }+\frac{{\mathrm{\Omega }}^2}{\mathrm{\Gamma }})}$, the reflection coefficient $\mathcal{R}(\mathit{l})={\text{e}}^{-\frac{{\mathrm{\Omega }}^2}{\mathrm{\Gamma }}\mathit{\tau }(\mathit{l})}$ and the transmission coefficient $\mathcal{T}(\mathit{l})\equiv 1-{\text{e}}^{-(\frac{{\mathrm{\Omega }}^2}{\mathrm{\Gamma }}+\text{i}\mathit{\delta })\mathit{\tau }(\mathit{l})}$. If the pulse length and the pulse interval are chosen as $\mathit{\tau }(\mathit{l})=\mathit{\tau }$ and $\mathrm{\Delta T}(\mathit{l})=\mathrm{\Delta T}$, $\mathit{\sigma }(\mathit{\delta })$ can be simplified as

(8) $\begin{array}{l}\mathit{\sigma }(\mathit{\delta })=\sum _{\mathit{l}=1}^{\mathit{N}}\mathit{f}(\mathit{\delta }){\mathcal{R}}^{(\mathit{l}-1)}\mathcal{T}{\text{e}}^{-\text{i}(\mathit{l}-1)\mathit{\delta }\mathrm{\Delta T}}\end{array}$(8)

with the reflection coefficient $\mathcal{R}={\text{e}}^{-\frac{{\mathrm{\Omega }}^2}{\mathrm{\Gamma }}\mathit{\tau }}$ and the transmission coefficient $\mathcal{T}=1-{\text{e}}^{-(\frac{{\mathrm{\Omega }}^2}{\mathrm{\Gamma }}+\text{i}\mathit{\delta })\mathit{\tau }}$. Obviously, the spin coherence Equation (8)(8) $\begin{array}{l}\mathit{\sigma }(\mathit{\delta })=\sum _{\mathit{l}=1}^{\mathit{N}}\mathit{f}(\mathit{\delta }){\mathcal{R}}^{(\mathit{l}-1)}\mathcal{T}{\text{e}}^{-\text{i}(\mathit{l}-1)\mathit{\delta }\mathrm{\Delta T}}\end{array}$(8) is analogous to the light transmission in an optical FPR.

Using identical pulses with equidistant intervals, a multi-pulse CPT-Ramsey interference via double-Λ CPT has been experimentally demonstrated with an ensemble of laser-cooled⁸⁷Rb atoms. Due to the constructive interference of spin coherence, the transmission spectrum appears as a comb of equidistant peaks in frequency domain and the distance between adjacent peaks is exactly the repeated frequency of the applied CPT pulses (see Figure 8). Thus, the central Ramsey fringe can be easily identified. When the external magnetic field is not too weak, each peak splits into two. This is caused by the small difference of absolute value between the two g factors of two ground hyperfine levels. Due to the high resolution of multi-pulse CPT-Ramsey interference, this splitting can be clearly measured. It is worth noting that this splitting is exactly linear with the magnetic field strength and can be used for measuring a magnetic field without involving magneto-sensitive transitions.

Figure 8. (a) Energy levels of ⁸⁷Rb D1 line transitions under the lin$||$lin configuration. (b) The temporal analog of FPR. (c) Experimental transmission signals for different schemes including single-pulse, two-pulse and multi-pulse CPT-Ramsey spectra of N equidistant pulses with a length $\mathit{\tau }=$2 µs into the integration time of 0.5 ms. Figure from [37].

3.2. CPT-Ramsey spectroscopy with composite pulse sequences

For conventional CPT-Ramsey interrogation, there are residual frequency shifts induced by the CPT fields during the interrogation pulses. These interrogation-related shifts (light shifts) originate from a phase shift ϕ_ls accumulated during the interrogation pulses and are inversely proportional to the interrogation time as $f_s=-{\varphi }_{\mathit{ls}}/2\mathit{\pi T}$. In order to compensate the light shifts, Ramsey Spectroscopy using composite pulse sequences is investigated. The hyper-Ramsey spectroscopy, which utilizes pulses individually tailored in duration, phase and frequency, has been proposed to eliminate light shifts [31]. In addition, the generalized autobalanced Ramsey spectroscopy (GABRS) can also be used to eliminate light shifts [29]. The main originality of these methods is the utilization of Ramsey sequences with two different evolution periods. Accordingly, two feedback loops are used to null the light shifts and stabilize the clock frequency. Usually, one loop is used to stabilize the local oscillator (LO) frequency to the atomic resonance, while the second loop feeds back to a secondary variable and ultimately compensates for light shifts. The GABRS can be implemented with different secondary variables including added relative phase shifts between Ramsey pulses, external frequency-step compensation, and variable second-pulse duration.

The autobalanced Ramsey (ABR) interrogation protocol has been experimentally implemented onto a Cs vapor-cell CPT clock. The method is based on the alternation of two successive Ramsey-CPT sequences with unequal free-evolution times and the subsequent management of two interconnected phase and frequency servo loops. Due to a relevant reduction of the clock-frequency sensitivity to laser-power variations, one may achieve a short-term fractional frequency stability at the level of $3.1\times {10}^{-13}{\tau }^{-1/2}$, averaging down to the level of $6\times {10}^{-15}$ at 2000 s integration time [80]. One issue when using the ABR-CPT protocol is that the clock short-term frequency stability is degraded due to the relaxation of the CPT coherence [10]. The explanation is that when the repetition rate of the successive Ramsey sequences is faster than the CPT coherence relaxation rate, the atomic signal level detected at a given CPT pulse depends also on the previous CPT pulses. So it induces a frequency-error in the light-shift estimation in the ABR-CPT regime. In order to solve this issue, the further implementation of a symmetric ABR-CPT interrogation sequence allows the generation of two successive offsets with equal modulus and opposite sign that cancel each other. This yields a gain of a factor 2 on the clock short-term stability [30]

Sophisticated Ramsey-based interrogation protocols using composite laser pulse sequences have also been demonstrated in cold-atom CPT clocks. The Ramsey spectroscopy with displaced frequency jumps (DFJR) has been reported in Ref [64,81]. In a Ramsey clock, by sampling bilateral half-maximum points of the central Ramsey fringe, a zero-crossing error signal can be derived by subtraction of the two measurements. One option for the generation of the error signal is known as frequency jumps, which is to jump the LO frequency to $f_{\mathit{c}}-1/(4\mathit{T})$ ($f_{\mathit{c}}+1/(4\mathit{T})$) from the estimated clock frequency f_c. The light shifts can be eliminated by applying frequency jumps of different magnitude to the right $(f_{\mathit{c}}+(1/(4\mathit{T})+\mathit{\alpha }/\mathit{T}))$ and left $(f_{\mathit{c}}-(1/(4\mathit{T})-\mathit{\alpha }/\mathit{T}))$ sides of the fringe such that the error signal steers the clock to the nonshifted frequency. The interrogation asymmetry is denoted by $\mathit{\alpha }/\mathit{T}$, where α is the concomitant control parameter in the DFJR scheme. The DFJR scheme consists of a composite Ramsey sequence involving two cycles with a long evolution period T_L and two cycles with a short evolution period T_S, as shown in Figure 9. In the long evolution-period cycles, the sampling frequencies are $f_{\mathit{c}}+(1/(4T_{\mathit{L}})+\mathit{\alpha }/\mathit{T})$ and $f_{\mathit{c}}-(1/(4T_{\mathit{L}})-\mathit{\alpha }/\mathit{T})$, while for the short evolution period cycles the corresponding frequencies are $f_{\mathit{c}}+(1/(4T_{\mathit{S}})+\mathit{\alpha }/\mathit{T})$ and $f_{\mathit{c}}-(1/(4T_{\mathit{S}})-\mathit{\alpha }/\mathit{T})$. Thus, one control parameter (the clock frequency f_c) is the same for both evolution periods, while the other control parameter (α) causes a frequency displacement that scales with the evolution period. This allows one to implement two control parameters combined in a single physical variable (the LO frequency). The error signal from the long evolution-period cycles ɛ_L is used to steer the clock frequency, while the error signal from the short evolution-period cycles ɛ_S is used to steer α. The only steady-state solution that nulls both error signals occurs when the clock frequency is on resonance, which results in a clock frequency free from the influence of interrogation-related shifts. The advantage of DFJR scheme is that only LO frequency is used to control both servo loops, simplifying the implementation and avoiding noise associated with controlling the LO phase. They have demonstrated that the DFJR scheme can reduce the sensitivity of the clock frequency to variations of the light shifts by more than an order of magnitude compared with the standard Ramsey interrogation.

Figure 9. (a) Illustration of light shifts and their mitigation using the DFJR method. (b) The DFJR sequence that is composed of four consecutive Ramsey cycles−two with a long evolution period and two with a short evolution period. Figure from [64].

4. Applications

The CPT phenomenon is a result of destructive quantum interference between different transition paths. The characteristic of all-optical manipulation makes it more suitable for developing chip-scale quantum sensors [20,54,82]. However, most of practical quantum sensors based on CPT use alkali-metal vapor cells mixed with the buffer gases that induce the pressure shifts. The CPT-Ramsey interferometry with cold atoms can circumvent the issue, especially the multi-pulse CPT-Ramsey interferometry can improve the contrast and accuracy of the spectrum.

An application of CPT-Ramsey interferometry is the cold-atom CPT clock, which is proposed towards a compact cold-atom frequency standard [61]. Using the cold-atom technique, the high-pressure shift can be canceled, and the coherence time of the atoms can be significantly increased. The completeness of dark state formation of cold atoms CPT interrogation is much better than that in vapor cell-based interrogation. So the long-term frequency stability of cold-atom CPT clocks can be greatly improved compared with the vapor cell-based CPT clock. The high-performance CPT clocks based on laser-cooled atoms have been demonstrated [15–17] and their long-term stability can reach $1.8\times {10}^{-13}$ at 20,000 s integration time (see Figure 10).

Figure 10. Cold-atom CPT clock. (a) The architecture of experimental apparatus. (b) Frequency stability of the cold-atom CPT clock. Figure from [17].

Benefit from the flat diffractive optic, gMOTs show great potential as a cold-atom source for integrated, portable devices. The combination of gMOT and CPT-Ramsey interferometry will drastically reduce the size, weight, power and complexity of the cold-atom clocks. An ⁸⁷Rb gMOT-based cold-atom microwave clock has been built as a test-bed to investigate the combination of the gMOT with CPT-Ramsey interferometry (see Figure 11). The gMOT is formed from a single incident beam and its inward diffracted orders directed onto the grating chip. With the removal of the additional five cooling beams for conventional MOTs, the gMOT can be miniaturised without significantly compromising optical access. The CPT-Ramsey fringes with an approximate SNR of 100 have been observed in this apparatus. The frequency stability of the clock reach to $2\times {10}^{-11}/\sqrt{\mathit{\tau }}$, which is close to the stability of conventional cold-atom CPT clocks.

Figure 11. Cold-atom CPT clock based on gMOT. (a) Schematic of the gMOT with CPT detection. (b) Measured Allan deviation curves with a T = 10 ms free evolution time. Inset: an example T = 10 ms fringe, where each point is a single experimental run. Figure from [18].

Nevertheless, taking into account the repetition rate of the clock operation, the atomic cloud is normally cooled by tens of milliseconds that give rise to a lower atom number than that of vapor cell. So far, the cold-atom CPT clocks have a lower short-term stability than that of vapor cell-based CPT clocks. By applying the repeated query pulses, the vapor cell-based CPT clock has demonstrated a better short-term stability by a factor of 2.2 compared to the conventional CPT-Ramsey interferometry [36]. We anticipate the short-term stability of cold-atom CPT clocks will also be improved in virtue of the multi-pulse CPT-Ramsey interferometry.

A potential application of the CPT-Ramsey interferometry with cold atoms is the magnetometer, which can reach a high absolute accuracy as it directly measures the hyperfine splitting between two magneto-sensitive Zeeman states. The CPT magnetometer based on alkali-metal vapor cell has been applied to measure the vector of the Earth’s magnetic field profiting from its outstanding absolute accuracy [83]. As the CPT-Ramsey interferometry with cold atoms has a high spectral resolution, the combination of CPT-Ramsey interferometry and compact cold-atom system will promote the development of absolute magnetic field measure. In addition, we propose a quantum double lock-in amplifier arming to extract an alternating signal within strong noise background [84]. This protocol could be realized in virtue of the CPT-Ramsey interferometry in a five-level double-Λ CPT system, in which each Λ structure acts as a quantum mixer. Magnetometer based on CPT-Ramsey interferometry with cold atoms will be beneficial for developing practical quantum sensing technologies.

5. Conclusion and perspective

In this article, we provide a concise overview of CPT-Ramsey interferometry employing cold atoms. Unlike traditional methods utilizing a microwave cavity, CPT utilizes optical interrogation of the atomic transitions in alkali-metal atoms. This approach offers the advantages of low power consumption and a compact size, making it suitable for the construction of practical quantum sensors. Ramsey interferometry, a key component of this technique, involves the interrogation of atomic transitions using separated oscillatory fields, resulting in high-precision spectroscopy. Specifically, the application of multi-pulse Ramsey interferometry enhances both contrast and accuracy in spectroscopic measurements. Leveraging the extended coherence time of cold atoms further allows for improvements in the sensitivity and accuracy of quantum sensors.

There are various factors impeding the achievement of the quantum projection noise limit in quantum sensors utilizing CPT-Ramsey interferometry with cold atoms. The existing limitations stem from a combination of residual laser intensity noise, electronic detection noise, and photon shot noise. Employing multi-pulse schemes proves beneficial in enhancing the signal-to-noise ratio of CPT-Ramsey fringes. Additionally, exploiting correlations between measurements with different interrogation times can further increase sensitivity, with well-designed Bayesian estimation algorithms demonstrating the potential for sensitivity improvement to the sub-standard quantum limit, scaling as $\propto T^{-\mathit{\alpha }}$ [85]. Moreover, the application of spin squeezing to CPT-Ramsey interferometry may further improve the sensitivity of cold-atom quantum sensors [86].

Furthermore, significant advancements in diffractive optics, metasurfaces, and photonic integrated circuits contribute to the compactness of cold-atom platforms. Simultaneously, microfabricated photonic integrated circuit technology offers a robust and reliable solution for chip-scale laser systems [87]. The integration of CPT, Ramsey interferometry, chip-scale laser systems, and compact cold atoms holds promise for advancing practical quantum sensors.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the National Key Research and Development Program of China [2022YFA1404104]; the National Natural Science Foundation of China [12025509, 12104521], and the Key-Area Research and Development Program of GuangDong Province [2019B030330001].