Segment-based coancestry, additive relationship and genetic variance within and between the Norwegian and the Swedish Fjord horse populations

Figures & data

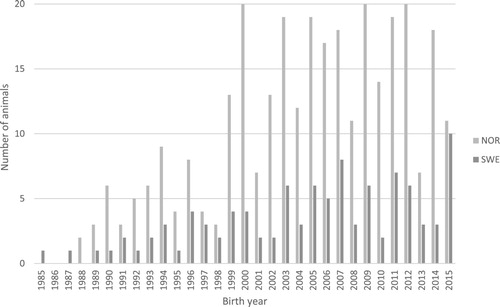
Figure 1. Average coefficient of inbreeding (F) per birth year and number of animals in the pedigree per birth year for the Norwegian Fjord horse population over the period 1857–2016.

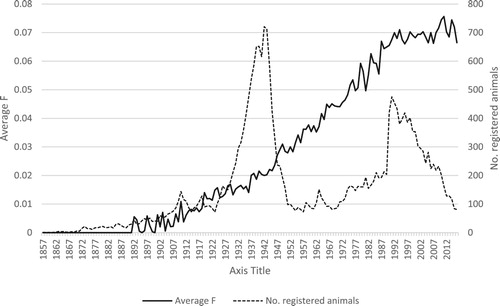
Figure 2. The age distribution of the animals contributing with genotype data (recorded December 2015 to March 2016), shown through the number of animals born per year in the Norwegian (N = 311) and the Swedish Fjord horse populations (N = 102).

Table 1. Number of Norwegian (NOR) and Swedish (SWE) individuals passing the genotype tests (reference population) and their estimated complete generation equivalent and generation interval per population.

	NOR	SWE
# animals in reference population	311	102
Complete generation equivalent (CGE)	12.7	11.6
Generation interval^a	9.1	11.6

^aCalculated from a subset of the genotyped horses (224 NOR and 103 SWE).

Table 2. Average and range of the inbreeding coefficient based on pedigree (F_ped), and of coancestry coefficients from pedigree (ƒ_ped) and shared genomic segments (ƒ_seg;≥ 100 kb) in the Norwegian (NOR) and the Swedish (SWE) populations.

	Mean			Range
	NOR	SWE	NORxSWE	NOR	SWE	NORxSWE
Fped	0.077	0.052	–^a	0.005–0.191	0.0008–0.129	–^a
ƒped	0.082	0.065	–^a	0.030–0.344	0.017–0.311	–^a
ƒseg	0.141	0.119	0.115	0.060–0.439	0.055–0.379	0.047–0.396

^aNot calculated because a unique identity does not exist across the populations in Norway and Sweden.

Table 3. Intercept (β₀) and slope (β1) of $\ln (1-Y{)}_i=y_i={\text{β}}_0+{\text{β}}_1\cdot \mathrm{l}\mathrm{n}(1-X{)}_i+e_i,$ where X is the kinship coefficient from genomic segments (ƒ_seg ≥ 100 kb) and X is the corresponding coefficient from pedigree (ƒ_ped), in the Norwegian (NOR) and the Swedish (SWE) populations. The coefficient of determination (R²) of the regression model is also included.

Y	X	β0		β1		R^2
		NOR	SWE	NOR	SWE	NOR	SWE
ƒseg	ƒped	−0.068	−0.062	0.983	0.952	0.636	0.819

Table 4. Regression coefficients with belonging standard errors (s.e.) from the regression: y_i = b₀ + b₁X_i + e_i, where y_i is either 1 − F_ped (F_ped being individual inbreeding coefficient from pedigree), or 1 − f_seg (f_seg being coancestry coefficient from shared genomic segments (≥100 kb) for animals born ≤10 years apart), and X_i denotes the individual birth year (average birth year of the pair), in the Norwegian (NOR), the Swedish (SWE), and in the joint population (All). Also, the calculated effective population size $N_e=1/2(\mathrm{\Delta }F=1-e^{b_1})$ with a corresponding confidence interval from $\mathrm{\Delta }F=1-e^{b_1\pm 1.96\mathrm{s}.\mathrm{e}.}$ for the Norwegian (NOR), the Swedish (SWE), and the joint population (All).

	b1 ± s.e.			Ne (confidence interval)
	NOR	SWE	All	NOR	SWE	All
Fped	−7.7·10^−4 ± 5.3·10^−6	−1.6·10^−4 ± 3.1·10^−6	–^a	71 (70–72)	269 (259–279)	–^b
ƒseg	−8.7·10^−4 ± 5.0·10^−5	−0.4·10^−4 ± 1.7·10^−4	−5.6·10^−4 ± 4.0·10^−5	63 (57–72)	1136 (119 – ∞)	87 (77–100)

^aCalculated from a complete pedigree traced back to the founders from the 311 Norwegian and the 102 Swedish horses with a complete generation equivalent of 12.7 and 11.6, respectively, using the software EVA (Berg et al., 2006).

^bNot calculated because a unique identity does not exist across the populations in Norway and Sweden.

Berg, P., Nielsen, J. & Sørensen, M. K. (2006). EVA: Realized and predicted optimal genetic contributions. Proceedings of the 8th World Congress on Genetics Applied to Livestock Production, August 13–18, Belo Horizonte, Minas Gerais, Brazil.

 Google Scholar