A Causal Framework for the Comparability of Latent Variables

Figures & data

Figure 1. Simple DAG of a measurement model where the observed variables $Y_1,$ $Y_2,$ and $Y_3$ are caused by a latent common factor C and latent unique error terms $E_1,$ $E_2,$ and $E_3.$

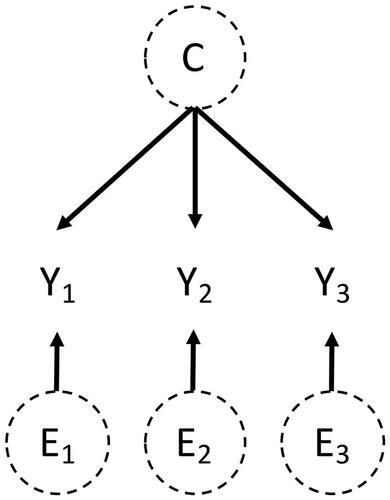
Figure 2. Simple path diagram of a measurement model. (a) LISREL style: only error variances are depicted by an arrow without a node pointing into all endogeneous variables (here: the observed variables); (b) RAM style: variances of both endogeneous and exogeneous variables are depicted by a double-headed arrow-loop (here: error variances and variances of the latent variables).

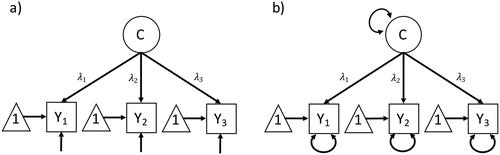
Figure 3. DAG with a selection node pointing into the observed variables. (a) Adaptation of Figure 6c in Deffner et al. (2022) where only one observed variable Y is shown; (b) DAG of the complete measurement model of IB = impartial beneficence where the selection node points into potentially all observed variables $Y_{1-5}$ (depicted by the dotted box around the observed variables).

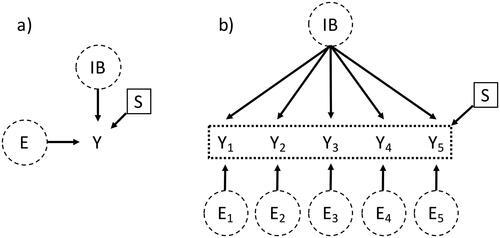
Figure 4. Pairs of measurement models of IB (impartial beneficence) for which measurement invariance does not hold between the two groups. (a) violation of configural invariance (violation of configural invariance due to different number of latent variables between groups is not displayed); (b) violation of metric invariance (assuming standardized data); (c) violation of scalar invariance; (d) violation of residual invariance (assuming unstandardized data). Parameters that differ between groups are highlighted in blue.

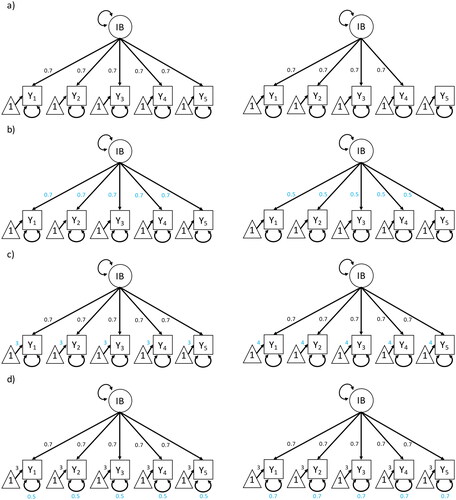
Figure 5. DAG with a selection node pointing into the observed covariate Age which influences all observed variables $Y_{1-5}$ (depicted by the dotted box around the observed variables).

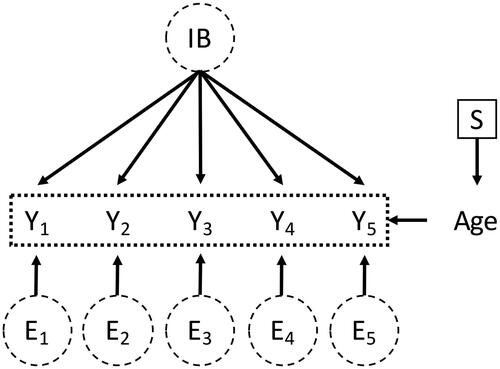
Table 1. Results of moderated non-linear factor analysis for the toy example.

Item	${\tau }_0$	$b_{\mathit{\text{Region}}}$	$b_{\mathit{\text{Age}}}$	${\Lambda }_0$	$D_{\mathit{\text{Region}}}$	$D_{\mathit{\text{Age}}}$
Item 1	−0.07	0.15	−0.05	1.04	−0.05	0.00
Item 2	−0.08	0.03	−0.03	0.80	−0.07	0.35
Item 3	−0.06	0.12	−0.04	0.75	0.01	0.27
Item 4	−0.09	0.06	−0.04	0.74	−0.03	0.30
Item 5	−0.04	0.04	−0.05	0.73	0.04	0.30

Note. ${\tau }_0$ = Baseline intercepts, $b_{\mathit{\text{Region}}}$ = (Additive) Effects of covariate Region on baseline intercepts, $b_{\mathit{\text{Age}}}$ = (Linear) Effects of covariate Age on baseline intercepts, ${\Lambda }_0$ = Baseline loadings, $D_{\mathit{\text{Region}}}$ = (Additive) Effects of covariate Region on baseline loadings, $D_{\mathit{\text{Age}}}$ = (Linear) Effects of covariate Age on baseline loadings. Effects of Region and Age on other model parameters, e.g., residual variances, are not reported here. Reference category of Region is Eastern. The loading of item 1 was simulated as 1 for identification purposes.

Table 2. Results of ${\chi }^2$-difference tests between the configural, metric, and scalar moderated non-linear factor analyses for the simulated example.

Comparison	$\Delta -2\mathit{\text{LL}}$	$\Delta \mathit{\text{df}}$	p-Value
Configural vs. metric	290.39	10.00	0.00
Metric vs. scalar	−113.63	6.00	1.00

Note. $\Delta -2\mathit{\text{LL}}$ = difference in −2 times the log-likelihood of the models, $\Delta \mathit{\text{df}}$ = Difference in degrees of freedom. A p-value of 0 means that it is $<0.005.$

Table 3. Results of multi-group confirmatory factor analysis for the empirical example between regions Western and Eastern.

Model	df	${\chi }^2$	$\Delta {\chi }^2$	$\Delta \mathit{\text{df}}$	p-Value	RMSEA
Configural	10	104.36	–	–	–	0.06
Metric	14	142.72	38.36	4	0.00	0.06
Scalar	18	373.54	230.83	4	0.00	0.08

Note. df = Degrees of freedom, ${\chi }^2$ = Value of the test statistic, $\Delta {\chi }^2$ = Difference in values of the test statistics, $\Delta \mathit{\text{df}}$ = Difference in degrees of freedom, RMSEA = Root mean square error of approximation. A p-value of 0 means that it is $<0.005.$

Table 4. Results of moderated non-linear factor analysis for the empirical example.

Item	${\tau }_0$	$b_{\mathit{\text{Region}}}$	$b_{\mathit{\text{Age}}}$	${\Lambda }_0$	$D_{\mathit{\text{Region}}}$	$D_{\mathit{\text{Age}}}$
Item 1	3.68	0.22	0.00	0.96	−0.16	0.00
Item 2	3.21	0.24	0.01	1.41	0.02	−0.01
Item 3	4.26	−0.19	0.01	0.68	0.12	0.00
Item 4	2.77	0.49	0.02	0.82	0.10	0.00
Item 5	3.42	0.05	0.01	1.17	−0.10	0.00

Note. ${\tau }_0$ = Baseline intercepts, $b_{\mathit{\text{Region}}}$ = (Additive) Effects of covariate Region on baseline intercepts, $b_{\mathit{\text{Age}}}$ = (Linear) Effects of covariate Age on baseline intercepts, ${\Lambda }_0$ = Baseline loadings, $D_{\mathit{\text{Region}}}$ = (Additive) Effects of covariate Region on baseline loadings, $D_{\mathit{\text{Age}}}$ = (Linear) Effects of covariate Age on baseline loadings. Effects of Region and Age on other model parameters, e.g., residual variances, are not reported here. Reference category of Region is Eastern.

Table 5. Results of ${\chi }^2$-difference tests between the configural, metric, and scalar moderated non-linear factor analyses for the empirical example.

Comparison	$\Delta -2\mathit{\text{LL}}$	$\Delta \mathit{\text{df}}$	p-Value
Configural vs. metric	44.66	10.00	0.00
Metric vs. scalar	276.26	6.00	0.00

Note. $\Delta -2\mathit{\text{LL}}$ = difference in –2 times the log-likelihood of the models, $\Delta \mathit{\text{df}}$ = Difference in degrees of freedom. A p-value of 0 means that it is $<0.005.$

Deffner, D., Rohrer, J. M., & McElreath, R. (2022). A causal framework for cross-cultural generalizability. Advances in Methods and Practices in Psychological Science, 5. https://doi.org/10.1177/25152459221106366

 PubMedGoogle Scholar