Fair and efficient ride-scheduling: a preference-driven approach

Figures & data

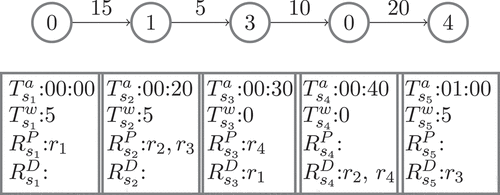
Table 1. Overview of the model’s formal notation.

Symbols	Description
$r_i$	Rider $\mathit{i}$
$l_d(r_i)$	Departure location for $r_i$
$l_a(r_i)$	Arrival location for $r_i$
$T_d^{\ast }(r_i)$	Preferred departure time for $r_i$
$T_a^{\ast }(r_i)$	Preferred arrival time for $r_i$
$T_d(r_i)$	Allocated departure time for $r_i$
$T_a(r_i)$	Allocated arrival time for $r_i$
$\mathit{s}(r_i)$	Status for $r_i$, which can be $\mathit{onboard}$ or $\mathit{onground}$
${\beta }_{r_i}$	Patience parameter for $r_i$
$\mathit{G}(\mathit{L},\mathit{E})$	Fully connected graph with locations $\mathit{L}$ and edges $\mathit{E}$
$l_i\in \mathit{L}$	Location $\mathit{i}$
$\mathit{e}(l_i,l_j)\in \mathit{E}$	Edge between $l_i$ and $l_j$
$\mathit{w}(l_i,\mathit{l}\mathit{j})$	Travel Time between station $l_i$ and station $l_j$
$\mathcal{S}$	Sequence of TourNodes
$\mathit{Pos}(\mathit{S})$	Insertion positions of $\mathcal{S}$
$s_i$	TourNode at the $\mathit{i}$-th position of $\mathcal{S}$
$l_{s_i}$	Location at $s_i$
$T_{s_i}^{\mathit{a}}$	Arrival time at $s_i$
$T_{s_i}^{\mathit{w}}$	Waiting time at $s_i$
$T_{s_i}^{\mathit{d}}$	Departure time at $s_i$
$R_{s_i}^{\mathit{P}}$	Set of riders picked up at $s_i$
$R_{s_i}^{\mathit{D}}$	Set of riders dropped off at $s_i$

Figure 1. Solution model.

Table

Algorithm 1: Randomised Greedy Algorithm

Table

Algorithm 2: Randomised Greedy ++

Figure 2. Iterative Voting procedure.

Table

Algorithm 3: Iterative Voting

Table 2. Bus service parameters.

Parameter	Value
Service Hours	$24$
Average Speed	$13\mathrm{km}/\mathrm{h}$

Table 3. Rider parameters. The first row refers to the values of the beta distribution; the second row describes the sampling method for the pick up and drop off locations; the third row shows the number of riders for each experiment.

Parameter	Value
$(\mathrm{alpha},\mathrm{beta})$	$[(10,10),(10,2),(2,10),(1/2,1/2)]$
Spatial preferences	$[\mathrm{uniform},10\mathrm{hotspots},20\mathrm{hotspots}]$
Number of Riders	$[25,50,75,100,125,150,175,200]$

Table 4. Time frames.

Service Type	Time Frame
Midnight Rides	[0, 420]
Morning Peak	[420, 560]
Working Hours	[560, 1020]
Evening Peak	[1020, 1140]
Night Rides	[1140, 1440]

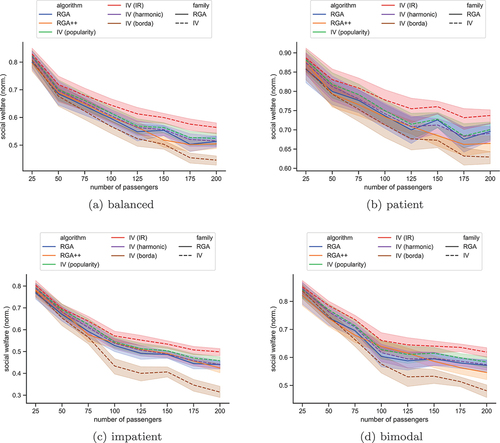
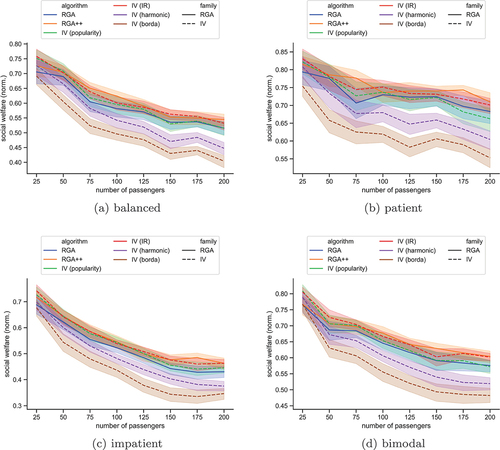
Figure 3. The social welfare, normalized by the number of passengers in the scenario without hotspots, for each algorithm. The plots show bands of $95\mathrm{\%}$ confidence intervals.

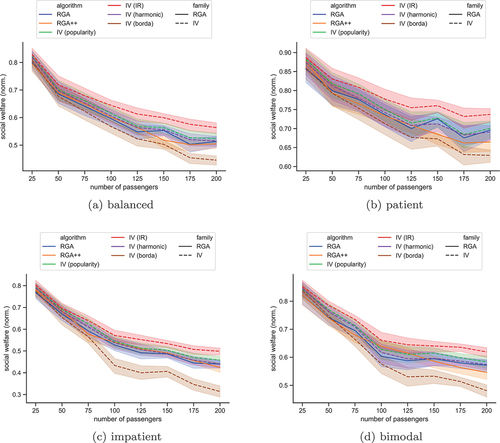
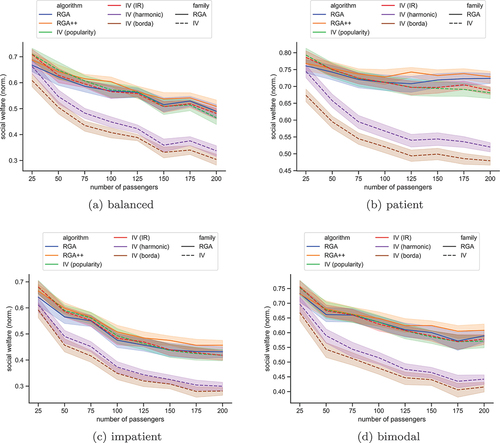
Figure 4. The social welfare, normalized by the number of passengers, in the scenario with $10$ hotspots, for each algorithm. The plots show bands of $95\mathrm{\%}$ confidence intervals.

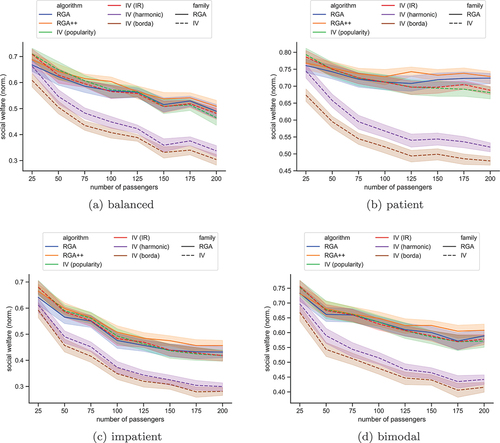
Figure 5. The social welfare, normalized by the number of passengers, in the scenario with 20 hotspots, for each algorithm. The plots show bands of $95\mathrm{\%}$ confidence intervals.

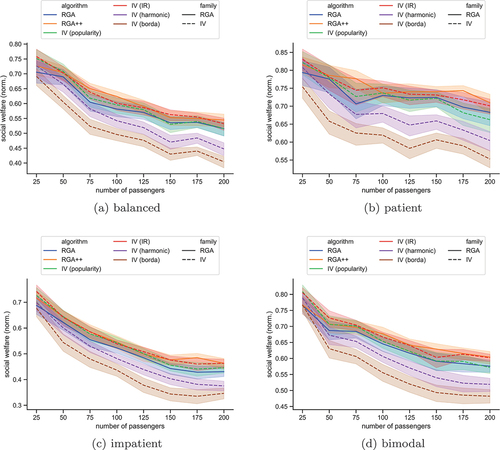
Figure 6. The mean Gini index in the scenario without hotspots, for each algorithm. The plots show bands of $95\mathrm{\%}$ confidence intervals.

Figure 7. The mean Gini index in the scenario with $10$ hotspots, for each algorithm. The plots show bands of $95\mathrm{\%}$ confidence intervals.

Figure 8. The mean Gini index in the scenario with 20 hotspots for each algorithm. The plots show bands of $95\mathrm{\%}$ confidence intervals.