A dynamic closure modeling framework for large eddy simulation using approximate deconvolution: Burgers equation

Figures & data

Figure 1. Transfer functions of the sixth-order compact Padé filters for various free filtering parameters.

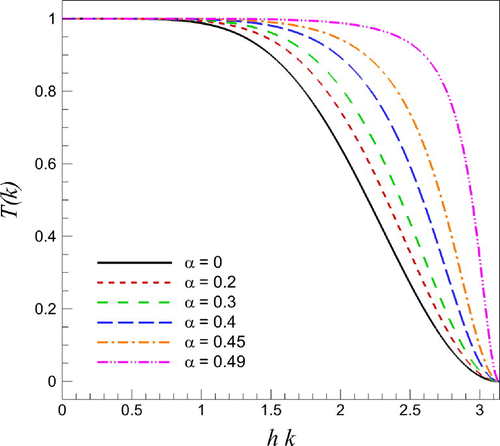
Figure 2. Conservative formulation results for solving the Burgers equation initiated by the single-mode sine wave: (a) time evolution by DNS with resolution of $N=32768$; (b) under-resolved numerical simulation (UNS); (c) dynamic Smagorinsky model (D-SMA); and (d–f) the proposed dynamic AD model (D-AD) with various orders of Q. In (b–f), we present the final snapshots at time $t=2.5$ using resolutions of 512, 1024, and 2048 where the results for 512 and 1024 resolutions are shifted in the x-axis for the purpose of illustration.

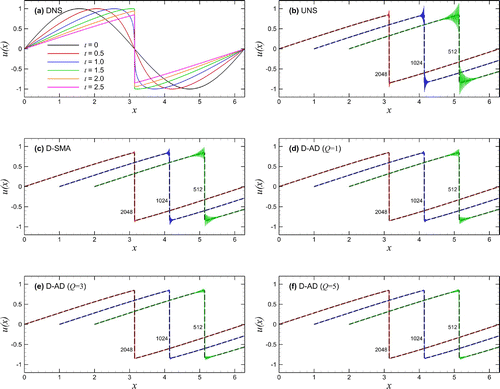
Figure 3. Conservative formulation for the shock formation problem initiated by a single-mode sine wave using 512 grid points: a comparison for the time evolution of the dissipation rate (left) and its close-up for local enlargement (right).

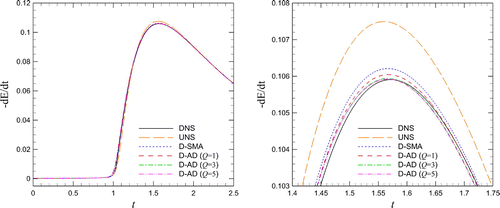
Figure 4. Skew-symmetric formulation simulation results for solving the Burgers equation initiated by the single-mode sine wave: (a) time evolution by DNS with resolution of $N=32768$; (b) under-resolved numerical simulation (UNS); (c) dynamic Smagorinsky model (D-SMA); and (d–f) the proposed dynamic AD model (D-AD) with various orders of Q. In (b–f), we present the final snapshots at time $t=2.5$ using resolutions of 512, 1024, and 2048 where the results for 512 and 1024 resolutions are shifted in the x-axis for the purpose of illustration.

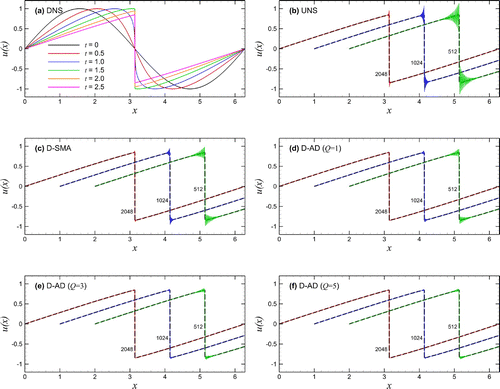
Figure 5. Skew-symmetric formulation for the shock formation problem initiated by a single-mode sine wave using 512 grid points: a comparison for the time evolution of the dissipation rate (left) and its close-up for local enlargement (right).

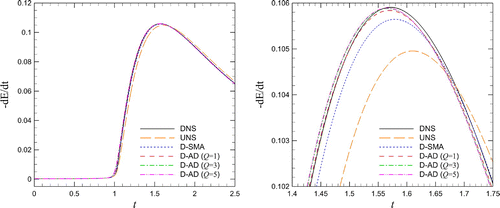
Figure 6. A comparison of energy spectra for $N=512$ resolution results at time $t=2.5$ obtained by the conservative (left) and skew-symmetric (right) formulations for the shock formation problem initiated by a single-mode sine wave.

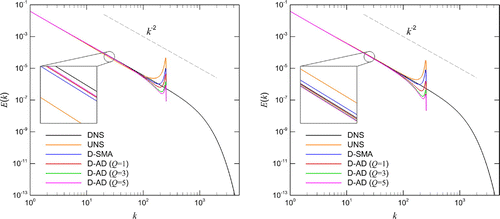
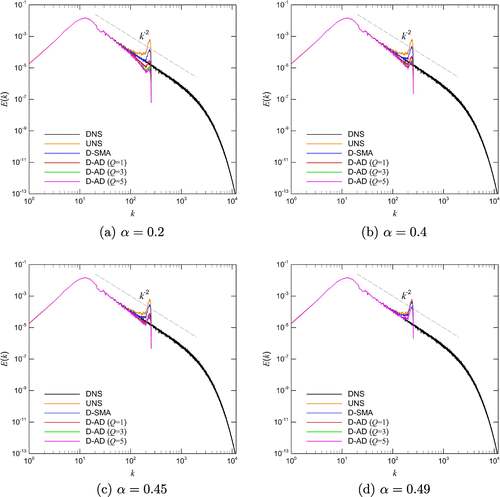
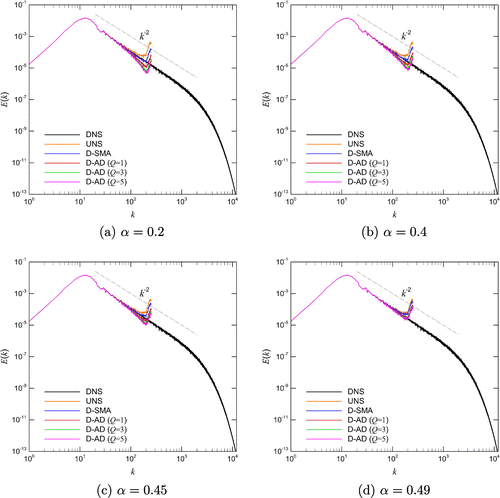
Figure 7. Intercomparison of $N=512$ resolution results for solving the Burgers equation initiated by the single-mode sine wave using the conservative formulation (left column) and the skew-symmetric formulation (right column). Note that the simulation results for UNS, D-SMA, D-AD ($Q=3$), and D-AD ($Q=5$) are shifted in x-axis for the purpose of illustration.

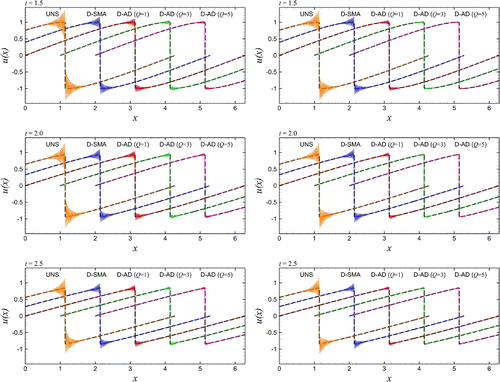
Figure 8. Space–time solutions of the Burgers equation using three different initial conditions generated from Equation (40(40) $$\begin{array}{c}\hfill E(k)=\frac{2}{3\sqrt{\pi }}\frac{k^4}{k_0^5}{e}^{-{(k/k_0)}^2},\end{array}$$(40) ).

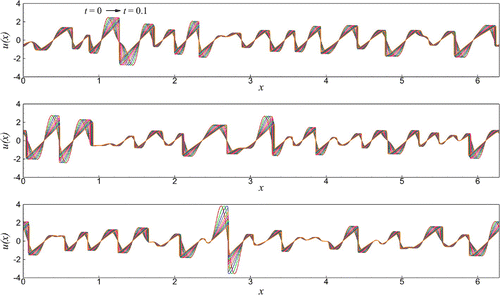
Figure 9. Time evolution of the energy spectrum for the Burgers turbulence problem based upon the ensemble average of 64 sample fields obtained by DNS ($N=32768$) (left), and a comparison of energy spectra at time $t=0.05$ obtained by various spatial resolutions ranging from $N=512$ to $N=32768$ (right).

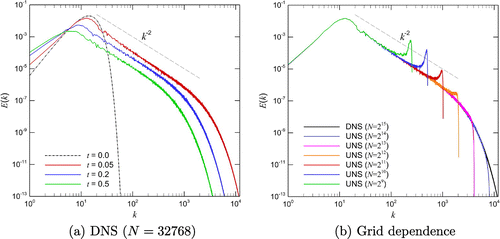
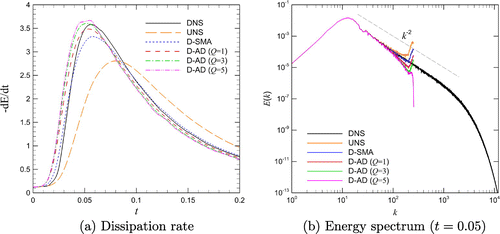
Figure 10. Results for the SGS modeling of the Burgers turbulence problem obtained using $N=512$ resolution with the conservative formulation of the nonlinear term: time evolution of the total dissipation rate (left) and energy spectra at time $t=0.05$ (right).

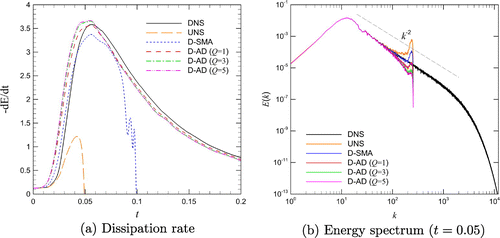
Figure 11. Time evolution of the energy spectrum for the Burgers turbulence problem based upon the ensemble average of 64 sample fields obtained by DNS ($N=32768$) (left), and energy spectra at time $t=0.05$ obtained by various spatial resolutions ranging from $N=512$ to $N=32768$ (right).

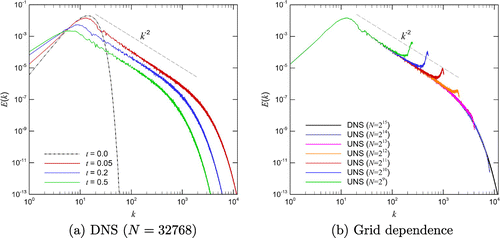
Figure 12. Results for the SGS modeling of the Burgers turbulence problem obtained using $N=512$ resolution with the skew-symmetric formulation of the nonlinear term: time evolution of the total dissipation rate (left) and energy spectra at time $t=0.05$ (right).

Figure 13. A sensitivity analysis with respect to the free filtering parameter $\alpha$ for solving the Burgers turbulence problem and showing the energy spectra at time $t=0.05$ using the conservative formulation on $N=512$ resolution.

Figure 14. A sensitivity analysis with respect to the free filtering parameter $\alpha$ for solving the Burgers turbulence problem and showing the energy spectra at time $t=0.05$ using the skew-symmetric formulation on $N=512$ resolution.