One-centre corrected two-electron integrals in inner projection-based integral evaluations

Abstract

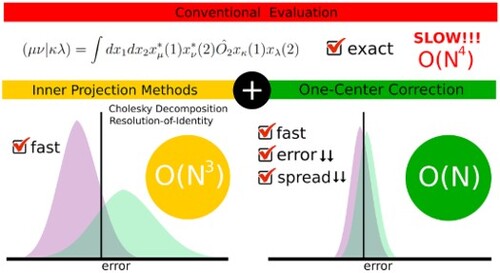
Cholesky decomposition (CD) of the two-electron integrals and the resolution-of-identity (RI) techniques are established inner projection methods to efficiently evaluate two-electron integrals. Both approaches share the notion of an auxiliary basis set as a mean to reduce the scaling. In the past years, the close relationship between the two approaches has fostered developments on how to systematically derive unbiased auxiliary basis sets – atomic CD (aCD) and atomic compact CD (acCD) auxiliary basis sets, different to the precomputed auxiliary basis sets. The accuracy of these approximations in the RI approach can be further improved via an explicit correction of the one-centred two-electron integrals, which is the main object of this research. Correcting the one-centred two-electron integrals directly, which scales linear with system size, is expected to provide a new degree of freedom to the design of auxiliary basis sets. This can either be used to gain faster convergence towards the conventional treatment of the two-electron integrals or as a mean to design lighter auxiliary basis sets while maintaining the same accuracy as of the uncorrected approach. The benchmarks of the one-centre corrections applied to several auxiliary basis set types were investigated in this paper.

GRAPHICAL ABSTRACT

Keywords:

• Coulomb integrals
• Cholesky decomposition
• resolution of identity
• density fitting
• two-electron integral approximations

1. Introduction

The optimal fundamentals of two-electron integral approximations – a three-centre approximation of the four-centre integrals in terms of an auxiliary basis set, the Resolution-of-Identity (RI) approach – were established by Vahtras et al. [2]. Although, similar approaches have been suggested in the past [3], Vahtras et al. determined that the expansion coefficients computed in the Coulomb metric were the most accurate approach. The resulting method yields a universal expression of the substitution of any types of two-electron integrals – one-, two-, three- and four-centre integrals – with a simplified expression, avoiding any explicit four-centre integrals. The major achievement of this approach was that the scaling of the computation of the two-electron integrals was reduced from formally $\mathcal{O}(N^4)$ to $\mathcal{O}(N^3)$, where N is the size of the valence basis set. While the report by Vahtras et al. established a unique procedure to compile the optimal expansion coefficients, the design of the expansion basis – later called the auxiliary basis set – was less detailed. Nevertheless, they stated that ‘… the expansion basis set should in principle include all one-centre products of the original basis set’ and further asserted that ‘… it is necessary to reproduce the behaviour of the exact expansion near the atomic nuclei’.

Over the last half century, various groups have proposed routes towards the optimal design of these auxiliary basis sets. A full review of this subject is beyond the scope of this report; however, it is worth to note that different approaches have been proposed. On one hand is the development of the precomputed auxiliary basis sets originally championed and developed by the Karlsruhe group [4,5]. On the other is the school that derives the auxiliary basis sets from the original product basis of the valence basis functions [6–8]. Recently, approaches intermediate to these methods were developed. Automatic generation of auxiliary basis functions via an expansion with preoptimised parameters was done in the cases of auto-ABS [9] and AutoAux [10]. This paper will not take issue on this matter. Rather, it will take issue on the obvious matter that the one-centre two-electron integrals are approximated in the RI approach. These integrals should be the most significant in introducing any error in describing the electron density close to the atomic nuclei. Hence, it is the goal of this investigation to demonstrate that a substantial part of the error in the total energy in the RI approximation can be removed if the one-centre two-electron integrals are not approximated. This investigation will demonstrate that the proposed correction at the HF and DFT level of approximation is trivial to implement and that the approach in general constitutes a significant improvement in accuracy regardless of the design of the RI auxiliary basis set.

This paper is subsequently structured as follows: first, a brief review of the RI approach is presented in the theory section. This will set the stage for the one-centre correction to be introduced. Second, the computational details will be presented. This is followed by results and discussion, and this paper is concluded with a brief summary.

2. Theory

The fundamentals of the RI approach are described as follows. Vahtras et al. made the ansatz in which the valence product basis is expressed as a linear combination of auxiliary functions, (1) ${\varphi }_{\mu }{\varphi }_{\nu }=\mu \nu =\sum _K{c}_{\mu \nu }^K{\theta }_K=\sum _K{c}_{\mu \nu }^{K}K$(1) where ${\varphi }_{\mu }$ and ${\varphi }_{\nu }$ are two valence basis functions, ${\theta }_K$ is an auxiliary basis function and $c_{\mu \nu }^K$ is an expansion coefficient. This is followed by a simplified notation. That is, the valence and auxiliary basis functions are just denoted by their index in geminal greek and capital latin characters, respectively. Vahtras et al. demonstrated that the optimal expansion coefficient was accessed by optimising the overlap between the product basis and the approximating linear combination of auxiliary functions in the Coulomb metric. Thus the expansion coefficients are optimised by minimising the self-interaction energy, ${ϵ}_{\mu \nu }$, which can be expressed in the chemist's notations as (2) ${ϵ}_{\mu \nu }=(\mu \nu -\sum _K{c}_{\mu \nu }^{K}K|\mu \nu -\sum _L{c}_{\mu \nu }^{L}L)$(2) Differentiating with respect to the expansion coefficients and setting the gradient to zero results in Equation (3(3) $(\mu \nu |K)=\sum _L{c}_{\mu \nu }^L(K|L)$(3) ) (3) $(\mu \nu |K)=\sum _L{c}_{\mu \nu }^L(K|L)$(3) Here, $(\mu \nu |K)$ and $(K|L)$ are the so-called three- and two-centre integrals, respectively. Finally, by multiplying both sides with the inverse of the two-centre integrals, the expansion coefficients are expressed as (4) $c_{\mu \nu }^L=\sum _K(\mu \nu |K)(K|L{)}^{-1}$(4) Hence, the two-electron integrals can be expressed as (5) $(\mu \nu |\kappa \lambda )=\sum _{KL}{c}_{\mu \nu }^K(K|L)c_{\kappa \lambda }^L=\sum _{KL}(\mu \nu |K)(K|L{)}^{-1}(L|\kappa \lambda )$(5) It is noted that the very same equations are derived if the error in general interaction integrals is minimised, that is, if (6) ${ϵ}_{\mu \nu ,\kappa \lambda }=(\mu \nu -\sum _K{c}_{\mu \nu }^{K}K|\kappa \lambda -\sum _L{c}_{\kappa \lambda }^{L}L)$(6) is the starting point for the derivation.

Following a Cholesky decomposition of the inverted two-centre integral matrix, $(K|L{)}^{-1}=(Z{Z}^T{)}_{K,L}$, the two-electron integrals are now conveniently expressed as (7) $(\mu \nu |\kappa \lambda )=\sum _K{R}_{\mu \nu }^K{R}_{\kappa \lambda }^K$(7) where $R_{\mu \nu }^K=\sum _L{c}_{\mu \nu }^L{Z}_L^K$ are either the so-called Cholesky vectors or the corresponding RI vectors depending on the choice of the auxiliary basis set.

In the SCF and the DFT methods, the two-electron integrals contribution to the Fock matrix, $F^{(2)}$, are expressed as (8) $F_{\mu \nu }^{(2)}=\sum _{\kappa \lambda }{D}_{\kappa \lambda }((\mu \nu |\kappa \lambda )-\frac{\alpha }{4}(\mu \kappa |\nu \lambda )-\frac{\alpha }{4}(\mu \lambda |\nu \kappa ))$(8) where $D_{\kappa \lambda }$ is the electronic one-particle density matrix expressed in the basis of the valence basis set and α is a parameter to set the fraction of exchange that is included. $\alpha =1$ and $\alpha =0$ correspond to HF and pure DFT calculations and intermediate values are found in hybrid DFT calculations. For computational efficiency, the actual two-electron integrals are never evaluated according to Equation (7(7) $(\mu \nu |\kappa \lambda )=\sum _K{R}_{\mu \nu }^K{R}_{\kappa \lambda }^K$(7) ). Rather, the expression is used to change the order of summations and to promote clever screenings. For example, the Coulomb contribution to the Fock matrix, $F^C$, is evaluated as (9) $F_{\mu \nu }^C=\sum _K{R}_{\mu \nu }^K{Y}^K$(9) where $Y^K=\sum _{\kappa \lambda }{R}_{\kappa \lambda }^K{D}_{\kappa \lambda }$ is a precontraction of the Cholesky or RI vectors with the one-particle density matrix. For the exchange contribution, the schemes are more complicated. The interested reader is, for example, suggested to look at the paper by Aquilante et al. [11] for the derivation and implementation of the so-called LK method.

In the current implementation in Openmolcas [12], the 1-centre correction (1CC) to the energy and Fock matrix is implemented by having a modified integral-direct SCF driver which only allows for the addition from exact 1-centre two-electron integrals $({\mu }_A{\nu }_A|{\kappa }_A{\lambda }_A)$, where the subscript on the basis function index denotes the centre A. This is followed by a second modified code which constructs the 1-centre two-electron integrals from the Cholesky or RI vectors, contracts them with the corresponding 1-particle density matrix and finally subtracts the contribution from the Fock matrix. These trivial modifications now render the two-electron integrals to be treated exactly for 1-centre integrals, while the 2-centre, 3-centre and 4-centre two-electron integrals are approximated by the use of the auxiliary basis functions. It is expected that this trivial correction will significantly reduce the acquired error due to the use of the standard Cholesky or RI method. The rest of this paper is devoted to demonstrate this effect.

The concept of using some exact integrals in a density fitting scheme is, however, not completely novel. Hollman et al. [13] used exact integrals for the integral classes $({\mu }_A{\nu }_A|{\kappa }_A{\lambda }_A)$ and $({\mu }_A{\nu }_B|{\kappa }_A{\lambda }_B)$ to cure the so-called robust concentric atomic density fitting (CADF) scheme from the collapse of the semi-positiveness of the two-electron integral tensor. This was tested in terms of the HF benchmark calculations using DZ to 5Z valence basis sets in connection with various precomputed auxiliary basis sets. In contrast, this study will explore the inclusion of the smaller subset of exact 1-centre two-electron integrals in the context of a standard molecular RI approach for HF and DFT methods. Moreover, the effect of this correction will be explored for both the precomputed auxiliary basis sets and the systematically CD derived counterpart.

3. Computational details

The main objective of this paper is to demonstrate that the exact 1-centre two-electron integrals corrections can achieve higher accuracy that is general to any inner projection integral evaluation scheme. To achieve this, a variety of CD and RI methods are spanned and contrasted with respect to accuracy to conventional computationally expensive exact calculation of two-electron integrals. Additionally, this work also addressed the dependence in RI auxiliary basis sets. This paper presents a compelling proof that the errors in the 1-centre two-electron integrals approximations in CD and RI schemes are highly significant and 1CC scheme can offer linear scaling correction independent of integral evaluation scheme, wave function description and auxiliary basis set size.

Initially, this work will address CD and RI methods with systematically derived auxiliary basis functions where they are derived from the initial valence basis set via Cholesky decomposition. Integral approximation schemes that belong to this category are the Full Cholesky Decomposition (FCD) [14], the 1-Centre Cholesky Decomposition (1C-CD) [7], and RICD with either atomic CD auxiliary basis (aCD) [7] or atomic compact CD auxiliary basis (acCD) [8]. In the latter part of this paper, the current 1CC scheme is applied to precalculated auxiliary basis sets, the RIJ and RIJK auxiliary basis sets [4,5,15]. The RIJ class of auxiliary basis set designed specifically to approximate Coulomb integrals, while the RIJK class is optimised to approximate both Coulomb and exchange integrals.

To evaluate the method accuracy the study evaluated three characteristics of the method errors – the change in the mean absolute error in the total energy, the maximum absolute error and the dispersion of the error distribution – as the 1-centre correction is applied. In this work, the error in total energy per molecule was calculated as (10) ${\epsilon }_i=\frac{E_i^{\mathrm{conv}}-E_i^{CD/RI}}{N_i^{\mathrm{electrons}}}$(10) where $E_i^{\mathrm{conv}}$ and $E_i^{CD/RI}$ are the conventional and CD/RI-based total ground state energies, respectively, and $N_i^{\mathrm{electrons}}$ is the number of electrons in the molecule i. The mean absolute error (MAE) was evaluated using (11) $\mu =\sum _i^N\frac{|{\epsilon }_i|}{N}$(11) while the maximum absolute error was determined as ${\epsilon }_{max}=max\{{\epsilon }_i:i=1,N\}$, and the sample standard deviation, σ, was calculated as (12) $\sigma =\sqrt{\frac{\sum _i^N({\epsilon }_i-\mu {)}^2}{N-1}}$(12) where N is the number of molecules in the sets used in this study (see below). These three numerical measures were used to gauge accuracy and approximation homogeneity in both classes of auxiliary basis sets.

Furthermore, this work employs two distinct molecular data bases of molecular structures as test suites to address molecular diversity. The first database is the G2/97 test set which includes open- and closed-shell systems [16]. After removing monoatomic entries, 73 molecules are left and served as test set I. The structures are given in the Supporting Information (SI). The second test suite is opted to test molecules with possibly higher angular momentum auxiliary functions [17]. In total, 24 molecules are included in Set II which are also available in the SI. To test its effect in relative energy, interaction or reaction energies for three chemical systems were also calculated and summarised in Table S4. Specifically, we considered atomisation of tetrahedral $P_4$ cluster, Diels–Alder reaction and formamide–formamide interaction. Corresponding structures are included in SI. Geometry optimisations of a pentameric water cluster were also done. The initial and optimised structures of the cluster are also available in SI.

3.1. Systematically derived auxiliary basis sets

The utility of the proposed 1CC scheme is initially studied in the context of systematically derived auxiliary basis sets. To evaluate the effect of correcting the 1-centre integrals, comparative analysis was done using FCD, 1C-CD, aCD, acCD and 1CC-acCD approaches as implemented in OpenMolcas quantum chemical software package. The two first approaches are included as references to compare against the corrected and non-corrected RI approaches. The valence basis set choice spans a variety of typical basis sets in computational chemistry.

Using molecular Set I, performance evaluations were done using HF- and DFT-based methods. DFT calculations were done using BLYP [18–20], a non-hybrid functional, and B3LYP [19–21], a hybrid functional. The calculations were done using the Pople's 6-31G** [22,23], Dunning's cc-pVXZ ($\mathrm{X}=\mathrm{D},\mathrm{Q}$) [24,25] and Widmark's ANO-L-VXZP ($\mathrm{X}=\mathrm{D},\mathrm{Q}$) [26,27]. The Cholesky decomposition threshold, τ, was set to ${10}^{-4}$. This τ value was previously determined to give an absolute error in the total energy within 0.01 kcal/(mol·electron) [28].

Set II is also subjected to HF, BLYP and B3LYP methods with 6-31G**, ANO-L-VDZP, ANO-L-VQZP, cc-pVDZ and cc-pVQZ. The decomposition parameter, τ, was also set to 10${}^{-4}$, similar to that of Set I.

To calculate relative energies, selected chemical systems are subjected to single point energy calculations using HF with ANO-L-VDZP basis set in combination with different 2-electron approximation schemes. Reaction energy ($E_{rxn}$) is calculated as (13) $E_{rxn}=E_P-E_R$(13) where $E_P$ and $E_R$ are the optimised product and reactant energies, respectively.

Another common relative energy calculation is the interaction energy determination of multi-molecular complex. The interaction energy ($I{E}_{AB}$) between molecules A and B can be calculated as (14) $I{E}_{AB}=E_{AB}-E_A^{AB}-E_B^{AB}$(14) where $E_{AB}$, $E_A^{AB}$ and $E_B^{AB}$ are the energies of AB complex, molecule A and B in AB complex geometry, respectively. Additionally, interaction energy was also corrected with respect to the basis set superposition error (BSSE). The BSSE corrected IE is calculated as (15) $I{E}_{AB}=E_{AB}-E_{A,AB}^{AB}-E_{B,AB}^{AB}$(15) where $E_{A,AB}^{AB}$ and $E_{B,AB}^{AB}$ are the energies of molecules A and B in AB complex geometry using AB complex basis, respectively.

To test the effect of the proposed correction to the course of optimisation and to the equilibrium structure, a pentameric water cluster was optimised using HF/6-31G** level of theory with different 2-electron integral approximations.

Other molecular properties which are often calculated are functions of the molecular orbital energies. This includes global reactivity parameters such ionisation potential and electron affinity as well as local reactivity parameters such as Fukui functions and other indices based on local electron density. Therefore, the effect of 2-electron integral approximation methods to molecular orbital energies were studied and as a representative property, HOMO–LUMO energy gap was chosen which can be calculated as (16) $E_{HOMO-LUMO}=E_{LUMO}-E_{HOMO}$(16) This property does not only describe reactivity of the system but can also be used to approximate excitation energy in electronic transition which is related to charge transport and optical properties of the system.

3.2. Precalculated auxiliary basis sets

Sampling both classes of auxiliary basis is imperative to prove the general applicability of the proposed 1CC scheme to any RI based approximations. Here, the focus is shifted to the precalculated auxiliary basis sets, RIJ and RIJK [4,5,15]. However, it is expected that the results obtained are generalisable to other RIJ and RIJK auxiliary basis sets which are guided by similar design principles. The effect of 1CC to RIJ and RIJK auxiliary basis function based calculations was also studied using the first data base. This test includes RIJ, 1CC-RIJ, acCD and 1CC-acCD using the BLYP density functional and RIJK, 1CC-RIJK, acCD and 1CC-acCD employing either BLYP or B3LYP levels of theory. This utilised Ahlrichs's basis sets, def-SVP and def-TZVP [29,30]. It should be noted that these RIJ and RIJK auxiliary basis functions were originally optimised using these valence basis sets.

4. Results and discussion

The theory laid out earlier discusses the fundamentals of the CD and RI approximations, which were previously demonstrated to be both an expression of an inner projection approach to approximate the two-electron integrals [2]. As proposed earlier, exact computation of 1-centred two-electron integrals could dramatically increase the accuracy of all CD and RI-based schemes. However, the improvement of CD and RI-based approximation methods generally rely on the quality of the associated auxiliary basis sets. Hence, below the results will be discussed separately depending on the design of the auxiliary basis sets – systematically derived or precomputed.

4.1. Systematically derived auxiliary basis sets

The results of single point calculations to ascertain the impact of the 1CC scheme on RI-based schemes are included in this section. To initiate the discourse, mean absolute errors for the molecules of Set I were summarised in Figure 1. It can be seen that the 1C-CD MAE is generally the largest followed by the FCD approach. This is expected as 1C-CD employs a one-centre approximation where only atom-centred products are used over the Cholesky decomposition approach, while the FCD also uses 2-centre auxiliary functions. RICD, on the other hand, uses the RI formalism with CD derived 1-centre auxiliary basis sets, aCD and acCD. The acCD basis set is obtained through the removal of linear dependence of the primitives Gaussians via subsequent CD applied to the aCD auxiliary basis set. These methods were found to have comparable mean errors at CD threshold τ equal to 10${}^{-4}$. An earlier work showed that the accuracy of aCD and acCD is equivalent at such threshold [28]. Comparing both families of systematically derived auxiliary basis sets, it is also emphasised that RICD achieved lower MAE than the CD-based approaches which were also stated in previous studies – using the same threshold yields a larger auxiliary basis for the aCD/acCD approach as compared to FCD/1C-CD.

Figure 1. Mean absolute total energy errors in μHa for Set I calculated with different valence basis set (6-31G**, ANO-L-VDZP, ANO-L-VQZP, cc-pVDZ and cc-pVQZ) in combination with various CD/RI-based integral evaluations (FCD, 1C-CD, aCD, acCD and 1CC-acCD) using (A) HF, (B) BLYP and (C) B3LYP levels of theory.

Upon applying 1CC to the acCD auxiliary basis, a significant decrease in the calculated MAE was found. The improvement in accuracy holds true for all three ab-initio models investigated in this study, supporting the significance of the 1-centre corrections. In general, the magnitude of decrease in MAE, as a consequence of 1CC, is inversely proportional to valence basis set size. In systematically derived one-centre auxiliary basis sets, the auxiliary basis functions are inner projections of the original atomic product valence basis function and hence, their sizes are quadratically related. Smaller valence basis consequently leads to proportionally smaller auxiliary basis, which in turn leads to inferior integral approximations. In this regard, the exact correction of one-centre two-electron integral has greater effect on the accuracy of the theoretical model. This is particularly evident when using the 6-31G** as valence basis set. In the HF case, a decrease of 7.21 μHa is observed. On the other end of the spectrum, larger basis sets benefits little to none with the proposed correction. In a large auxiliary basis, more one-centre products are used and included the approximation of the one-centre two-electron integrals approaches the exact value. Therefore, the correction, in absolute terms, has minimal contribution in increasing the associated accuracy. This is highlighted when using ANO-L-VQZP which is the largest basis set in this work which has a 0.116 μHa decrease in MAE. It should be noted that the calculated MAE is equal to 0.016 and 0.132 μHa with and without correction, respectively and hence 1CC-acCD still afforded an order of magnitude more accurate than the uncorrected. Corresponding results were observed for molecules in Set II as can be seen in Figure S1.

The spreads of the errors associated with acCD and 1CC-acCD using HF, BLYP and B3LYP for Set I are illustrated in Figure 2. For the interested reader, complete error distributions including FCD, 1C-CD and aCD for Sets I and II given for the three levels of theory are given in Figures S2–S7. It can be noted that all approximation methods suffer positive errors for HF and negative errors for BLYP. The B3LYP then has an intermediate error in comparison. This can be explained by the nature of the B3LYP functional which includes an HF exchange component with the original BLYP functional.

Figure 2. Box plot of signed total energy error distribution in μHa calculated using (A) HF, (B) BLYP and (C) B3LYP with different valence basis sets (6-31G**, ANO-L-VDZP, ANO-L-VQZP, cc-pVDZ and cc-pVQZ) for Set I. The two-electron integrals are calculated using the acCD and 1CC-acCD evaluation schemes. Boxes range from the 25th to 75th percentile of each signed error distribution. Vertical lines inside each box indicate median values while horizontally extended lines indicate nearby lying values in the first and fourth quartiles. Dots represent signed errors outside the 1.5 interquartile range. Note that different axis limits were used to aid visualisations.

After exactly correcting the $({\mu }_A{\nu }_A|{\kappa }_A{\lambda }_A)$ type integrals, it can be seen that the spread of error distribution decreased for any of the three ab-initio models studied here. In agreement to Figure 1, this is more pronounced when using the smaller auxiliary basis sets. Taking the same theoretical model as above, HF/6-31G**, the acCD and 1CC-acCD have ${\epsilon }_{max}$ of 40.651 and 8.302 μHa, respectively. The calculated σ also decreased from 10.532 to 1.594 μHa. Both parameters were found to decrease by an order of magnitude from the uncorrected scheme and corresponds to 79.58% and 84.87% decrease in ${\epsilon }_{max}$ and σ, respectively. The maximum absolute errors and standard deviations when using HF, BLYP and B3LYP are given in SI as Tables S1 and S2 for Sets I and II, respectively. To put this into perspective, a highly homogeneous error distribution would equate that the quality of integral approximation is the same for the span of molecular structures sampled here. This is essential in comparing energies of different molecules such as the reactants and products in computational mechanistic studies.

To further explore this, reaction energies for the atomisation of tetrahedral P4 cluster, Diels-Alder reaction of ethene and cis-butadiene and formamide–formamide interaction were investigated. In general, 1CC-acCD achieved the highest accuracy in agreement to the trends in the total energy errors. However, the magnitude of the error relative to the conventional evaluation is within a Joule per mole. Arguably, the achieved accuracy in relative energy in contrast to that of total energy is a result of cancellation of errors as evidenced by the above data. I. The effect of basis set superposition error proves to be minimal in the case of formamide dimer interaction energy calculation using HF and 6-31G** basis set. The average error per electron and BSSE-corrected formamide dimer interaction energy are summarised as Tables S4 and S5 in the SI, respectively. The optimisation of a pentameric water cluster also resulted to the same conformation regardless of the chosen integral approximation. However, molecular orbital energies differ significantly with the chosen integral approximation method and were highlighted in the HOMO–LUMO energy gap calculation. Calculated HOMO–LUMO energy gap for different approximation methods using different level of theory is given in Table 1. It can be seen that 1CC-acCD afforded the closest approximation to the conventional with 2.73 kJ$/$mol${}^{-1}$. The increase in the accuracy of 1CC-acCD from acCD by 2.18 kJ$/$mol${}^{-1}$ is attributed to the addition of the one-centre correction. Other properties such as electron distribution and repulsion as well as excited state chemistry and spectroscopy which rely on the determination of two-electron integrals are expected to benefit in a similar fashion. Additionally, post-HF methods such as MP2 are expected to better benefit from the correction as a consequence of the closer molecular orbital description than other approximation methods.

Table 1. Calculated HOMO–LUMO energy gap in Ha and kJ$/$mol${}^{-1}$ for the optimised pentameric water cluster using HF with 6-31G** basis set. $\mathrm{\Delta }E$ is the difference with conventional 2-e${}^{-}$ integral evaluation.

	$E_{HOMO-LUMO}$	$\mathrm{\Delta }E$
Approximation method	Ha	Ha	kJ mol^−1
Conventional	6.8056E-01	0.00	0.00
FCD	6.8226E-01	1.70E-03	4.46
1C-CD	6.8262E-01	2.06E-03	5.41
aCD	6.8242E-01	1.86E-03	4.88
acCD	6.8243E-01	1.87E-03	4.91
1CC-acCD	6.8160E-01	1.04E-03	2.73

The number of associated vectors used in the evaluations is another key factor in CD- and RI-based estimates. This directly affects the speed of integral evaluations. As the number of vectors scales with system size specifically the number of valence basis functions, it is convenient to do comparisons as the ratio of CD and RI vectors per valence basis functions. Figure 3 shows the calculated signed total energy errors as a function of number of CD and RI vectors per valence basis functions for 6-31G** and the Widmark's basis sets, ANO-L-VDZP and ANO-L-VQZP. The vector analysis when using Dunning's basis sets, cc-pVDZ and cc-pVQZ, is appended in Figure S8 and a corresponding figure for Set II is given as Figure S in the SI. The average number of CD and RI vectors per valence basis function in this section is summarised as Table S3 in the SI. The 1C-CD has lower number of associated vectors than the FCD as expected. Non-atom centred basis function products are removed in the set of auxiliary basis functions in 1C-CD which decreases the number of CD vectors.

Figure 3. Signed total energy errors in μHa as a function of the number of CD/RI vectors calculated using (A) HF, (B) BLYP and (C) B3LYP levels of theory. The two-electron integrals are determined using CD/RI-based evaluation schemes (FCD, 1C-CD, aCD, acCD and 1CC-acCD) in combination with different valence basis sets (6-31G**, ANO-L-VDZP and ANO-L-VQZP).

When using the Pople's 6-31G** basis set, the RI associated vector per valence basis function is smaller than that of CD methods. Interestingly, the performance of FCD and 1C-CD is poorer than RICD-based approximations despite having higher number of CD vectors. The number of RI vectors exceeded that of CD when a larger basis set is used. Naturally, the 1CC-acCD scheme also uses the same number of RI vectors with acCD. The one-centre contribution from the original approximation method is removed via the contraction with one-centre density matrix using the same set of RI vectors. After which the one-centre two-electron integral is calculated conventionally and added to the former. This can be seen in Figure 3 as a vertical shift towards zero when comparing acCD and 1CC-acCD.

4.2. Precomputed auxiliary basis sets

Up to this point, all auxiliary basis sets discussed are considered to be systematically derived. To prove that the 1CC scheme is general to all RI-based approximations, it is imperative to apply the same correction to precomputed auxiliary basis sets as well. An example of a precomputed auxiliary basis set is the RIJ auxiliary basis functions which was optimised to approximate Coulomb integrals. In this study, the particular RIJ auxiliary basis set used was optimised in association with Ahlrichs's basis sets, def-SVP and def-TZVP. This limited the choice of valence basis set to these.

The MAE for RIJ and acCD, without and with the 1CC correction, using molecular set I is summarised in Figure 4. acCD was found to be more accurate than the RIJ for both valence basis sets by more than 10 $\mu Ha$. Analogous to Figure 1, the current correction scheme, 1CC, effectively decreases MAE of both RIJ and acCD schemes with RIJ benefiting more than the acCD scheme in absolute terms. Using def-SVP, 1CC-RIJ and 1CC-acCD has a performance gain of 5.175 and 2.508 μHa, respectively. In the case of def-TZVP, comparable accuracy increase of 5.648 and 2.650 μHa is observed.

Figure 4. Mean absolute total energy errors in μHa for Set I calculated with different valence basis sets (def-SVP and def-TZVP) in combination with various RI auxiliary basis sets (RIJ, 1CC-RIJ, acCD and 1CC-acCD) using BLYP functional.

The signed error distribution for RIJ, 1CC-RIJ, acCD and 1CC-acCD is given in Figure 5 and the maximum absolute error, standard deviation and average number of RI vectors per valence basis function are given as Table S6 in the SI. Calculated maximum errors are found to decrease for both methods. For the acCD case, the 1CC scheme increases the homogeneity of the approximation. In contrast, though the MAE of RIJ decreased when using the exact correction, the spread of the error distribution remains highly similar with the uncorrected. This is further evidenced by the calculated standard deviations. Using def-TZVP, RIJ and 1CC-RIJ has σ equal to 6.870 and 6.803 μHa, respectively. This is equivalent to only a 0.98% decrease in σ. In comparison to that of acCD and 1CC-acCD, which decreased from 2.471 to 0.284 μHa, an 88.51% reduction in σ. As discussed earlier, the homogeneity of the approximation errors is important when comparing energies of different structures, typical to any reaction simulation. An inconsistent approximation error introduces uncertainty in calculated relative energies such as activation and reaction energies.

Figure 5. Box plot of signed total energy error distribution in μHa calculated using BLYP with different valence basis set (def-SVP and def-TZVP) for Set I. The two-electron integrals are calculated using RI-based evaluation schemes (RIJ, 1CC-RIJ, acCD and 1CC-acCD). Boxes range from the 25th to 75th percentile of each signed error distribution. Vertical lines inside each box indicate median values while horizontally extended lines indicate nearby lying values in the first and fourth quartiles. Dots represent signed errors outside the 1.5 interquartile range.

In the procedure reported by Eichkorn et al. [4], they described a three parameter optimisation via a Monte Carlo approach with a convergence criterion of $\mathrm{\Delta }J$ = 0.2 mHa per atom. As the method is focused on the total Coulomb energy, rather than individual Coulomb integrals, the procedure may have suffered from error cancellations during the optimisations. This causes the 1CC scheme which corrects the one-centred two-electron integrals to simply shift the distribution as no equivalent integrals are there to correct.

The relation of RI vectors and total energy errors is summarised in Figure 6. Parallel to 1CC-acCD having the identical number of RI vectors, 1CC-RIJ shares the same number of RI vectors with RIJ. Using def-TZVP basis, acCD has 2.54 more vectors per valence basis in comparison with RIJ which is a reasonable trade-off for a more accurate integral evaluation. In the 1CC-acCD scheme, this trade-off becomes more cost-effective with 17.228 $\mu Ha$ increase in accuracy than that of RIJ.

Figure 6. Signed total energy errors in μHa as function of the number of RI vectors calculated using BLYP with different valence basis sets (def-SVP and def-TZVP) for Set I. The two-electron integrals are determined using CD/RI-based evaluation schemes (RIJ, 1CC-RIJ, acCD and 1CC-acCD).

To further explore precomputed auxiliary basis sets, RIJK approximation was also studied. In Figure 7, RIJK and 1CC-RIJK can be compared with acCD and 1CC-acCD with respect to calculated MAE when using both BLYP and B3LYP functionals with def-SVP basis set. RIJK is optimised for both Coulomb and exchange components and it is normally used for hybrid DFT functional such as B3LYP. This explains the poorer approximations when using BLYP which is a non-hybrid functional.

Figure 7. Mean absolute total energy errors in μHa for Set I calculated with def-SVP valence basis set in combination with various RI auxiliary basis sets (RIJK, 1CC-RIJK, acCD and 1CC-acCD) using B3LYP and BLYP functionals.

Akin to all the previous cases, correcting the one-centred two-electron integrals decreased the corresponding MAE. The MAE of RIJ and acCD in combination with B3LYP decreased from 1.034 to 0.484 μH, and from 2.192 to 0.473 μHa, respectively. Using B3LYP functional, 1CC decreased the maximum absolute error of RIJK from 4.270 to 3.338 μHa while that of acCD from 7.345 to 2.424 μHa. This can be explained by the different number of vectors used in the RIJK approximation as compared to the acCD. The number of RI vectors per valence basis function is summarised as Figure 8 for the RIJK and acCD comparisons. It can be seen that RIJK auxiliary basis set is larger than RIJ and acCD. On average, RIJK has 2.964 more RI vectors per valence basis function greater than RIJ and 0.651 more in comparison with acCD. Even with a larger auxiliary basis, the MAE of 1CC-RIJK is greater than that of 1CC-acCD showing the advantageous position of a systematically derived auxiliary basis sets over the precomputed auxiliary basis sets when 1-centre two-electron integrals are corrected.

Figure 8. Signed total energy errors in μHa as function of the number of RI vectors calculated using B3LYP and BLYP functionals with def-SVP basis set for Set I. The two-electron integrals are determined using CD/RI-based evaluation schemes (RIJK, 1CC-RIJK, acCD and 1CC-acCD).

The error distributions for RIJK, acCD, 1CC-RIJK and 1CC-acCD are given in Figure 9 while the maximum absolute error, standard deviation and average number of RI vectors per valence basis function are given as Table S7 in the SI. Parallel to RIJ, the error distribution of RIJK was only shifted with 1CC with only 0.307 and 0.179 μHa decrease in the standard deviation for B3LYP and BLYP, respectively. This corresponds to 31.91% and 23.93% decrease in the calculated σ. This small distribution shift when correcting one-centred two-electron integrals is a manifestation of error cancellations during the design of the auxiliary basis as the current proposed scheme calculates exactly the one-centre integral and should, in theory, decrease the spread of the approximation. The acCD, however, afforded a decrease of 1.259 and 1.677 μHa in the standard deviation which is equivalent to 65.61% and 73.55% reduction, respectively. Again, this shows that 1CC in combination with acCD significantly increases the homogeneity of the integral approximation.

Figure 9. Box plot of signed total energy error distribution in μHa calculated using different DFT functionals (BLYP and B3LYP) with def-SVP valence basis set for Set I. The two-electron integrals are calculated using RI-based evaluation schemes (RIJK, 1CC-RIJK, acCD and 1CC-acCD). Boxes range from the 25th to 75th percentile of each signed error distribution. Vertical lines inside each box indicate median values while horizontally extended lines indicate nearby lying values in the first and fourth quartiles. Dots represent signed errors outside the 1.5 interquartile range.

Though not completely eliminating the negative eigenvalues in the density matrix, they found a factor of 2–5 decrease in error using different precomputed auxiliary basis sets relative to standard density fitting (DF) which is the same as RI. The increase in accuracy is expected as they included significantly greater number of exact two electron integrals increasing the associated computational effort. The number of $({\mu }_A{\nu }_B|{\kappa }_A{\lambda }_B)$ integral scales linear to the number of pair of centres or quadratic to the number of centres without any screening protocol.

After surveying different RI-based integral approximation procedures, it is evident that the proposed correction can decrease MAE in all RI methods. For systematically derived auxiliary basis sets, distribution analyses show that 1CC improves the uniformity of evaluations without increasing the number of associated vectors. This correction only adds a constant small linear scaling overhead per SCF calculation. It is important to note that the number of one-centre two-electron integrals scales linearly with the system size and hence, the 1CC is a linear scaling correction scheme. The 1CC terms can be evaluated and stored at the beginning of an SCF calculation. With the increase in accuracy and virtually inexpensive calculation, especially in small systematically derived auxiliary basis set, it highly recommended to employ one-centre correction scheme for any RI-based integral evaluations. On the other side of the coin, this work also implies that a smaller auxiliary basis can be designed together with the suggested correction and achieve an accuracy that of larger auxiliary basis. This in turn opens an avenue for faster approximation of the two-electron integral which composes the bulk of any SCF calculations.

5. Summary

The effect of exact correction for one-centred two-electron integrals to the accuracy of RI based evaluation schemes has been investigated for various ab-initio models. The molecular databases used provided a repertoire of open and closed shell structures with elements spanning the first three rows of the periodic table. The total electronic energy served as the primary metric for accuracy evaluation relative to the conventional direct evaluation of two centred integrals. Employing the 1CC approach lowered the mean absolute errors of all RI-based methods which reveals that the one-centred two-electron integrals constitute significant errors from these families of integral approximations. It should be noted that the performance gain depends on the design of auxiliary basis set. For systemically derived auxiliary basis which includes the spectrum of CD-based schemes, such as aCD and acCD, the increase in accuracy and decrease in range is inversely related to the auxiliary basis set size. In particular, one can observe reduction of the MAE, dispersion of the error distribution and the maximum absolute error which are close to 1 order of magnitude. For the precomputed auxiliary basis sets such as RIJ and RIJK schemes, the increase in accuracy is not dependent on the auxiliary basis set size and the range remained the same. Here, a smaller reduction of the MAE and the maximum absolute error are observed, however, this is not accompanied by a similar reduction of the dispersion of the error distribution, as observed for the systematically derived auxiliary basis functions. This shows that the associated accuracy of the precomputed auxiliary basis set may have benefited from significant error cancellations. The number of associated CD/RI vectors remains unchanged when correcting for the $({\mu }_A{\nu }_A|{\kappa }_A{\lambda }_A)$ type integrals. Calculating selected relative energies showed that 1CC achieved highest accuracy albeit the difference is only in Joules. Optimisation from same pentameric water cluster also converged to a single conformation independent of the approximation method. However, molecular orbital energies differ significantly with the chosen integral approximation method which is highlighted in the HOMO–LUMO energy gap with 1CC-acCD being the most accurate. This is expected to be beneficial to excited state description and computational spectroscopy. Additionally, post-HF methods such as MP2 would also benefit with the high fidelity description of molecular orbitals. In practice, the one-centre correction would scale linear to the size of the system and such integral evaluation can be done once at the start of SCF calculations which renders the correction virtually free of charge with a significant increase in accuracy. Finally, in the context of the seCADF approach of Hollman et al., using exact two-electron integrals for all 1-centre integrals and one of the three 2-centre integrals classes, provided an accuracy improvement of a factor of 2–5 in comparison with standard molecular RI using precomputed auxiliary basis functions. The current implementation indicates that this type of accuracy improvement or better can be experienced with a much more trivial and limited correction to the standard molecular RI approach, especially in connection with systematically derived CD style auxiliary basis sets.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Correction Statement

This article has been corrected with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

The Swedish Research Council (VR, Grant No. 2020-03182) and Stiftelsen Olle Engkvist Byggare (SOEB, Grant No. 211-0019) are acknowledged for funding. The computations were enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) at the National Supercomputing Centre funded by the Swedish Research Council through grant agreement no. 2022-06725.