Relative energies of increasingly large [n]helicenes by means of high-level quantum chemical methods

Abstract

We investigate the relative stability of increasingly large helicenes at the CCSD(T) level via the high-level G4(MP2) thermochemical protocol. The relative energies of [n]helicenes (n = 4–9) are obtained via the following reaction: [n]helicene + benzene → [n + 1]helicene + ethene. This reaction conserves the number of sp²-hybridized carbons, the number of aromatic rings, and the helical structures on the two sides of the reaction. We show that the reaction energy converges to an asymptotic value of ΔH₂₉₈ =  + 22.4 kJ/mol for increasingly large helicenes. For comparison, for [n]acenes, the same reaction converges to a much higher asymptotic reaction enthalpy of ΔH₂₉₈ =  + 56.8 kJ/mol. This difference between the two asymptotic reaction enthalpies sheds light on the relative thermodynamic stability of increasingly large helicenes. We proceed to use the G4(MP2) reaction energies to evaluate the performance of dispersion-corrected density functional theory (DFT) and semiempirical molecular orbital (SMO) methods for the relative energies of [n]helicenes. Nearly all DFT methods perform poorly with root-mean-square deviations (RMSDs) above 10 kJ/mol. The best-performing DFT method, BLYP-D4, attains an RMSD = 5.2 kJ/mol. Surprisingly, the advanced SMO methods, XTB and PM7, outperform the DFT methods and result in RMSDs of 3.0 and 3.1 kJ/mol, respectively.

GRAPHICAL ABSTRACT

KEYWORDS:

• CCSD(T)
• G4(MP2)
• helicenes
• polycyclic aromatic hydrocarbons

1. Introduction

Helicenes are ortho-fused polycyclic aromatic hydrocarbons (PAHs) that adopt a chiral 3D topology due to their spatial helical arrangement. Helicenes have attracted significant interest due to their unique catalytic, nanochemical, optical and electronic properties [1–7]. The smallest helicene, and the first one to be synthesised, is [4]helicene (a.k.a. benzo[c]phenanthrene). Small helicenes (e.g. [4] and [5]helicene) exhibit a flip-flop chirality inversion that can be catalysed by nanographene flakes and cyclophanes [8–11]. The activation energy for the enantiomerization of larger helicenes have been measured to be 100.8 ([5]helicene), 148.1 ([6]helicene), 172.4 ([7]helicene), 175.3 ([8]helicene) and 180.3 ([9]helicene) kJ mol^–1 [12]. Thus, larger helicenes exist as highly stable axial enantiomers and have found applications in asymmetric synthesis and catalysis.

The largest [n]helicene that has been synthesised includes 16 ortho-fused benzene rings ([16]helicene) [13,14]. Expanded helicenes (i.e. helicenes composed of alternating linear and ortho-fused rings) [15] of up to [23]helicene have been synthesised [16]. For comparison, linear acenes with only up to 7 benzene rings (heptacene) have been isolated in bulk [17], and the largest metastable linear acene that has been investigated experimentally includes 12 benzene rings (dodecacene) [18–20]. Thus, despite both helicenes and linear acenes being catacondensed PAHs, large helicenes are synthetically more accessible. Indeed, [n]acenes become more reactive with an increasing number of rings [21].

Thus, a natural question that arises is how does the energetic stability of increasingly larger helicenes increase with the size of the system? Here, we address this question at the CCSD(T) level. In particular, we use the high-level G4(MP2) composite ab initio method to investigate the relative energetic stability of increasingly larger [n]helicenes (n = 4–9) via the following reaction: (1) $\begin{array}{r}[n]\text{helicene }+\text{ benzene}\to [n+1]\text{helicene }+\text{ ethene}\end{array}$(1)

This reaction provides a systematic approach for comparing the energetic stability of increasingly larger [n]helicenes. The high-level G4(MP2) calculations are not feasible for helicenes larger than [9]helicene (C₃₈H₂₂) with the computational resources available to us. Therefore, in order to investigate the relative stabilities of larger [n]helicenes, we benchmark the performance of prominent density functional theory (DFT) methods relative to the G4(MP2) reference values for [n]helicenes (n = 4–9). We then use the best-performing DFT method (BLYP-D4) to investigate the relative stability of [n]helicenes up to n = 36. We show that the same trends observed for the smaller [n]helicenes using the G4(MP2) method persist for larger [n]helicenes.

DFT methods are routinely used for investigating the relative stability and other energetic properties of [n]helicenes and their derivatives (for representative examples, see references [8–11,22–35]). However, the performance of DFT methods for calculating the relative stability of helicenes has not been systematically studied. Here, we use the above G4(MP2) reaction energies to evaluate the performance of a representative set of dispersion-corrected DFT methods from rungs 1–4 of Jacob’s Ladder. We find that nearly all of the DFT methods tend to systematically overestimate the relative stabilities of the helicenes and result in relatively poor performance with overall root-mean-square deviations (RMSDs) exceeding 10 kJ mol^–1.

2. Computational details

High-level ab initio calculations with the composite ab initio G4(MP2) thermochemical protocol [36,37] were performed to obtain reaction energies. The G4(MP2) protocol is a computationally efficient composite ab initio procedure for obtaining highly accurate thermochemical properties for organic systems at the CCSD(T) level (coupled cluster with singles, doubles and quasiperturbative triple excitations) [38,39]. Even for total atomisation energies, which are amongst the most challenging thermochemical properties for quantum chemical methods, deviations between the CCSD(T) and full configuration interaction (FCI) method are typically bellow ∼4 kJ mol^–1 at the complete basis-set (CBS) limit [40,41]. G4(MP2) theory has been found to produce gas-phase thermochemical properties (such as reaction energies, bond dissociation energies and enthalpies of formation) with a mean absolute deviation (MAD) of 4.3 kJ mol^–1 from the experimental energies of the G3/05 test set [36]. In addition, G4(MP2) theory has been found to produce accurate theoretical thermochemical properties with MADs below the threshold of chemical accuracy (i.e. 4.2 kJ mol^–1), including hydrocarbon atomisation, isomerisation and conformational energies [42–47]. The geometries for the G4(MP2) calculations (i.e. for [n]helicene and [n]acene, n = 3–9) have been obtained at the B3LYP-D3BJ/def2-TZVP level of theory [48–52]. It should be noted that the B3LYP-D3BJ functional has been found to provide excellent performance for calculating equilibrium structures of organic molecules [53]. Harmonic vibrational frequency analyses have been performed at the same level of theory to confirm that all stationary points are equilibrium structures (i.e. they have all real vibrational frequencies). The zero-point vibrational energy, enthalpic and entropic corrections have been obtained from such calculations.

We have also optimised the geometries for a set of larger [n]helicenes (n = 4–36) at the B3LYP-D3BJ/def2-SVP level of theory. The B3LYP-D3BJ/def2-SVP reference geometries are only employed for the calculation of the approximate BLYP-D4/def2-TZVPP reaction energies reported in Table S1 (vide infra). Apart from that, all the G4(MP2), DFT and semiempirical molecular orbital (SMO) calculations employ the B3LYP-D3BJ/def2-TZVP geometries.

We use the benchmark G4(MP2) reaction energies as reference values to evaluate the performance of a representative set of DFT methods from rungs 1–4 of Jacob’s Ladder [54]. The DFT functionals that are considered in the present study are listed in Table 1. The DFT single-point energy calculations were performed in conjunction with the large Def2-QZVPP basis set [50]. We use two types of dispersion corrections, namely, the recently developed D4 empirical dispersion correction [55,56] (or its predecessor, the D3BJ dispersion correction) [51,52] and the Vydrov–van Voorhis (VV10) nonlocal dispersion correction [57]. Methods from the fifth rung of Jacob’s Ladder, i.e. double-hybrid DFT (DHDFT) methods, are not considered in the present work since their steep computational cost makes them inapplicable to large PAHs. In addition, it is not clear that the G4(MP2) reference values are sufficiently accurate for evaluating the performance of DHDFT methods [58,59]. We also consider the performance of a number of semiempirical molecular orbital methods listed in Table 1.

Table 1. Density functional theory (DFT) exchange-correlation functionals and semiempirical molecular orbital (SMO) methods considered in the present work.

Method	Jacob’s Ladder Rung^a	Methods
DFT	LDA	SVWN [60]
	GGA	BLYP [48,61], PBE [62]
	MGGA	TPSS [63], M06-L [64], MN15-L [65], B97M-V [66], r^2SCAN [67]
	HGGA	B3LYP [48,49], PBE0 [68], BH&HLYP [69]
	HMGGA	TPSSh [70], PW6B95 [71], M06 [72], M06-2X [72], MN15 [65]
	RS	CAM-B3LYP [73], ωB97X [74], ωB97X-D [75], ωB97M-V [66]
SMO	N/A	AM1 [76], PM6 [77], PM7 [78], XTB [79,80]

^aLDA = local density approximation, GGA = generalised gradient approximation, MGGA = meta-GGA, HGGA = hybrid-GGA, HMGGA = hybrid-meta-GGA, RS = range-separated.

All geometry optimisations, frequency calculationsand DFT calculations were performed using the Gaussian 16 programme suite [81]. The CCSD(T) calculations involved in the G4(MP2) protocol were performed with the Molpro 2016 programme [82]. XTB refers to the GFN2-xTB version, and these calculations were performed with Grimme’s XTB code (version 6.5.1) [79,80].

3. Results and discussion

3.1. Non-dynamical correlation effects in increasingly large [n]helicenes

Before examining the G4(MP2) CCSD(T) relative energies, it is of interest to examine non-dynamical correlation effects in [n]helicenes of increasing sizes. Table 2 gathers a number of coupled cluster-based diagnostics for quantifying the importance of non-dynamical correlation effects, namely the %TAE[(T)] [40,42,83], ${\mathcal{T}}_1$ [84] and D₁ diagnostics [85–87]. The ${\mathcal{T}}_1$ diagnostic of Lee and Taylor is the Euclidean norm of the vector of the CCSD t₁ amplitudes divided by the square root of the number of correlated electrons. It has been suggested that ${\mathcal{T}}_1$ values below 0.02 indicate systems that are not dominated by a multireference character [84,88]. In a similar manner, the D₁ diagnostic is defined as the matrix 2-norm of the CCSD t₁ amplitudes, and it has been suggested that D₁ values below 0.05 indicate systems for which the CCSD (or CCSD(T)) method is applicable. In contrast, the %TAE[(T)] diagnostic is an energy-based coupled cluster diagnostic which is defined as the percentage of the CCSD(T) total atomisation energy (TAE) accounted for by the quasiperturbative triple excitations (T), namely %TAE[(T)] = 100 × (TAE[CCSD(T)]–TAE[CCSD])/TAE[CCSD(T)], where TAE[CCSD] and TAE[CCSD(T)] are the TAEs calculated using the CCSD and CCSD(T) methods, respectively. Extensive benchmarking against post-CCSD(T) contributions suggests that %TAE[(T)] values below 5% indicate systems characterised by mild-to-moderate nondynamical correlation effects [40,42,83].

Table 2. Overview of coupled cluster-based diagnostics for nondynamical correlation for [n]helicenes (n = 4–9)^a.

Compound	${\mathcal{T}}_1$	D1	%TAE[SCF]	%TAE[(T)]
Benzene	0.0108	0.0294	81.5	1.46
Naphthalene	0.0111	0.0326	80.9	1.66
Phenanthrene	0.0112	0.0324	80.6	1.75
[4]helicene	0.0113	0.0323	80.3	1.82
[5]helicene	0.0113	0.0328	80.1	1.87
[6]helicene	0.0113	0.0321	79.9	1.90
[7]helicene	0.0113	0.0322	79.8	1.94
[8]helicene	0.0113	0.0321	79.6	1.97
[9]helicene	0.0113	0.0319	79.5	1.99

^aAll the diagnostics are taken from the CCSD(T)/6-31G(d) calculations involved in the G4(MP2) composite ab initio calculations.

The diagnostics in Table 2 indicate that the [n]helicenes considered in the present work (n = 4–9) are dominated by dynamical correlation and that post-CCSD(T) contributions are expected to be relatively modest. For the sake of completeness, results are also provided for the smaller PAHs: benzene, naphthalene, anthracene and phenanthrene. The ${\mathcal{T}}_1$ diagnostics spread over a fairly narrow range from 0.0108 (benzene) to 0.0113 ([n]helicene, n = 4–9) and are below the recommended cutoff value of 0.02, indicating no significant multireference character. The D₁ diagnostics spread over a wider range from 0.0294 (benzene) to 0.0328 ([5]helicene). However, they are also below the recommended cutoff value of 0.05. Moving on to the energy-based %TAE[(T)] diagnostics, the %TAE[(T)] values range from 1.46% (benzene) to 1.99% ([9]helicene). These values indicate that post-CCSD(T) contributions are expected to be relatively small for the [n]helicenes considered in the present work. We also consider the %TAE[SCF] diagnostic [83], which is the percentage of the TAE accounted for at the Hartree–Fock level relative to the TAE at the CCSD(T) level. The %TAE[SCF] values range from 81.5 (benzene) to 79.5% ([9]acene) and demonstrate that ∼80% of the CCSD(T) TAE is accounted for at the Hartree–Fock level. Importantly, all of the coupled-cluster-based diagnostics (${\mathcal{T}}_1$, D₁, %TAE[(T)] and %TAE[SCF]) remain relatively constant for the [n]helicenes (n = 4–9). We note in this context that Mazziotti and co-workers have shown, based on natural orbital occupation numbers, that [n]acenes develop greater polyradical character as the number of rings increases relative to arch-shaped PAHs [89].

3.2. G4(MP2) relative energies of increasingly large [n]helicenes

For helicenes, including up to nine benzenoid rings (i.e. C₃₈H₂₂), we were able to calculate the electronic energies at the CCSD(T) level by means of the G4(MP2) composite ab initio method using B3LYP-D3BJ/def2-TZVP reference geometries. These [n]helicene structures are shown in Figure 1. We note that the CCSD(T)/6-31G(d) calculation for [9]helicene ran for 10 days on 16 cores of 2.4 GHz Intel Xeon Gold 6230 node with 1024 GB of RAM. We begin by examining the reaction energies of reaction (1) for increasingly large [n]helicenes. Table 3 gives the G4(MP2) reaction energies on the electronic (ΔE_e), enthalpic at 0 K (ΔH₀), enthalpic at 298 K (ΔH₂₉₈) and Gibbs-free at 298 K (ΔG₂₉₈) potential energy surfaces. In the following discussion, we will focus on the enthalpic reaction energies at 298 K. However, the same trends are observed on the electronic (ΔE_e) and Gibbs-free (ΔG₂₉₈) potential energy surfaces.

Figure 1. Top and side views of the B3LYP-D3BJ/def2-TZVP optimised geometries for the [n]helicene (n = 4–9). Atomic colour scheme: H, white; C, grey.

Table 3. G4(MP2) reaction energies for reaction (1) on the electronic (ΔE_e), enthalpic at 0 K (ΔH₀), enthalpic at 298 K (ΔH₂₉₈) and Gibbs-free at 298 K (ΔG₂₉₈) potential energy surfaces (in kJ mol^–1). The [n]helicene structures are shown in Figure 1.

Reaction^a	ΔEe	ΔH0	ΔH298	ΔG298
phenanthrene + benzene → [4]helicene + ethene	52.3	46.9	49.9	52.7
[4]helicene + benzene → [5]helicene + ethene	43.5	36.1	39.5	40.1
[5]helicene + benzene → [6]helicene + ethene	34.0	26.8	30.2	32.4
[6]helicene + benzene → [7]helicene + ethene	30.2	23.2	26.5	30.1
[7]helicene + benzene → [8]helicene + ethene	25.7	18.7	21.9	27.8
[8]helicene + benzene → [9]helicene + ethene	26.0	19.1	22.4	24.7

^aNote that these reactions conserve the number of sp²-hybridized carbons and number of aromatic rings on the two sides of the reaction and also conserve similar helicene structures on the two sides of the reaction, namely [n]helicene and [n+1]helicene (see text).

Reaction (1) provides means for estimating the energy of adding another benzenoid ring to form [n + 1]helicene from [n]helicene. Importantly, this reaction conserves large molecular fragments on both sides of the reaction, and therefore systematic errors associated with deficiencies in the CCSD(T) reaction energies are expected to partly cancel out between the reactants and products [44,45,47,90–99]. In particular, reaction (1) conserves both the number of aromatic rings and the number of sp²-hybridized carbons on the two sides of the reaction. We note that there are other possible reactions that conserve the number of aromatic rings and the number of sp²-hybridized carbons on the two sides of the reaction. For example, reaction (2) from reference 100, which is also numbered reaction (2) in the present work: (2) $[n]\text{helicene }+(n\text{--}1)\text{ ethene }\to n\text{benzene}$(2)

Nevertheless, this reaction involves a decreasing degree of error cancellation between reactants and products as the size of the [n]helicene increases. For example, for the largest helicene for which we were able to calculate the G4(MP2) energy, the left side of this reaction involves [9]helicene, whereas the right side of the reaction involves 9 isolated benzene molecules. In contrast, reaction (1) is generally applicable to any helicene size since it involves [n]helicene on one side of the reaction and [n + 1]helicene on the other side. Thus, the chemical environments on the two sides of the reaction become increasingly more similar as the size of the [n]helicene increases. For example, [8]helicene and [9]helicene should involve similar chemical structures and energetic properties. An elegant illustration of this is provided by considering a reaction similar to reaction (16) in reference 101, namely the transformation of two [n]helicenes into [n–1]helicene and [n + 1]helicene, via the following reaction: (3) $\begin{array}{r}2\times [n]\text{helicene }\to [n\text{--}1]\text{helicene }+[n+1]\text{helicene}\end{array}$(3)

The G4(MP2) reaction enthalpies at 298 K for this transformation are –10.5 (n = 4), –9.3 (n = 5), –3.7 (n = 6), –4.5 (n = 7), + 0.4 (n = 8) kJ mol^–1. Therefore, as expected, the reaction enthalpy converges to zero with the size of the helicene. The reason for this can be intuitively understood by contemplating the scenario where n approaches infinity.

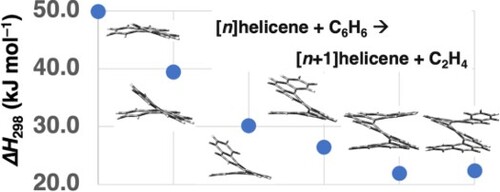
Let us proceed with examining the G4(MP2) reaction enthalpies for reaction (1). Transforming phenanthrene to [4]helicene via reaction (1) is an endothermic process with a reaction energy of ΔH₂₉₈ = 49.9 kJ mol^–1. This relatively high reaction enthalpy could be partly attributed to the larger aromatic stabilisation energy associated with the left-hand side of the reaction [100]. Transforming [4]helicene to [5]helicene via the same process results in a lower reaction energy of ΔH₂₉₈ = 39.5 kJ mol^–1. That is, the reaction becomes less endothermic by ∼10 kJ mol^–1. Similarly, transforming [5]helicene to [6]helicene further reduces the endothermicity of the reaction by another ∼10 kJ mol^–1 with a reaction enthalpy of ΔH₂₉₈ = 30.2 kJ mol^–1. For the transformation of [6]helicene to [7]helicene, we obtain a reaction energy of ΔH₂₉₈ = 26.5 kJ mol^–1, and for the next transformation of [7]helicene to [8]helicene, we obtain a reaction energy of ΔH₂₉₈ = 21.9 kJ mol^–1. Therefore, it is evident that the reaction energy is converging to a constant value as the two sides of the reactions become more and more similar. Accordingly, the transformation of [8]helicene to [9]helicene, is associated with a reaction energy of ΔH₂₉₈ = 22.4 kJ mol^–1. The convergence of the reaction energy of reaction (1) is illustrated in Figure 2.

Figure 2. G4(MP2) ΔH₂₉₈ reaction enthalpies for reaction (1) ([n]helicene + benzene → [n+1]helicene + ethene, blue circles) and reaction (4) ([n]acene + benzene → [n+1]acene + ethene, orange circles) (in kJ mol^–1). The reaction enthalpies are taken from Tables 3 and 4.

In the second part of the manuscript, we use the G4(MP2) benchmark reaction energies to assess the performance of a range of DFT procedures. We find that the GGA method BLYP-D4 is the best-performing DFT method and, somewhat surprisingly, outperforms the functionals from rungs 3 and 4 of Jacob’s Ladder. Prior to examining the results of the benchmark DFT study, it is of interest to use the best-performing DFT method (BLYP-D4) to see if the energy of reaction (1) converges to a constant value for helicenes larger than [9]helicene. We have examined helicenes up to [36]helicene (C₁₄₆H₇₆). Table S1 of the Supporting Information lists the BLYP-D4/def2-TZVPP reaction energies. These results show that, as expected, the reaction energy is converging to a constant value. For example, for reactions involving helicenes larger than [17]helicene, the reaction energy generally changes by ≤ 0.1 kJ mol^–1 between each consecutive reaction.

The above results show that increasing the length of large helicenes by consecutive addition of benzene rings (via reaction (1)) is an endothermic process with an asymptotic reaction energy of ΔH₂₉₈ = ∼22 kJ mol^–1. It is of interest to compare this asymptotic reaction energy to that obtained for linear acenes: (4) $[n]\text{acene }+\text{ benzene }\to [n+1]\text{acene }+\text{ ethene}$(4)

Reaction (4) is the equivalent reaction (1) for [n]acenes. Similar to reaction (1), reaction (4) conserves both the number of sp²-hybridized carbons and the number of aromatic rings on the two sides of the reaction, as well as the similarly sized acenes on the two sides of the reaction. Therefore, even though acenes are expected to involve a higher degree of multireference character than helicenes (vide supra), reaction (4) benefits from a certain degree of systematic error cancellation between reactants and products. Table 4 lists the G4(MP2) reaction energies for reaction (4) for [n]acenes (n = 3–9). Converting [3]acene (anthracene) into [4]acene via reaction (4) is an endothermic process associated with a reaction enthalpy of ΔH₂₉₈ = 51.8 kJ mol^–1. As expected, this reaction enthalpy is similar to that of converting phenanthrene into [4]helicene via reaction (1) (ΔH₂₉₈ = 49.9 kJ mol^–1, Figure 2 and Table 3). The endothermicity of the reaction increases by 3.0 kJ mol^–1 when moving to the conversion of [4]acene to [5]acene (Table 4). For the consecutive conversion of larger acenes, the reaction enthalpy converges rapidly to a value of ΔH₂₉₈ = 56.8 kJ mol^–1. The reaction enthalpy converges to this asymptotic value for the conversion of [6]acene to [7]acene and does change for larger acenes (Table 4 and Figure 2).

Table 4. G4(MP2) reaction energies for reaction (4) on the electronic (ΔE_e), enthalpic at 0 K (ΔH₀), enthalpic at 298 K (ΔH₂₉₈) and Gibbs-free at 298 K (ΔG₂₉₈) potential energy surfaces (in kJ mol^–1)^a.

Reaction^a	ΔEe	ΔH0	ΔH298	ΔG298
[3]acene + benzene → [4]acene + ethene	55.8	48.3	51.8	52.9
[4]acene + benzene → [5]acene + ethene	58.9	51.2	54.8	55.8
[5]acene + benzene → [6]acene + ethene	60.5	52.7	56.3	57.3
[6]acene + benzene → [7]acene + ethene	61.0	53.0	56.7	57.7
[7]acene + benzene → [8]acene + ethene	61.2	53.2	56.8	57.9
[8]acene + benzene → [9]acene + ethene	61.2	53.2	56.8	57.8

^aNote that these reactions conserve the number of sp²-hybridized carbons and number of aromatic rings on the two sides of the reaction, and also conserve similar acene structures on the two sides of the reaction, namely [n]acene and [n+1]acene (see text).

Therefore, whereas the increase in size for helicenes via reaction (1) is associated with an asymptotic reaction enthalpy of ΔH₂₉₈ = 22.4 kJ mol^–1 for each consecutive step, the increase in size for acenes via reaction (4) is associated with a much higher asymptotic reaction enthalpy of ΔH₂₉₈ = 56.8 kJ mol^–1 for each consecutive step. This difference between the two asymptotic reaction enthalpies may partly explain why large helicenes of up to [16]helicene and expanded helicenes of up to [23]helicene have been synthesised [13–16]. The less endothermic asymptotic limit obtained for [n]helicenes relative to [n]acenes may be attributed to the larger aromatic stabilisation energy associated with branched PAHs relative to linear PAHs [101,102]. In addition, intramolecular π-π interactions between the superimposed benzene rings in the higher members of the [n]helicenes series may also contribute to the difference between the two asymptotic limits [103]. Since such intramolecular π-π interactions exist for helicenes larger than [6]helicene, they may also account for the slower convergence rate observed for the helicenes in Figure 2.

3.3. Performance of DFT and SMO methods for the relative energies of increasingly large [n]helicenes

We now turn to the performance of a representative set of DFT methods to predict the relative stabilities of increasingly large helicenes as described by reaction (1). We consider DFT methods from rungs 1–4 of Jacob’s Ladder, as well as SMO methods (see Table 1). Table 5 gives an overview of the performance of the DFT methods considered in this work. Inspection of Table 5 reveals that the relative stability of increasingly large helicenes is an exceptionally challenging problem for practically all DFT methods. We start by noting that, with no exception, DFT methods systematically overestimate the energy of reaction (1), as demonstrated by MAD = MSD across the board. We also note that (i) the inclusion of a dispersion correction significantly improves the performance of functionals that were not parameterised to reproduce dispersion interactions, and (ii) the more recent D4 dispersion correction generally performs better than its predecessor D3BJ.

Table 5. Performance of DFT and SMO methods for the energy of reaction (1) relative to CCSD(T) isomerisation energies obtained from G4(MP2) theory (in kJ mol^–1)^a.

Type^b	Functional	Dispersion^c	RMSD	MAD	MSD
LDA	SVWN	N/A	20.5	19.7	19.7
GGA	PBE	D3BJ	15.9	15.4	15.4
	PBE	D4	12.9	12.5	12.5
	BLYP	D3BJ	8.3	8.2	8.2
	BLYP	D4	5.2	5.1	5.1
MGGA	M11-L	N/A	23.1	22.8	22.8
	M06-L	N/A	23.0	22.8	22.8
	M06-L	D4	17.9	17.8	17.8
	r^2SCAN	D4	17.7	17.4	17.4
	B97M-V	VV10	16.6	16.4	16.4
	MN15-L	N/A	14.9	14.8	14.8
	TPSS	D3BJ	12.7	12.5	12.5
	TPSS	D4	9.4	9.2	9.2
HGGA	PBE0	D3BJ	18.0	17.8	17.8
	BH&HLYP	D4	17.2	17.1	17.1
	PBE0	D4	16.0	15.8	15.8
	HF^d	D4	15.8	15.7	15.7
	B3LYP	D3BJ	13.8	13.6	13.6
	B3LYP	D4	10.9	10.9	10.9
	B3PW91	D3BJ	9.2	9.1	9.1
HMGGA	M06	N/A	22.9	22.5	22.5
	M06-2X	N/A	22.4	22.1	22.1
	M06-HF	N/A	20.5	20.1	20.1
	MN15	N/A	19.3	19.2	19.2
	PW6B95	D4	18.3	18.0	18.0
	PW6B95	D3BJ	17.8	17.7	17.7
	M06	D4	15.4	15.2	15.2
	TPSSh	D4	10.9	10.8	10.8
	B1B95	D4	9.7	9.6	9.6
	BMK	D3BJ	8.2	8.0	8.0
RS	ωB97X	D4	25.7	25.4	25.4
	ωB97	D4	23.7	23.4	23.4
	ωB97X-D	N/A	20.5	20.4	20.4
	ωB97M-V	VV10	17.8	17.7	17.7
	CAM-B3LYP	D3BJ	19.6	19.4	19.4
	CAM-B3LYP	D4	17.4	17.2	17.2
SMO	AM1	N/A	46.3	44.1	44.1
	PM3	N/A	34.1	31.7	31.7
	PM6	N/A	13.4	10.7	10.3
	PM7	N/A	3.1	2.1	–2.1
	XTB	N/A	3.0	2.7	1.5

^aMAD = mean absolute deviation, MSD = mean signed deviation, RMSD = root mean square deviation. ^bLDA = local density approximation, GGA = generalised gradient approximation, MGGA = meta-GGA, HGGA = hybrid-GGA, HMGGA = hybrid-meta-GGA, RS = range separated, SMO = semiempirical molecular orbital. ^cN/A indicates dispersion is included in the functional form or is not applicable. ^dHartree–Fock method is listed for comparison.

Let us begin with a key finding that the generalised gradient approximation (GGA) method BLYP-D4 outperforms all the functionals from rungs three and four of Jacob’s Ladder, and results in an RMSD of merely 5.2 kJ mol^–1. PBE-D4, on the other hand, performs poorly with an RMSD of nearly three times as large (namely, RMSD = 12.9 kJ mol^–1). The best-performing meta-GGA (MGGA) functional, TPSS-D4, results in an RMSD of nearly twice as large (namely, RMSD = 9.4 kJ mol^–1). It is important to note that the reference reaction energies vary between 26.0 and 52.3 kJ mol^–1 (Table 3), therefore RMSDs on the order of ∼10 kJ mol^–1 represent very high percentage errors. With the exception of BLYP-D4, BLYP-D3BJ and TPSS-D4, all the considered GGA and MGAA functionals result in RMSDs > 10 kJ mol^–1.

The best-performing global hybrid GGAs, B3PW91-D3BJ and B3LYP-D4, still result in high RMSDs of 9.2 and 10.9 kJ mol^–1, respectively. Similarly, the best-performing hybrid-meta GGA methods, BMK-D3BJ and B1B95-D4, result in RMSDs of 8.2 and 9.7 kJ mol^–1, respectively. Thus, overall, DFT methods from rung four of Jacob’s Ladder do not offer an improvement over methods from rungs two and three. The range-separated hybrid DFT methods show particularly poor performance, with RMSDs ranging between 17.4 (CAM-B3LYP-D4) and 25.7 (ωB97X-D4) kJ mol^–1.

As noted above, all the DFT functionals systematically overestimate the reaction energy of reaction (1), as evident from MAD = MSD. These highly systematic errors suggest that linear scaling of the reaction energies would significantly improve the performance of the DFT methods. It is important to note that our intention is not to scale the reaction energies as a practical approach for improving the performance of DFT methods, but simply to demonstrate the extent to which a single scaling factor can lower the RMSDs. Table S2 of the supporting information gives an overview of the performance of the scaled DFT-D4 methods, in which the reaction energies are scaled by a single empirical scaling factor (α), which has been optimised to minimise the RMSDs. Not surprisingly, scaling is a highly effective approach for reducing the systematic error associated with the DFT methods. The RMSDs in Table 5 are reduced by 63–81% upon scaling. For example, the RMSD for B1B95-D4 is reduced from 9.7 to 1.8 kJ mol^–1 upon scaling the reaction energies by a factor of α = 0.7931. For comparison, a method that is already performing well without scaling, such as BLYP-D4, requires a scaling factor closer to unity. Namely, the RMSD for BLYP-D4 is reduced from 5.2 to 1.8 kJ mol^–1 upon scaling the reaction energies by a factor of α = 0.8829.

Let us move on to the performance of the SMO methods. Perhaps the most surprising result of this benchmark study is that the more recent SMO methods, PM7 and XTB, result in an excellent performance with RMSDs of 3.1 and 3.0 kJ mol^–1, respectively. These two methods are not biased toward systematic overestimation of the reaction energies, as demonstrated by the MAD and MSD values in Table 5. The good performance of these methods is also demonstrated by the fact that scaling the PM7 and XTB reaction energies by an optimal empirical scaling factor (α) does not significantly improve their performance. Upon scaling, the RMSD for PM7 is reduced from 3.1 to 2.3 kJ mol^–1, and the RMSD for XTB is reduced from 3.0 to 2.7 kJ mol^–1. We note that the optimal scaling factors for both methods are close to unity. Namely, we obtain a scaling factor of α = 1.0582 for PM7 (which tends to underestimate the reaction energies) and α = 0.9689 for XTB (which tends to overestimate the reaction energies) (Table 5). Thus, PM7 and XTB, which are computationally much more economical than DFT methods, outperform all of the considered DFT methods. This surprising result is attributed to the severe and systematic tendency of the DFT methods to overestimate the reaction energies. Indeed, the only methods in Table 5 for which this systematic overestimation is not observed are PM7 and XTB. This indicates that the more advanced SMO methods are able to attain a more balanced performance compared to DFT. We note, however, that scaling the DFT energies by a single empirical scaling factor results in better performance compared to the SMO methods. In particular, RMSDs as low as 1.8 kJ mol^–1 are attained for the BLYP-D4 and B1B95-D4 methods (vide supra). Finally, we note that older-generation SMO methods AM1, PM3 and PM6 result in poor performance with RMSDs of 46.3, 34.1 and 13.4 kJ mol^–1, respectively.

4. Conclusions

We obtain accurate relative energies of increasingly large [n]helicenes (n = 4–9) at the CCSD(T) level by means of the G4(MP2) thermochemical protocol. The relative energies are obtained via the reaction [n]helicene + benzene → [n + 1]helicene + ethene. This reaction conserves the number of sp²-hybridized carbons and the number of aromatic rings on the two sides of the reaction. In addition, for the larger helicenes, this reaction also conserves similar helical structures on the two sides of the reaction. We show that the reaction energy converges to an asymptotic value of ΔH₂₉₈ = 22.4 kJ mol^–1 at the G4(MP2) level, which does not significantly change for larger helicenes. For comparison, for [n]acenes, the same reaction converges to a much higher asymptotic reaction enthalpy of ΔH₂₉₈ = 56.8 kJ mol^–1. This difference between the two asymptotic reaction enthalpies sheds light on the relative thermodynamic stability of increasingly large helicenes and is consistent with the larger aromatic stabilisation energy associated with branched PAHs relative to linear PAHs. In addition, intramolecular π-π interactions between the superimposed benzene rings in the higher members of the [n]helicenes series may also contribute to the difference between the two asymptotic limits and the slower convergence rate observed for the helicenes relative to the acenes in Figure 2.

High-level composite ab initio methods such as G4(MP2) are computationally too prohibitive for calculating the relative energies of large helicenes. Therefore, density functional theory (DFT) methods are routinely used for investigating the energetic properties of [n]helicenes and their derivatives. However, the performance of DFT for the relative stability of increasingly larger helicenes has not been evaluated in a systematic manner. Here, we use our high-level G4(MP2) reaction energies to evaluate the performance of dispersion-corrected DFT methods from rungs 1–4 of Jacob’s Ladder as well as semiempirical molecular orbital (SMO) methods for the relative energies of [n]helicenes. Nearly all the considered DFT methods result in poor performance with root-mean-square deviations above 10 kJ mol^–1. The GGA method BLYP-D4 emerges as the best DFT method with an RMSD of 5.2 kJ mol^–1 and outperforms the functionals from rungs 3 and 4 of Jacob’s Ladder. Surprisingly, advanced semiempirical methods, namely XTB and PM7, outperform the DFT methods and result in RMSDs of 3.0 and 3.1 kJ mol^–1, respectively.

Acknowledgments

This work is dedicated to the lifetime achievements and memory of Professor Tim Lee and in honour of Professor Lee’s numerous scientific contributions to the fields of quantum chemistry, spectroscopy and astrochemistry. We gratefully acknowledge the generous allocation of computing time from the National Computational Infrastructure (NCI) National Facility, and system administration support provided by the Faculty of Science Agriculture Business and Law to the Linux cluster of the Karton group.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by National Computational Infrastructure: [Grant Number dv9].