Diversified role of fuzzified particle concentration on Casson gold-blood nanofluid flow through an elongating sheet for different shape nanoparticles

Abstract

The theme of this work is to explore the impact of shape factor on magnetized Casson gold-blood nanofluid flow through elongated sheet using fuzzified volume fraction. The impact of Ohmic heating, convective heating and suction/injection on heat transfer rate, is incorporated. The existing ordinary differential equations (ODEs) are transformed into fuzzy differential equations by applying the α-cut technique of fuzzy numbers. The α-cut value ranges from 0 to 1, which determines the level of fuzziness in the TFNs. The results indicate that rise in the Casson parameter leads to a reduction in the boundary layer thickness and an augmentation of shear stress near the sheet. Additionally, among the nanoparticle shapes studied, cylindrical nanoparticles demonstrate the extreme thermal conductivity, followed by platelet and blade-shaped nanoparticles, all contributing to an improvement in the heat transfer rate. The present code is validated numerically with previous works and found in good agreement.

KEYWORDS:

• Casson nanofluid
• non-uniform heat sink/source
• stretching sheet
• convective heating
• fuzzy volume fraction
• fuzzy differential equations

Nomenclature

$(A^{\ast },B^{\ast })$	=	Non-uniform heat source/sink parameters
$B$	=	Magnetic field$(T)$
$\mathrm{Bi}$	=	Biot number
$c$	=	Stretching rate $(s^{-1})$
$C_P$	=	Heat capacity $(J/(\text{kg}\text{.}\text{K}))$
$\overline{E}$	=	Electric field $(N/C)$
$\mathrm{Ec}$	=	Eckert number
$F$	=	Non-dimensional velocity
$J$	=	Current density
$\mathrm{Mn}$	=	Magnetic field parameter
$P_z$	=	Yield stress of the fluid
$\mathrm{Pr}$	=	Prandtl number
$\tilde{q}$	=	Heat flux$(W/m^2)$
$R{e}_x$	=	Local Reynolds number
$S$	=	Suction parameter
$t$	=	Time $(s)$
$T$	=	Temperature $(K)$
$U$	=	Free stream velocity $(m/s)$
$V_w$	=	Velocity of suction/injection$(m/s)$
$x,y$	=	Rectangular coordinates $(m)$

Greek symbols

$\beta$	=	Casson parameter
$\mathrm{\Theta }$	=	Non-dimensional temperature
$\kappa$	=	Thermal conductivity $(W/(\text{m}\text{.K}))$
${\lambda }_i,i\le 5$	=	Constants
$\mu$	=	Dynamic viscosity $(\text{kg}/(\text{m}\text{.s}))$
$\xi$	=	Similarity variable
$\rho$	=	Density $(\text{kg}/{\text{m}}^{\text{3}})$
$\sigma$	=	Electrical conductivity $(\mathrm{\Omega }\text{.m}{)}^{-1}$
${\tau }_o$	=	Relaxation time for heat flux$(s)$
$\tau$	=	Thermal relaxation parameter
$\varphi$	=	Nanoparticles volume fraction
$\psi$	=	Stream function

Subscripts

$\mathrm{Au}$	=	Gold nanoparticle
$\mathrm{Blood}$	=	Base fluid (blood)
$\mathrm{nf}$	=	Nanofluid
$s$	=	Surface
$\mathrm{\infty }$	=	Ambient condition

Superscripts

$\ast$	=	Asterisk
${}^{\mathrm{\prime }}$	=	Derivative with respect to $\eta$

Abbreviations

CC	=	Cattaneo–Christov
DEs	=	Differential equations
FDEs	=	Fuzzy differential equations
LNN	=	Local Nusselt number
PDEs	=	Partial differential equations
RKF	=	Runge–Kutta–Fehlberg
SFC	=	Skin friction coefficient

1. Introduction

In science and engineering, heat transfer flow is crucial, as it involves complex physical properties like chemical diffusion, magnetic effects and heat transfer are described by linear or nonlinear differential equations (DEs). However, these equations are affected by uncertainties such as mechanical defects, experimental errors and measurement errors, which make it challenging to obtain accurate solutions using traditional methods. The FST (Fuzzy Sets Theory) provides an accurate approach to dealing with such uncertainties, allowing us to model physical problems with unknown variables and IBCs (Initial and Boundary Conditions) using FDEs. The FST was first announced by Zadeh [1] and subsequently developed by Dubois and Prade [2], who introduced arithmetic procedures for fuzzy numbers (FNs). The FNs are variables with values ranging from 0 to 1, with each value assigned a membership grade indicating its degree of certainty. The use of FDEs has become increasingly popular in the recent years, with research focusing on fuzzy differentiability and integration. The idea of fuzzy differentiability was introduced by Seikala [3] and Kaleva [4], in which they incorporated the definition of fuzzy differentiation as well as integration. Buckley et al. [5] developed two methods for solving them: the modified principle and fuzzy numbers. Nieto [6] explored the Cauchy problem for continuous FDEs. Overall, FST and FDEs offer a suitable tool for modelling dynamical systems together with uncertainty. Lakshmikantham and Mohapatra [7] explored IVP for fuzzy differential equations, while Park and Han [8] applied the consecutive approximation tactic to determine the existence and uniqueness of solutions for FDEs. Gasilov et al. [9] investigated the systems of FDEs with triangular fuzzy numbers. FDEs have found numerous applications across different areas of science and engineering due to their ability to handle ambiguous and uncertain environments. The use of FDEs in various areas is mentioned by the authors [10–12]. More recently, FDEs with α-cut approaches have been employed to investigate heat flow problems in fuzzy environments, as demonstrated by [13–17].

The novel class of heat transfer fluid, i.e. “Nanofluid” was introduced in 1995 by Choi [18] and is prepared by suspending nano-sized particle whose diameter is less than 100 nm into base fluid, i.e. H₂O, C₂H₆O₂, kerosene oil, etc. It is widely used in various technology areas like solar energy [19], biomedical applications [20], heat exchangers [21], cooling in nuclear reactors [22], refrigeration system of electronics devices [23]. The thermal analysis of Casson–Au multiphase fluid flow through steep channel was displayed by Hussain et al. [24]. Nazeer et al. [25] have discussed the effect of Au and Ag solid particles on multiphase flow of viscous fluids flow via steep channel. The third-grade fluid flow through a channel under the impact of electroosmotic force was discussed by Choudhari et al. [26]. Irfan et al. [27] examined the impact of Casson nanofluid on peristaltic flow through channel with slip conditions. The scrutiny of heat transfer performance of Sutterby nanofluid flow with Darcy–Forchheimer medium was evaluated by Khan et al. [28]. Ellahi et al. [29] have observed the heat transfer performance of nanofluid flow inside truncated wavy cone. Similarly, the impact of various nanoparticles on viscous flows is explained in the literature [30–36].

The shape of nanoparticles has significant influence on nanofluid thermophysical properties, due to which the heat transfer enhancement occurs. There are various experimental and numerical studies that allocated with the shape consequence of nanoparticles. Jeong et al. [37] deliberated experimentally ZnO shape consequence of nanoparticles on thermophysical properties of (ZnO–H₂O) and revealed that viscosity of ZnO–H₂O augmented with rise in the volume concentration up to 69%. Moreover, the augmentation in viscosity of the rectangular shape nanoparticles is achieved to be bigger by 7.7%, than spherical shape of nanoparticles. Elias et al. [38] examined the impact of various shape factors of nanoparticles, i.e. Boehmite alumina nanoparticle on γ-AlOOH-H₂O/ethylene glycol nanofluid using entropy generation. Various shapes of the existing nanoparticles are considered. They reported that entropy generation and heat transfer rate (HTR) for nanofluids holding cylindrical shape is advanced in comparison with other shapes of nanoparticles. Ellahi et al. [39] found an analytical result for shape factor scrutiny of magnetic nanofluid flow over a permeable cone with natural convection, entropy generation and radiation effects. The influence on thermophysical properties of TiO₂–Cu/H₂O due to various shapes (cylindrical, bricks and platelet) in 2D flow over stretching surface with magnetic field is inspected by Ghadikolaei et al. [40]. A numerical study based on magnetized SiO₂–H₂O nanofluid and MoS₂−SiO₂/H₂O flow over a curved geometry under the impression of radiation and shape factor is presented by Iqbal et al. [41]. They examined that blade-shaped nanoparticles of MoS₂−SiO₂/H₂O have supreme temperature and brick-shaped nanoparticles of SiO₂–H₂O have lowest temperature. The influence of shape factor on Al₂O₃–Cu/H₂O flow in crosswise and streamwise direction is investigated by Ramesh [42]. They found that the HTR of platelet shape is greater than cylinder shape and the HTR of cylinder shape is greater than brick shape. Vanaki et al. [43] have considered the nanoparticle shape impact on various nanofluid flows through wavy channel with several phase shift, and noted that the SiO₂–ethylene glycol with platelets nanoparticle shape offers maximum HT augmentation as compared to rest of the tested nanofluids. Maraj et al. [44] studied the shape factor of MoS₂−SiO₂/H₂O inside porous cone and investigated that supreme temperature is obtained for blade shape nanoparticle of SiO₂/H₂O nanofluid whereas deepest temperature is noted in the brick shape nanoparticle of MoS₂–SiO₂/H₂O hybrid nanofluid. Moreover, the particle shape factor analysis on various nanofluids/hybrid nanofluid is examined in [45–48].

The literature cited above served as inspiration for the current work, which theoretically examines the impact of various nanoparticle shapes on the MHD flow of Au-blood nanofluid over a sheet. The sheet's surface is subjected to suction and convection heating. Along with Ohmic heating, a non-uniform heat source is also assisting the heat transfer mechanism which is modelled using C–C HFM (Cattaneo-Christov Heat Flux Model).

On the following grounds, this work's sole motivation is questioned:

1. How does the fluid behaviour vary with variation in magnetic field, Casson factor, Biot number and thermal relaxation parameter for both suction and injection.

2. What effect does nanoparticles shape have on fluid velocity and temperature? Among the considered shapes, which of them leads to superior heat transfer performance.

3. Examining the effect of the nanoparticle volume percent on the velocity and temperature outlines while treating it as a fuzzy number

In the current work, throughout the computation, the Prandtl number of blood is 24. The flow equations are in PDEs form and an approximate solution for the same is obtained by reducing them into simpler form, i.e. ODEs and then applying numerical method, i.e. Runge–Kutta fourth-order technique combined with shooting. To authenticate the correctness of the applied methodology, the obtained outcomes are validated with previous published works.

2. Formulation of problem

2.1. Problem assumptions and modelling

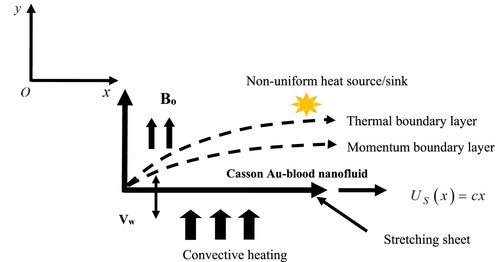
Contemplate a 2D flow of Casson nanofluid over a sheet subject to linear stretching is addressed. The sheet is stretching along x-axis with velocity $U_s(=\mathrm{cx})$ and free stream velocity of flow is $U\to 0$and flow restricted to $y>0$ (see Figure 1). The working fluid is a Casson nanofluid which is prepared by dispering gold (Au) nanoparticles in blood (Casson fluid); the properties of solid particle (gold) and base fluid (blood) are stated in Table 1. A magnetic field of uniform strength $B_o$ is exerted normal to the stretching surface which produces magnetic effects. Further, it is assumed that the fluid is weakly electrical conducting and as a result the impact of induced magnetic field is insignificant.

Figure 1. Schematic flow diagram.

Table 1. Blood and gold physical properties [49].

Properties	Blood	Gold
$\mu$ (kg/ms)	0.003–0.004	–
$\rho$ (kg/m^3)	1053	19300
$C_p$ (J/kgK)	3594	129.1
$\kappa$ (W/mK)	0.492	318
$\sigma$ (Ωm)^−1	0.8	4.10*10^7

The energy expression is modelled using C–C HFM [50,51] and energy transfer is supported by the heating due to the existence of magnetic field, i.e. Ohmic heating together with non-uniform heat source. Also, the surface of the geometry is showing to the consequence of suction with convective heating.

2.2. Casson fluid model

The Casson fluid expression is written as [52] (1) ${\tau }_{\mathrm{ij}}=\{\begin{array}{l}2{\varsigma }_{\mathrm{ij}}({\tilde{\mu }}_B+P_z{(2\epsilon )}^{-1/2})\mathrm{if\epsilon }>{\epsilon }_o\\ 2{\varsigma }_{\mathrm{ij}}({\tilde{\mu }}_B+P_z{(2{\epsilon }_0)}^{-1/2})\mathrm{if\epsilon }<{\epsilon }_o\end{array},$(1) For $\epsilon >{\epsilon }_o$, i.e. Casson fluid, we have

${\mu }^{\ast }={\tilde{\mu }}_B+P_z/\sqrt{2\epsilon }\text{and}\vartheta =\frac{{\tilde{\mu }}_B}{\rho }(1+{\beta }^{-1})$, here $\beta \left(={\tilde{\mu }}_B\sqrt{2\epsilon }{(P_z)}^{-1}\right)$ named as Casson factor.

Here, $(i,j{)}^{\mathrm{th}}$ component of stress tensor is denoted by ${\tau }_{\mathrm{ij}}$, absolute viscosity by ${\mu }^{\ast }$, non-Newtonian fluid plastic viscosity as ${\tilde{\mu }}_B$, kinematic viscosity as $\vartheta$, $\epsilon (={\varsigma }_{\mathrm{ij}}{\varsigma }_{\mathrm{ij}})$ is the product of deformation rate, ${\epsilon }_o$ is the critical value of the product and ${\varsigma }_{\mathrm{ij}}$ is the deformation rate, respectively.

2.3. Governing equations

Based on boundary layer assumptions and Tiwari-Das model [53] along with aforesaid assumptions, the fluid flow governing expressions can be written as [51,54,55] and [49]: (2) $\begin{array}{rl}\mathrm{\nabla }.V& =0,\end{array}$(2) (3) $\begin{array}{rl}{\rho }_{\mathrm{nf}}(V.\mathrm{\nabla })& ={\mu }_{\mathrm{nf}}\left(1+\frac{1}{\beta }\right)({\mathrm{\nabla }}^{2}V)+(J\times B{)}_x,\end{array}$(3) (4) $\begin{array}{rl}(\rho C_P{)}_{\mathrm{nf}}(V.\mathrm{\nabla T})& =-\mathrm{\nabla }\tilde{q}.\end{array}$(4)

The velocity field is expressed as (5) $V=[u,v,0],$(5) where the velocities $u,v$ are the function of $x$ and $y$.

Using the above condition, ${\varsigma }_{\mathrm{ij}}$ is given as (6) $2{\varsigma }_{\mathrm{ij}}=\left[\begin{array}{cc}2u_x& u_y+v_x\\ u_y+v_x& 2v_y\end{array}\right].$(6) Using Equation (5), then Equations (1) and (2) become (7) $\begin{array}{rl}{u}_x+v_y& =0,\end{array}$(7) (8) $\begin{array}{rl}u{u}_x+v{u}_y& ={\vartheta }_{\mathrm{nf}}\left(1+\frac{1}{\beta }\right)u_{\mathrm{yy}}+\frac{1}{{\rho }_{\mathrm{nf}}}(J\times B{)}_x.\end{array}$(8) Now, the magnetic field $B$, which is characterized by its components $(0,B_o,0)$ with $B_o$ a non-negative constant, ensures that the relation $\mathrm{\nabla }.B=0$ is inherently grasp. It is observed that the electric current inside the flow exhibits a perpendicular orientation with respect to the plane of the flow. Therefore, by using Ohm’s rule, we can get the component of $J$ as (9) ${\tilde{j}}_x=0,{\tilde{j}}_y=0,{\tilde{j}}_z={\sigma }_{\mathrm{nf}}[{\overline{E}}_z+{(V\times B)}_z]={\sigma }_{\mathrm{nf}}[{\overline{E}}_z+u{B}_o],$(9) where ${\overline{E}}_z$ is a part of the electric field that is oriented in the $z-$direction. Then by Maxwell’s equation for study flow: (10) $\mathrm{\nabla }\times \overline{E}=0,$(10) where $\overline{E}$ denotes the electric field in $z-$axis. Then from Equation (5), we get $\frac{\mathrm{\partial }{\overline{E}}_z}{\mathrm{\partial }y}=0$ and $\frac{\mathrm{\partial }{\overline{E}}_z}{\mathrm{\partial }x}=0$.

Applying the term of Equation (9) in Equation (8). Then we get (11) $u{u}_x+v{u}_y={\vartheta }_{\mathrm{nf}}\left(1+\frac{1}{\beta }\right)u_{\mathrm{yy}}-\frac{{\sigma }_{\mathrm{nf}}}{{\rho }_{\mathrm{nf}}}{B}_o^{2}u-\frac{{\sigma }_{\mathrm{nf}}}{{\rho }_{\mathrm{nf}}}{B}_o{\overline{E}}_z,$(11) For inviscid free stream condition, we can write $\frac{{\sigma }_{\mathrm{nf}}}{{\rho }_{\mathrm{nf}}}{B}_o^{2}U-\frac{{\sigma }_{\mathrm{nf}}}{{\rho }_{\mathrm{nf}}}{B}_o{\overline{E}}_z=0\Rightarrow {\overline{E}}_z=-B_{o}U$

In this model, the free stream velocity $U=0$. Now Equation (11) becomes (12) $u{u}_x+v{u}_y={\vartheta }_{\mathrm{nf}}\left(1+\frac{1}{\beta }\right)u_{\mathrm{yy}}-\frac{{\sigma }_{\mathrm{nf}}}{{\rho }_{\mathrm{nf}}}{B}_o^{2}u.$(12) The mechanism of heat transfer, i.e. Equation (4) modelled using the Cattaneo–Christov (CC) heat flux model, the expression for heat flux $(\tilde{q})$ in terms of CC model is given by (13) $\tilde{q}+{\tau }_o\left[\frac{\mathrm{\partial }\tilde{q}}{\mathrm{\partial }t}+(\mathrm{\nabla }.V)\tilde{q}-\tilde{q}.\mathrm{\nabla V}+V.\mathrm{\nabla }\tilde{q}\right]=-\kappa \mathrm{\nabla T},$(13)

As the considered flow is steady $\frac{\mathrm{\partial }\tilde{q}}{\mathrm{\partial }t}=0$ and $\mathrm{\nabla }.V=0$, Equation (13) reduces to (14) $\tilde{q}+{\tau }_o[V.\mathrm{\nabla }\tilde{q}-\tilde{q}.\mathrm{\nabla V}]=-\kappa \mathrm{\nabla T},$(14) Now eliminating $\tilde{q}$ between Equations (4) and (14), using Equation (5) and accounting the heating due to magnetic field and a non-uniform heat source/sink, we obtain (15) $\begin{array}{rl}& (\rho C_P{)}_{\mathrm{nf}}\\ & \times \left[(u{T}_x+v{T}_y)+{\tau }_o\left[\begin{array}{l}(u{u}_x+v{u}_y)T_x+u^2{T}_{\mathrm{xx}}\\ +2\mathrm{uv}{T}_{\mathrm{xy}}\\ +(u{v}_x+v{v}_y)T_y+v^2{T}_{\mathrm{yy}}\end{array}\right]\right]\\ & ={\kappa }_{\mathrm{nf}}{T}_{\mathrm{yy}}+\tilde{Q}+{\sigma }_{\mathrm{nf}}{B}_o^2{u}^2.\end{array}$(15) The second term on the R.H.S. of Equation (3) defined non-uniform heat source/sink term and is given as [56] (16) $\tilde{Q}=\frac{{\kappa }_{\mathrm{nf}}{U}_s(T_s-T_{\mathrm{\infty }})}{x{\vartheta }_{\mathrm{nf}}}\left[A^{\ast }{F}^{\mathrm{\prime }}+B^{\ast }\left(\frac{T-T_{\mathrm{\infty }}}{T_s-T_{\mathrm{\infty }}}\right)\right].$(16) For heat source, $A^{\ast }\text{and}{B}^{\ast }$ are non-negative and for heat sink both are negative.

Putting Equation (16) in Equation (15), we get (17) $\begin{array}{rl}& u{T}_x+v{T}_y+{\tau }_o[(u{u}_x+v{u}_y)T_x+(u{v}_x+v{v}_y)T_y+2\mathrm{uv}{T}_{\mathrm{xy}}\\ & +u^2{T}_{\mathrm{xx}}+v^2{T}_{\mathrm{yy}}]\\ & =\frac{1}{{(\rho C_P)}_{\mathrm{nf}}}\\ & \times [{\kappa }_{\mathrm{nf}}{T}_{\mathrm{yy}}+\frac{{\kappa }_{\mathrm{nf}}{U}_s(x)(T_s-T_{\mathrm{\infty }})}{x{\vartheta }_{\mathrm{nf}}}\\ & \times \left[A^{\ast }{F}^{\mathrm{\prime }}+B^{\ast }\left(\frac{T-T_{\mathrm{\infty }}}{T_s-T_{\mathrm{\infty }}}\right)\right]+{\sigma }_{\mathrm{nf}}{B}_0^2{u}^2].\end{array}$(17) Conditions at the surface (initial) and at boundary are (18) $\begin{array}{l}u=U_s=\mathrm{cx},v=-V_w,T_y=-\frac{\hslash }{{\kappa }_{\mathrm{nf}}}(T_s-T)\text{at}y=0,\\ u=U\to 0,T\to T_{\mathrm{\infty }}\text{as}y\to \mathrm{\infty }.\end{array}\}$(18) In above expressions the symbols ${\tau }_o,c,V_w,\hslash$ denote relaxation time for heat flux, constant, convective heat transfer coefficient, respectively.

In this study, single-phase nanofluid model is utilized and the physical terms are computed from the following relations [38]:

1. Density ${\rho }_{\mathrm{nf}}=(1-{\varphi }_{\mathrm{Au}}){\rho }_{\mathrm{Blood}}+{\varphi }_{\mathrm{Au}}{\rho }_{\mathrm{Au}}$

2. Heat capacity $(\rho C_P{)}_{\mathrm{nf}}=(1-{\varphi }_{\mathrm{Au}})(\rho C_P{)}_{\mathrm{Blood}}+{\varphi }_{\mathrm{Au}}(\rho C_P{)}_{\mathrm{Au}}$

3. Electrical conductivity ${\sigma }_{\mathrm{nf}}={\sigma }_{\mathrm{Blood}}\left[\frac{({\sigma }_{\mathrm{Au}}+2{\sigma }_{\mathrm{Blood}})+2{\varphi }_{\mathrm{Au}}({\sigma }_{\mathrm{Au}}-{\sigma }_{\mathrm{Blood}})}{({\sigma }_{\mathrm{Au}}+2{\sigma }_{\mathrm{Blood}})-{\varphi }_{\mathrm{Au}}({\sigma }_{\mathrm{Au}}-{\sigma }_{\mathrm{Blood}})}\right]$

4. Dynamic viscosity

   1. For cylindrical shaped Au nanoparticles: ${\mu }_{\mathrm{nf}}={\mu }_{\mathrm{Blood}}[1+13.5{\varphi }_{\mathrm{Au}}+904.4{({\varphi }_{\mathrm{Au}})}^2]$

   2. For blade shaped Au nanoparticles: ${\mu }_{\mathrm{nf}}={\mu }_{\mathrm{Blood}}[1+14.6{\varphi }_{\mathrm{Au}}+123.3{({\varphi }_{\mathrm{Au}})}^2]$

   3. For platelet shaped Au nanoparticles: ${\mu }_{\mathrm{nf}}={\mu }_{\mathrm{Blood}}[1+37.1{\varphi }_{\mathrm{Au}}+612.6{({\varphi }_{\mathrm{Au}})}^2]$

5. Thermal conductivity

   1. For cylindrical shaped Au nanoparticles: ${\kappa }_{\mathrm{nf}}={\kappa }_{\mathrm{Blood}}\left[\frac{{\kappa }_{\mathrm{Au}}+5.9{\kappa }_{\mathrm{Blood}}-5.9{\varphi }_{\mathrm{Au}}({\kappa }_{\mathrm{Blood}}-{\kappa }_{\mathrm{Au}})}{{\kappa }_{\mathrm{Au}}+5.9{\kappa }_{\mathrm{Blood}}+{\varphi }_{\mathrm{Au}}({\kappa }_{\mathrm{Blood}}-{\kappa }_{\mathrm{Au}})}\right]$

   2. For blade shaped Au nanoparticle: ${\kappa }_{\mathrm{nf}}={\kappa }_{\mathrm{Blood}}\left[\frac{{\kappa }_{\mathrm{Au}}+9.6{\kappa }_{\mathrm{Blood}}-9.6{\varphi }_{\mathrm{Au}}({\kappa }_{\mathrm{Blood}}-{\kappa }_{\mathrm{Au}})}{{\kappa }_{\mathrm{Au}}+9.6{\kappa }_{\mathrm{Blood}}+{\varphi }_{\mathrm{Au}}({\kappa }_{\mathrm{Blood}}-{\kappa }_{\mathrm{Au}})}\right]$

   3. For platelet shaped Au nanoparticles: ${\kappa }_{\mathrm{nf}}={\kappa }_{\mathrm{Blood}}\left[\frac{{\kappa }_{\mathrm{Au}}+6.7{\kappa }_{\mathrm{Blood}}-6.7{\varphi }_{\mathrm{Au}}({\kappa }_{\mathrm{Blood}}-{\kappa }_{\mathrm{Au}})}{{\kappa }_{\mathrm{Au}}+6.7{\kappa }_{\mathrm{Blood}}+{\varphi }_{\mathrm{Au}}({\kappa }_{\mathrm{Blood}}-{\kappa }_{\mathrm{Au}})}\right]$

The similarity variables are defined as [49]: (19) $\begin{array}{rl}\psi & =\sqrt{c{\vartheta }_{\mathrm{Blood}}}\mathrm{xF}(\xi ),\xi =y\sqrt{\frac{c}{{\vartheta }_{\mathrm{Blood}}}},\mathrm{\Theta }=\frac{T-T_{\mathrm{\infty }}}{T_s-T_{\mathrm{\infty }}},\\ u& =\frac{\mathrm{\partial }\psi }{\mathrm{\partial }y},v=-\frac{\mathrm{\partial }\psi }{\mathrm{\partial }x}.\end{array}$(19) Here, $\psi ,\xi ,F(\xi )\text{and}\mathrm{\Theta }(\xi )$ denote stream function, similarity variable, dimensionless velocity and dimensionless temperature, respectively.

Now, using the similarity transformation Equation (19) along with effective thermophysical properties correlations, Equation (7) is gratified identically and Equations (12) and (15) reduced to the following dimensionless form: (20) $\left(1+\frac{1}{\beta }\right)F^{\mathrm{\prime \prime \prime }}-\frac{{\lambda }_2}{{\lambda }_1}(F^{\mathrm{\prime }}{F}^{\mathrm{\prime }}-F{F}^{\mathrm{\prime \prime }})-\frac{{\lambda }_3}{{\lambda }_1}\mathrm{Mn}{F}^{\mathrm{\prime }}=0,$(20) (21) $\begin{array}{rl}& {\mathrm{\Theta }}^{\mathrm{\prime \prime }}+\frac{{\lambda }_2}{{\lambda }_1}(A\ast F^{\mathrm{\prime }}+B\ast \mathrm{\Theta })+\frac{{\lambda }_3}{{\lambda }_5}\mathrm{MnEcPr}(F^{\mathrm{\prime }}{)}^2\\ & +\frac{{\lambda }_4}{{\lambda }_5}\mathrm{Pr}[F{\mathrm{\Theta }}^{\mathrm{\prime }}-\tau [F{F}^{\mathrm{\prime }}{\mathrm{\Theta }}^{\mathrm{\prime }}+F^2{\mathrm{\Theta }}^{\mathrm{\prime \prime }}]]=0.\end{array}$(21) and subsequently Equation (18) becomes (22) $\begin{array}{l}F=S,F^{\mathrm{\prime }}=1,{\mathrm{\Theta }}^{\mathrm{\prime }}=\frac{-\mathrm{Bi}}{{\lambda }_5}[1-\mathrm{\Theta }]\mathrm{as\xi }=0,\\ F^{\mathrm{\prime }}\to 0,\mathrm{\Theta }\to 0\mathrm{when}\xi \to \mathrm{\infty }.\end{array}\}$(22) Here, the symbols $\mathrm{Mn},\mathrm{Pr},\mathrm{Ec},S(>0)$ stand for magnetic field, Prandtl number, Eckert number and suction, respectively and ${\lambda }_1,{\lambda }_2,{\lambda }_3,{\lambda }_4\text{and}{\lambda }_5$ are constants, and are defined as (23) $\begin{array}{r}\begin{array}{l}\mathrm{Mn}=\frac{{\sigma }_{\mathrm{Blood}}}{c{\rho }_{\mathrm{Blood}}}{B}_o^2,\mathrm{Pr}=\frac{{\mu }_{\mathrm{Blood}}{(C_p)}_{\mathrm{Blood}}}{{\kappa }_{\mathrm{Blood}}},\\ \mathrm{Ec}=\frac{c^2{x}^2}{(T_w-T_{\mathrm{\infty }}){(C_p)}_{\mathrm{Blood}}},S=\frac{V_w}{\sqrt{c{\vartheta }_{\mathrm{Blood}}}},\\ \mathrm{Bi}=(\hslash /{\kappa }_{\mathrm{Blood}}){\left(\frac{{\vartheta }_{\mathrm{Blood}}}{c}\right)}^{1/2},{\lambda }_1=({\mu }_{\mathrm{nf}}/{\mu }_{\mathrm{Blood}}),\\ {\lambda }_2=({\rho }_{\mathrm{nf}}/{\rho }_{\mathrm{Blood}}),{\lambda }_3=({\sigma }_{\mathrm{nf}}/{\sigma }_{\mathrm{Blood}}),\\ {\lambda }_4=({(\rho C_P)}_{\mathrm{nf}}/{(\rho C_P)}_{\mathrm{Blood}}),{\lambda }_5=({\kappa }_{\mathrm{nf}}/{\kappa }_{\mathrm{Blood}}).\end{array}\}\end{array}$(23)

2.4. Variables of engineering importance

The SFC and LNN are physical variables and these are defined as (24) $\begin{array}{rl}{C}_{\mathrm{fx}}& ={\frac{{\mu }_{\mathrm{nf}}}{{\rho }_{\mathrm{Blood}}}\left(1+\frac{1}{\beta }\right)\frac{\mathrm{\partial }u}{\mathrm{\partial }y}|}_{y=0}\text{and}\\ N{u}_x& =\frac{-x}{{\kappa }_{\mathrm{Blood}}(T_s-T_{\mathrm{\infty }})}{\kappa }_{\mathrm{nf}}{\frac{\mathrm{\partial }T}{\mathrm{\partial }\text{y}}|}_{y=0}\end{array}$(24) Using (19), and necessary correlations for ${\mu }_{\mathrm{nf}}\text{and}{\kappa }_{\mathrm{nf}}$, the non-dimensional form of SFC and LNN is (25) $\begin{array}{rl}R{e}_x^{0.5}{C}_{\mathrm{fx}}& ={\lambda }_1\left(1+\frac{1}{\beta }\right)F^{\mathrm{\prime \prime }}(\xi =0)\text{and}R{e}_x^{-0.5}N{u}_x\\ & =-{\lambda }_5{\mathrm{\Theta }}^{\mathrm{\prime }}(\xi =0).\end{array}$(25)

3. Fuzzy differential equations (FDEs)

3.1. Definition

A fuzzy set B in Y is considered by a membership function µ_B(x), which takes the values in [0, 1]. Thus set B in Y is expressed as in terms of ordered pairs. Every pair contains a generic element x and µ_B(x) and fuzzy set is expressed as

$B=\{(x_i,{\mu }_B(x_i)):x_i\in Y\}.$

where µ_B(x_i) is known as grade of membership of x_i in B, which maps Y to the interval [0, 1].

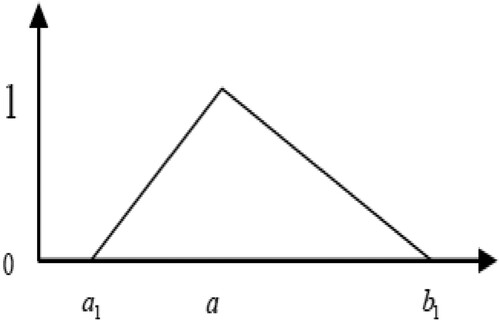
3.2. Triangular membership function

(26) ${\mu }_B(x)=\{\begin{array}{ccc}0;& & \mathrm{if}x\le a_1\\ {\displaystyle \frac{x-a_1}{a-a_1}};& & \mathrm{if}{a}_1\le x\le a\\ {\displaystyle \frac{b_1-x}{b_1-a}};& & \mathrm{if}a\le x\le b_1\\ 0;& \mathrm{if}& b_1\le x\end{array}.$(26)

3.3. Fuzzification

It has been observed that changes in the VFN “Volume Fraction of Nanoparticles” can have an impact on the thermal field and velocity outlines of nanofluids and hybrid nanofluids. This behaviour of nanofluids led us to consider volume fraction as a fuzzy parameter represented by triangular fuzzy numbers (TFNs), see Table 2. Consequently, the present problem is investigated by assuming the VFN as a TFN (see Figure 2). The governing ordinary differential equations (see Equations 20–22) are transformed into fuzzy differential equations using the α-cut technique of fuzzy numbers. The α-cut value ranges from 0 to 1 and determines the level of fuzziness in the TFN. (27) $\begin{array}{rl}& \left(1+\frac{1}{\beta }\right)\frac{d^3}{d{\xi }^3}[{\stackrel{⌢}{F}}_1(\xi ,\alpha ),{\stackrel{⌢}{F}}_2(\xi ,\alpha )]\\ & -\frac{{\lambda }_2}{{\lambda }_1}\left\{\begin{array}{l}{\left({\displaystyle \frac{d}{\mathrm{d\xi }}}[{\stackrel{⌢}{F}}_1(\xi ,\alpha ),{\stackrel{⌢}{F}}_2(\xi ,\alpha )]\right)}^2\\ -([{\stackrel{⌢}{F}}_1(\xi ,\alpha ),{\stackrel{⌢}{F}}_2(\xi ,\alpha )])\\ \left({\displaystyle \frac{d^2}{d{\xi }^2}}[{\stackrel{⌢}{F}}_1(\xi ,\alpha ),{\stackrel{⌢}{F}}_2(\xi ,\alpha )]\right)\end{array}\right\}\\ & -{\displaystyle \frac{{\lambda }_3}{{\lambda }_1}}\mathrm{Mn}{\displaystyle \frac{d}{\mathrm{d\xi }}}[{\stackrel{⌢}{F}}_1(\xi ,\alpha ),{\stackrel{⌢}{F}}_2(\xi ,\alpha )]=0,\end{array}$(27) (28) $\begin{array}{rl}& \frac{d^2}{d{\xi }^2}[{\stackrel{⌢}{\mathrm{\Theta }}}_1(\xi ,\alpha ),{\stackrel{⌢}{\mathrm{\Theta }}}_2(\xi ,\alpha )]\\ & +\frac{{\lambda }_2}{{\lambda }_1}A\ast \left(\frac{d}{\mathrm{d\xi }}[{\stackrel{⌢}{F}}_1(\xi ,\alpha ),{\stackrel{⌢}{F}}_2(\xi ,\alpha )]\right)\\ & +\frac{{\lambda }_2}{{\lambda }_1}B\ast [{\stackrel{⌢}{\mathrm{\Theta }}}_1(\eta ,\alpha ),{\stackrel{⌢}{\mathrm{\Theta }}}_2(\eta ,\alpha )]\\ & +\frac{{\lambda }_3}{{\lambda }_5}\mathrm{MnEc}Pr{\left(\frac{d}{\mathrm{d\xi }}[{\stackrel{⌢}{F}}_1(\xi ,\alpha ),{\stackrel{⌢}{F}}_2(\xi ,\alpha )]\right)}^2\\ & +\frac{{\lambda }_4}{{\lambda }_5}Pr[{\stackrel{⌢}{F}}_1(\xi ,\alpha ),{\stackrel{⌢}{F}}_2(\xi ,\alpha )]\left(\frac{d}{\mathrm{d\xi }}[{\stackrel{⌢}{\mathrm{\Theta }}}_1(\xi ,\alpha ),{\stackrel{⌢}{\mathrm{\Theta }}}_2(\xi ,\alpha )]\right)\\ & -\frac{{\lambda }_4}{{\lambda }_5}Pr\tau \left\{\begin{array}{l}[{\stackrel{⌢}{F}}_1(\xi ,\alpha ),{\stackrel{⌢}{F}}_2(\xi ,\alpha )]\\ \left({\displaystyle \frac{d}{\mathrm{d\xi }}}[{\stackrel{⌢}{F}}_1(\xi ,\alpha ),{\stackrel{⌢}{F}}_2(\xi ,\alpha )]\right)\\ \left({\displaystyle \frac{d}{\mathrm{d\xi }}}[{\stackrel{⌢}{\mathrm{\Theta }}}_1(\xi ,\alpha ),{\stackrel{⌢}{\mathrm{\Theta }}}_2(\xi ,\alpha )]\right)\\ +[{\stackrel{⌢}{F}}_1(\xi ,\alpha ),{\stackrel{⌢}{F}}_2(\xi ,\alpha ){]}^2\\ \left({\displaystyle \frac{d^2}{d{\xi }^2}}[{\stackrel{⌢}{\mathrm{\Theta }}}_1(\xi ,\alpha ),{\stackrel{⌢}{\mathrm{\Theta }}}_2(\xi ,\alpha )]\right)\end{array}\right\}=0.\end{array}$(28) with conditions: (29) $\begin{array}{rl}& [{\stackrel{⌢}{F}}_1(0,\alpha ),{\stackrel{⌢}{F}}_2(0,\alpha )]\\ & =[S,S],\frac{d}{\mathrm{d\xi }}[{\stackrel{⌢}{F}}_1(0,\alpha ),{\stackrel{⌢}{F}}_2(0,\alpha )]=[1,1],\end{array}$(29) (30) $\begin{array}{rl}& \frac{d}{\mathrm{d\xi }}[{\stackrel{⌢}{\mathrm{\Theta }}}_1(0,\alpha ),{\stackrel{⌢}{\mathrm{\Theta }}}_2(0,\alpha )]\\ & =-\frac{\mathrm{Bi}}{{\lambda }_5}\{1-[{\stackrel{⌢}{\mathrm{\Theta }}}_1(0,\alpha ),{\stackrel{⌢}{\mathrm{\Theta }}}_2(0,\alpha )]\},\end{array}$(30) (31) $\begin{array}{rl}& \frac{d}{\mathrm{d\xi }}[{\stackrel{⌢}{F}}_1(\eta ,\alpha ),{\stackrel{⌢}{F}}_2(\eta ,\alpha )]\to [0,0],[{\stackrel{⌢}{\mathrm{\Theta }}}_1(\eta ,\alpha ),{\stackrel{⌢}{\mathrm{\Theta }}}_2(\eta ,\alpha )]\\ & \to [0,0]\text{when}\eta \to \mathrm{\infty }.\end{array}$(31)

Figure 2. Representation of TFN.

Table 2. TFNs of volume fraction.

Fuzzy parameter	Crisp value	TFNs	$\alpha$- cut approach
${\varphi }_s$	[0.01–0.04]	[0, 0.04, 0.08]	[0.04$\alpha$, 0.08–0.04$\alpha$]

4. Results and discussion

Casson nanofluid flow through a stretching sheet is presented in this article. Gold nanoparticles are considered with cylindrical, platelet and blade-shaped nanoparticles in the blood to show the behaviour of the several physical properties. The proposed designed model is transformed to the nonlinear ordinary set of DEs by imposing standard transformation rules. First of all, the higher order equations get converted to the set of first-order equations. Further, these are tackled numerically by adopting traditional Runge–Kutta fourth-order technique combined with shooting. At the time of computation, the total number of nodal points is taken as 101 for the convergence of the methodology. The CPU time also reported as 0.1439 s to get an accuracy of 10⁻⁶. The novelty of the study is due to the fuzzified velocity and temperature outlines for the fuzzified volume fraction. Therefore, triangular fuzzy membership function is defined and described briefly. The computation is carried out by setting standard values of the characterizing parameters keeping fixed within their range as $\mathrm{Ec}=0.5,\tau =0.01,A^{\ast }=0.25=B^{\ast }$. The present result is validating with the work of [57] and [58] with a good agreement and the numerical outcomes are publicized in Table 3. This correlate result shows the convergence criteria of the proposed methodology. Further, the behaviour of the characterizing constraints is presented through Figures 3(a–b)–12(a–b) and elaborated with physical description clearly.

Figure 3. Impact of $\mathrm{Mn}$ on velocity profiles for (a) suction and (b) injection.

Table 3. Comparison of $-{\mathrm{\Theta }}^{\mathrm{\prime }}(\xi =0)$ for distinct $\mathrm{Pr}$ when ${\varphi }_{\mathrm{Au}}=0$.

$\mathrm{Pr}$	Wang [57]	Gorla and Sidawi [58]	Present outcomes
0.07	0.0656	0.0656	0.066825
2.0	0.9114	0.9114	0.902758
7.0	1.8954	1.8905	1.902541

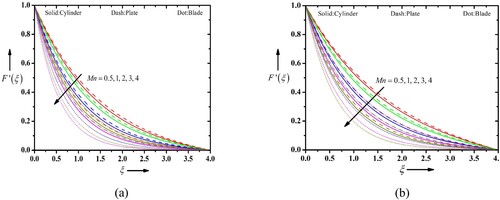
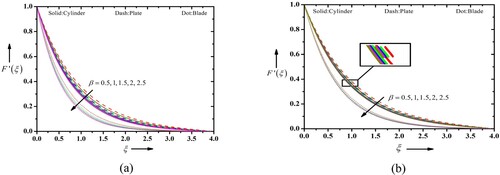
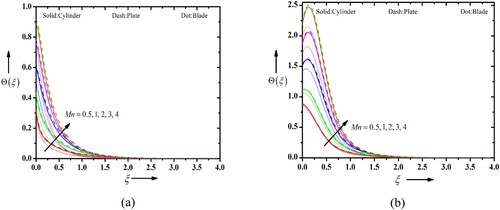
Figure 3 defines the velocity profiles of Casson blood nanofluid in the existence of a magnetic field Mn for the various cases such as (a) suction and (b) injection. Further, the analysis is deployed for the consideration of different particle shapes of the gold nanoparticles, i.e. cylindrical, platelet and blade shaped particles. When Mn is functional to a fluid flow, it introduces a Lorentz force that interacts with the fluid motion. The magnetic parameter, often represented by the symbol Mn, quantifies the strength of the applied magnetic field and its influence on the fluid flow. In the case of Casson blood nanofluid flow with suction/injection, the magnetic parameter affects the velocity profile greatly. Growing the Mn tends to decrease the flow velocity and this magnetic field creates a retarding force that discard the fluid motion, resulting in reduced velocities. The magnetic field has a stabilizing influence on the flow. Higher values of Mn increase the stability of the flow by suppressing fluid instabilities such as turbulence or secondary flow patterns. This can result in a more regular and ordered velocity profiles. In both the case of suction/injection, the profile behaves in similar trend. Further, in comparative analysis, the platelet shape is more pronounced than the cylindrical and blade shape particles. The Casson parameter is an important variable that characterizes the rheological performance of non-Newtonian fluids, including blood nanofluids which are publicized in Figure 4(a and b). The Casson variable distresses the velocity profiles in combination with other factors such as the stretching parameter, suction/injection parameter and the type of nanoparticles (cylindrical, platelet or blade-shaped). The Casson model describes the non-Newtonian behaviour of fluids by considering a yield stress with plastic viscosity. Then yield stress signifies the least stress essential for the fluid to start flowing, while the plastic viscosity characterizes the resistance to flow. When considering the upshot of the Casson variable on the velocity outlines, a higher Casson parameter leads to an increased yield stress and plastic viscosity. This results in a more pronounced deviation from the Newtonian behaviour, where the velocity near the wall is lower compared to Newtonian fluids. In the case of suction, where fluid is being removed from the flow, a higher Casson variable tends to condense the velocity near the wall, resulting in a thinner boundary layer and faster flow in the bulk of the fluid. Conversely, for injection, where fluid is being introduced into the flow, a higher Casson variable leads to escalate in velocity near the wall, resulting in a thicker boundary layer and slower flow in the bulk of the fluid. The type of nanoparticles (cylindrical, platelet or blade-shaped) also influences the velocity profiles of the Casson blood nanofluid. The presence of nanoparticles can alter the effective viscosity of the nanofluid and modify the velocity distribution. The exact consequence of nanoparticle shape on the velocity profiles would base on the specific characteristics of the nanoparticles, like their size, orientation and concentration. Figure 5(a and b) portray the role of Mn on the temperature profiles of Casson blood nanofluid flow in the occurrence of suction and injection, considering different types of nanoparticles (cylindrical, platelet and blade-shaped). The stretching velocity and temperature at the sheet surface is a crucial parameter. The occurrence of suction or injection at the sheet affects the boundary conditions, and the type and shape of nanoparticles influence the properties of the nanofluid. The Mn represents the strength of magnetic field relative to other governing parameters. A higher Mn implies a tougher magnetic field. The magnetic field can influence the motion and orientation of nanoparticles in the nanofluid. The orientation and distribution of nanoparticles under the impact of a magnetic field can affect the effective thermal conductivity and viscosity of the nanofluid. The temperature profiles may be influenced. Additionally, the magnetic field can generate Joule heating within the nanofluid, which contributes to the overall temperature distribution. To acquire a comprehensive considerate of the specific impact of Mn on the temperature outlines, one would need to consider the coupled equations of fluid flow, heat transfer and nanoparticle motion. This typically involves solving a set of PDEs numerically using apt boundary conditions and physical properties for the nanofluid. It is worth perceiving that the specific effects of different types of nanoparticles (cylindrical, platelet and blade-shaped) on the temperature profiles would depend on their respective geometries, thermal conductivities and shapes. These parameters can influence the convective heat transfer characteristics and thermal dispersion within the nanofluid.

Figure 4. Impact of $\beta$ on velocity profiles for (a) suction and (b) injection.

Figure 5. Impact of $\mathrm{Mn}$ on temperature profiles for (a) suction and (b) injection.

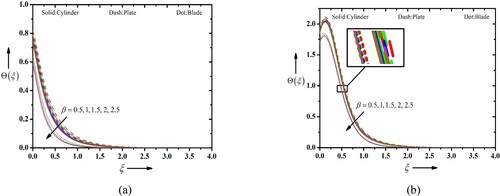
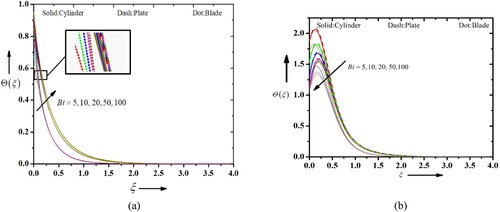
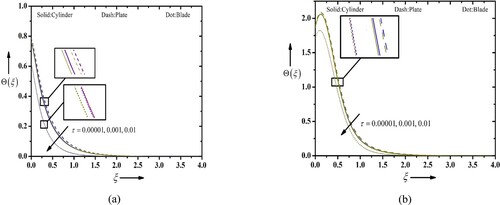
Figure 6(a and b) depicts the behaviour of the Casson parameter, a rheological parameter, which characterizes the behaviour of non-Newtonian fluids on the temperature profiles. It takes into account the yield stress and the apparent viscosity of the fluid. Upon studying the temperature profile of Casson blood nanofluid flow in the existence of suction/injection, the Casson parameter plays a noteworthy role in determining the heat transfer behaviour. The addition of nanoparticles to the Casson blood fluid introduces the concept of a nanofluid, which can further enhance heat transfer due to the augmented thermal conductivity of nanoparticles. In the present case, the cylindrical, platelet and blade-shaped nanoparticles are considered to exhibit their behaviour on the profiles. A higher Casson parameter corresponds to a higher yield stress in the Casson blood fluid. This leads to an increased resistance to flow, and subsequently, a decrease in the flow velocity near the stretching sheet. The reduced velocity gradient can result in a decreased convective heat transfer coefficient, leading to an advanced temperature near the surface. The presence of cylindrical, platelet or blade-shaped nanoparticles in the Casson blood nanofluid introduces additional parameters such as nanoparticle volume fraction, shape factor and thermal conductivity. These factors can affect the temperature profile by altering the effective thermal conductivity of the nanofluid and enhancing the convective heat transfer coefficient. Figure 7(a and b) demonstrates the impact of thermal Biot number, a dimensionless parameter that characterizes the relative rate of HT between a solid and a fluid, on the temperature profiles of existing fluid flow with suction and injection, considering different types of nanoparticles. When the thermal Biot number is small (Bi 1), it suggests that the heat transfer at the solid–fluid interface is much slower compared to the heat transfer within the solid. This implies that the solid takes longer to reach the fluid temperature, leading to a significant temperature gradient at the solid–fluid interface. In this case, the thermal resistance within the solid dominates the overall heat transfer, and the temperature profiles of the nanofluid flow are affected by both the fluid flow and the thermal characteristics of the solid. However, the platelet shaped particle displays a maximum impact on temperature in comparison to another shaped particle. The stimulus of the thermal relaxation variable on the temperature profiles is presented in Figure 8(a and b) considering cylindrical, platelet and blade-shaped nanoparticles. The thermal relaxation parameter signifies the ratio of thermal relaxation time to the characteristic flow time and determines the rate at which the fluid temperature adjusts to changes in the heat transfer conditions. A higher thermal relaxation parameter indicates a faster relaxation time, meaning the fluid temperature responds more rapidly to changes in the surrounding conditions. The shape of the nanoparticles, whether cylindrical, platelet or blade-shaped, influences their effective thermal conductivity and diffusivity. A higher thermal relaxation parameter leads to a more rapid temperature adjustment, causing a stronger retardation in the temperature profile.

Figure 6. Impact of $\beta$ on temperature profiles for (a) suction and (b) injection.

Figure 7. Impact of $\mathrm{Bi}$ on temperature profiles for (a) suction and (b) injection.

Figure 8. Impact $\tau$ on temperature profiles for (a) suction and (b) injection.

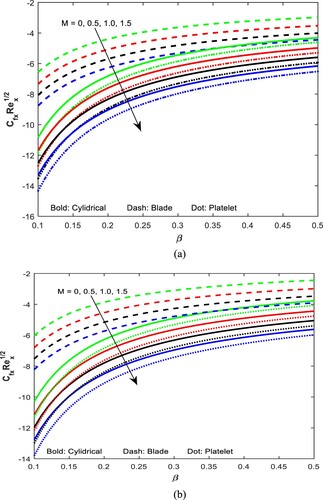
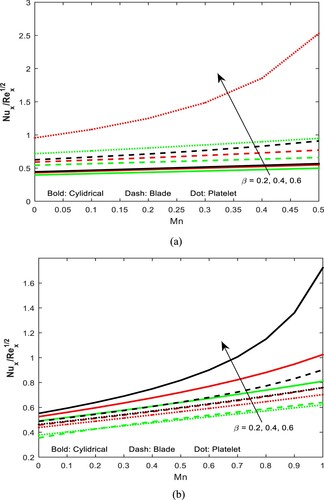
Figure 9(a and b) illustrate the influence of fuzzy volume fraction on the fuzzy velocity and temperature profiles of working fluid flow in the case of suction and injection can be analysed by considering cylindrical, platelet and blade-shaped nanoparticles. In this scenario, the fuzzy volume fraction refers to the uncertainty or imprecision associated with the nanoparticle concentration. When studying the flow of Casson blood nanofluid, which consists of blood as the base fluid and nanoparticles dispersed within it, several factors come into play. The shape and type of nanoparticles can affect the flow characteristics, while suction and injection influence the flow behaviour near the stretching sheet. The fuzzy volume fraction introduces uncertainty into the nanoparticle concentration, which further affects the flow properties. Incorporating the fuzzy volume fraction into the model requires dealing with uncertain or imprecise data. Fuzzy sets describe the fuzzy volume fraction, allowing for a range of possible values instead of a single precise value. Fuzzy logic is used to derive fuzzy rules and make approximate inferences to predict the flow behaviour. The analysis considered the specific characteristics of the cylindrical, platelet and blade-shaped nanoparticles. Each nanoparticle shape will have different effects on the flow, heat transfer and mixing characteristics of the nanofluid. Additionally, the suction and injection conditions should be taken into account to assess their impact on the flow properties near the stretching sheet. Figure 10(a and b) portrays the impact of the Casson parameter on the profiles of shear rate versus the magnetic parameter of Casson fluid flow over existing geometry sheet in the existence of suction and injection, considering cylindrical, platelet and blade-shaped nanoparticles. Analysing the shear rate profile can provide insights into the flow behaviour, including regions of high shear rate and low shear rate. It can also reveal the impact of the Casson parameter on the flow characteristics, such as the presence of recirculation zones, separation points or boundary layer development. The influence of different nanoparticle shapes (cylindrical, platelet, blade-shaped) can also be investigated by comparing the shear rate profiles obtained for each case. In both the case of suction and injection the result reveals that increasing Casson parameter enriches the profiles of shear rate but increasing magnetic parameter the strength of the profiles attenuates significantly. The blade shape nanoparticles show greater impact in enhancing the shear rate in comparison to the cylindrical as well as platelet shaped nanoparticles. The influence of magnetic parameter on the profiles of shear rate versus Casson parameter of Casson blood nanofluid flow in case of suction and injection can be studied in Figure 11(a and b). However, it is important to note that the specific details of the model, including the equations and boundary conditions, need to be defined to perform the analysis. The presence of cylindrical, platelet and blade-shaped nanoparticles is considered for the impact of magnetic parameter on the flow characteristics of these nanofluids. In terms of the nanoparticles, the specific shape (cylindrical, platelet or blade-shaped) would influence the rheological properties of the nanofluid, including the effective viscosity. This would need to be accounted for in the constitutive equations of the nanofluid, considering the nanoparticle shape and concentration. By varying the magnetic parameter, suction/injection parameters and Casson parameter, the shear rate profile varies in response to these parameters. Higher magnetization shows slower shear rate but increasing Casson parameter enhances the rate significantly. Figure 12(a and b) explore the behaviour of Casson parameter that affects the profiles of heat transfer rate in the case of a Casson blood nanofluid flow over a stretching sheet, considering different shapes of nanoparticles (cylindrical, platelet and blade shape). The Casson parameter represents the yield stress of the fluid and determines the flow characteristics. When considering the impact of the magnetic parameter, which represents the intensity of the applied magnetic field, the behaviour depends on the interaction between the magnetic field and the nanoparticles. Magnetic fields can affect the motion and distribution of nanoparticles in the nanofluid. The specific influence of the Casson parameter and the magnetic parameter on the heat transfer rate profiles would depend on the specific conditions, such as the values of these parameters, the shape and concentration of nanoparticles and the boundary conditions (suction or injection). However, in both the case of suction/injection it is seen that the platelet-shaped particle influences a greater impact to enhance the HTR in comparison to the blade and cylindrical shape nanoparticles respectively.

Figure 9. Impact of fuzzy volume fraction on (a) fuzzy velocity profiles and (b) fuzzy temperature profiles.

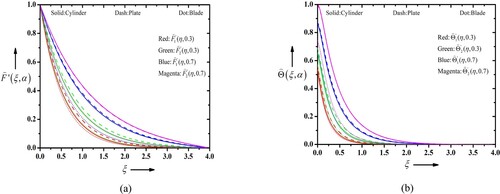
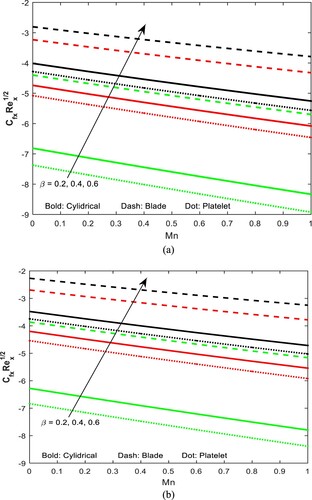
Figure 10. (a) Outline of SFC versus $\mathrm{Mn}$ for several values of $\beta$ for suction. (b) Outline of SFC versus $\mathrm{Mn}$ for several values of $\beta$ for injection.

Figure 11. (a) Outline of SFC versus $\beta$ for several values of $\mathrm{Mn}$ for suction. (b) Outline of SFC versus $\beta$ for several values of $\mathrm{Mn}$ for injection.

Figure 12. (a) Outline of LNN versus $\mathrm{Mn}$ for several values of $\beta$ for suction. (b) Outline of LNN versus $\mathrm{Mn}$ for several values of $\beta$ for injection.

5. Conclusion

The study on Casson blood nanofluid flow with suction and injection, considering cylindrical, platelet and blade-shaped nanoparticles, reveals several important findings. The variation in shape leads to changes in the fluid flow patterns, velocity profiles and temperature distribution along the stretching sheet. In concluding remarks, it is noted that:

• The inclusion of gold nanoparticles in the blood flow significantly affects the overall behaviour of the fluid by considering various shape of the nanoparticles such as cylindrical, platelet or blade-shaped.

• The presence of suction and injection further alters the flow dynamics. Suction enhances the flow rate, resulting in increased velocity near the sheet, while injection decreases the flow rate, leading to reduced velocity.

• The analysis of the Casson blood nanofluid flow reveals that the Casson parameter acting a decisive character for finding the flow behaviour. The Casson parameter represents the yield stress of the nanofluid and affects the boundary layer thickness and shear stress distribution.

• It seems that an escalation in the Casson parameter diminishes the boundary layer thickness and enhances the shear stress near the sheet.

• The shape of the nanoparticles significantly influences the thermal conductivity and viscosity of the nanofluid.

• The cylindrical nanoparticles exhibit the extreme thermal conductivity, followed by platelet and blade-shaped nanoparticles. Additionally, the viscosity of the nanofluid rises with the presence of nanoparticles, with cylindrical nanoparticles leading to the highest viscosity.

Overall, the investigation of Casson blood nanofluid flow over a stretching sheet in the context of suction and injection, considering cylindrical, platelet and blade-shaped nanoparticles, provides valuable insights into the complex fluid dynamics and heat transfer phenomena. These findings can contribute to the development of efficient cooling systems, biomedical applications and industrial processes involving nanofluids and blood-like fluids. Future research can focus on exploring additional nanoparticle shapes, considering other non-Newtonian models, and investigating the impact of other external factors.

Disclosure statement

No potential conflict of interest was reported by the author(s).