Joint stochastic optimisation of open-pit mine production scheduling with ramp design

ABSTRACT

Stochastic optimisation of open-pit mine production scheduling maximises the NPV of a mine’s extraction sequence while satisfying production constraints and minimising deviations from targets. Past approaches consider mining block access based on slope constraints, thus providing no guarantee that the infrastructure required for equipment access is feasible. To address this issue, a joint stochastic optimisation of life-of-mine production scheduling and ramp design is proposed, ensuring feasible equipment access to the related mining blocks. An application at a gold mine demonstrates the value of considering the complex relationship that exists between ramp design, equipment access and production scheduling during optimisation.

KEYWORDS:

• Open-pit mine production scheduling
• optimisation
• stochastic integer programming
• ramp design

1. Introduction

Open-pit mining is a large-scale extractive activity in which substantial quantities of material are excavated from a continually expanding pit and transported for further treatment. The transportation of mined material from its point of excavation to its next destination requires a road and ramp network, connecting mining locations to material destinations [1]. Ramps are usually placed adjacent to the pit wall and enable equipment to travel between benches, while roads enable equipment to traverse across flat terrain, such as a bench, or from the pit exit to the crusher. Typically, the ramp and road network is designed after the long-term production schedule has been optimised, as the schedule defines when and where equipment access is required. However, ramps and haul roads are relatively large pieces of infrastructure which not only affect the geometry of the pit defined by the long-term schedule but also the availability of material. The modifications required to accommodate a ramp and road network can decrease the performance of the long-term schedule, decreasing net present value (NPV). As a result of the co-dependence between the ramp and road design, sequential optimisation of either component individually can lead to sub-optimal results. In this work, the joint optimisation of the long-term production schedule and ramp and road design while ensuring feasible equipment access to scheduled mining blocks is proposed, to address the issues arising from the sequential process.

Conventionally, open-pit mine production schedules are formulated deterministically; however, orebodies are heterogeneous, and a single smooth estimate of the orebody provides no information about the variability and uncertainty of the material in the ground. Stochastic optimisation for open-pit mine production scheduling improves upon their deterministic counterparts by taking as input a set of geostatistical simulations [2], which represent the variability and uncertainty of material in the ground. Ramazan and Dimitrakopoulos [3] first proposed a two-stage stochastic integer program for open-pit mine production scheduling, which was limited to a single element mine without a stockpile. The value of the stochastic solution as it relates to mine production scheduling was then demonstrated by Dimitrakopoulos and Ramazan [4]. Since then, stochastic formulations for mine planning have been extended to include stockpiles [5], multiple elements [6,7] and entire mining complexes [8–12]. Simultaneously optimising entire mining complexes in the presence of uncertainty increases values, improves forecasts and reduces risk [8–15]. Concurrently, the optimisation of large stochastic problem has been extensively studied, leading to the development of many advanced heuristic methods [16–19], and smart solvers leveraging reinforcement learning [20]. However, in all past approaches, block access is defined solely through the slope constraints, and does not explicitly consider the ramp and road network required to facilitate equipment access to the scheduled mining blocks. As a result, the optimised production schedules require modification to accommodate the placement of ramps and roads, while ensuring feasible equipment access to scheduled mining blocks, affecting the value of the previously optimised solution.

Previous work to optimise ramp and road design considers it to be separate from open-pit mine production scheduling and has focused on optimising ramp design for a predefined ultimate pit limit (UPL). Gill [21] provides a dynamic programming approach, which optimises the ramp design for a given ultimate pit limit. The dynamic program discretizes ramps into single bench segments and identifies the combination of segments providing access from the surface to the lowest bench, while considering the cost of stripping additional material (expanding the predefined pit) and leaving material unmined (shrinking predefined pit). Nancel-Penard et al. [22] propose a method which takes as input a set of pre-defined pushbacks and generates an optimal ramp design considering the cost of additional blocks to be extracted, while also modifying the pushback design to provide space for ramp placement. Yarmuch et al. [23] optimise the design of both the ramp within the pit, and the ex-pit haul road, considering construction, haulage and maintenance costs. The ex-pit haul roads are optimised using a shortest path approach, while the ramp design is optimised via a binary linear program, which minimises the ramp costs. Morales et al. [24] develop a mathematical program which optimises the discretised pushback design, while ensuring adequate space between pushbacks for ramp placement and then uses an algorithm to construct an operational push back design. However, in all previously presented methods, the schedule is not informed by the placement of ramps and the accessibility which it provides. In an operating mine, equipment requires road access to all scheduled mining activities, meaning that mining is required to progress outwards from the ramp. The co-dependence of the schedule and ramp/road design means that any optimisation process which does not jointly consider both the schedule, and the ramp design results in a sub-optimal solution that does not leverage the relationship between the two components. In this study, the goal is to introduce a novel approach for jointly optimising open-pit mine production scheduling and ramp design. Accordingly, a two-stage stochastic integer program (SIP) [25] for optimising long-term open-pit mine production schedules while ensuring equipment access through ramps and road is presented. This differs from previous methods in that scheduling and ramp design are jointly considered under one mathematical formulation, rather than considering them separately in a stepwise approach as done in previous studies. The SIP builds upon the formulation presented in Ramazan and Dimitrakopoulos [5] to ensure feasible equipment access by requiring that all mined blocks be accessible from a road that leads to the top of the pit in the period in which they are mined. Roads are modelled as two separate components: intra-bench roads which facilitate traversal across benches, and ramps which facilitate traversal between benches similarly to Gill [21]. Intra-bench roads are constructed such that they join ramps to a set of predefined locations on each bench called checkpoints, and a block is considered accessible from that road if it is within the checkpoints window. Formulation of the SIP requires the set of all check-points, ramps and intra-bench roads to be predefined, which may be achieved through the pre-processing procedure presented below.

In the following section, the preprocessing procedures and the proposed stochastic mathematical program are first presented. Next, the method is applied to a gold mine, and results are discussed. Conclusions and directions for future work follow.

2. Method

This section presents a stochastic mathematical program which jointly optimises the long-term open-pit mine production schedule and ramp design under grade uncertainty, while ensuring feasible equipment access to scheduled mining blocks. First, checkpoints, ramps and intra-bench roads are discussed in more detail. Then, the notation, constants, sets and variables are presented, followed by the SIP.

2.1. Checkpoints

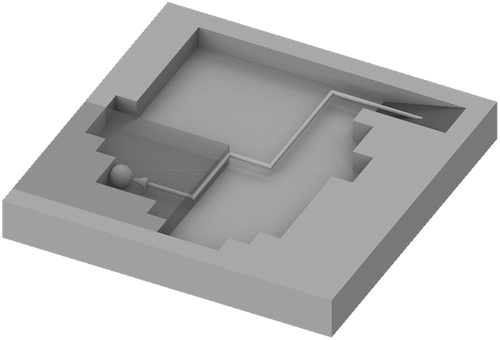
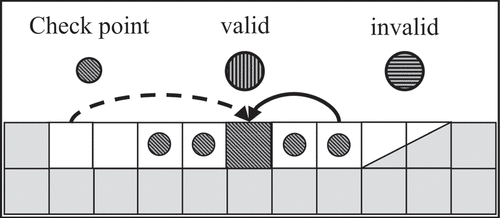
Checkpoints are regularly spaced nodes, which, when active, provide access to all mining blocks within their window. For a checkpoint to be active, there must exist a road connecting it to the top of the pit. An example of an active checkpoint is provided in Figure 1, where an isometric view of a bench containing a checkpoint, road and ramp is shown. The sphere represents the checkpoint node, and the shaded rectangular prism denotes the area which the checkpoint provides access to. The arrow represents the path through which a road may progress to reach and activate the checkpoint.

Figure 1. Isometric view of a bench depicting a checkpoint (sphere), accessible blocks (shaded volume), road (arrow) and ramp.

2.2. Ramp segments

Ramp segments are single bench ramps, modelled as a collection of mining blocks which approximate the true shape of the ramp. Modelling ramp segments as a collection of mining blocks allow ramp design decisions to be easily translated to the schedule and mining blocks which they effect. To fully define a ramp, the following components are required: location ($\mathit{i}$): index of the block at the top of the ramp, period ($\mathit{t}$): Time period when the ramp is present, and design ($\mathit{d}$): Set of blocks contained in the ramp.

2.3. Intra-bench roads

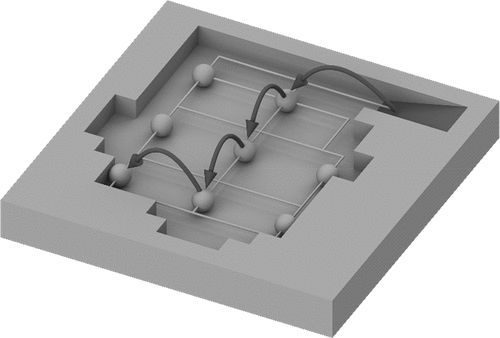
Intra-bench roads define the set of blocks connecting two points on the same bench and are modelled as the composition of sub- and super-roads. Sub-roads are short high-resolution paths, joining adjacent checkpoint nodes, while super-roads are long low-resolution paths joining blocks at large distances. Figure 2 shows an isometric view of a bench, with checkpoints, sub-roads and a super road. Sub-roads define the exact set of blocks through which the road progresses, while super roads define the general area through which a road must progress. In Figure 2, the super-road provides access to the bottom left most checkpoint, and the super-road may be traversed by any of the sub-roads connecting the checkpoints through which the super-road progresses. Modelling intra-bench roads as the composition of these two components reduces the number of decisions variables required in the stochastic mathematical program, while still providing multiple access strategies, as the sub-road network provides multiple ways of traversing each super-road.

Figure 2. Isometric view of a bench depicting checkpoints (spheres), sub-roads (grid of arrows) and a super-road (curved arrow).

2.4. Road and ramp generation

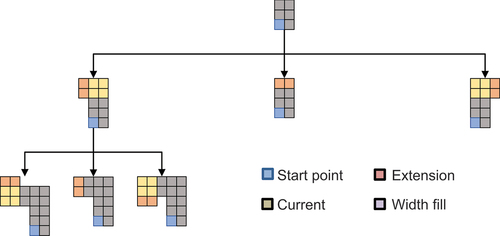
Automatic generation of both ramps, and intra-bench roads can be achieved using a graph traversal algorithm with unique stopping criteria to identify when a ramp/intra-bench road has been generated. Here, depth-first search (DFS) [26] is used as the traversal algorithm, which starts at a defined initial location and constructs a path by recursively adding/removing extensions to the current path at each recursive step. Extensions to the path are generated such that they maintain the desired path width and satisfy any operational constraints such as turning radius, length, complexity, etc. An example of automatic path generation through DFS is provided in Figure 3, where path extensions (orange) are added to the path, and fill blocks are inserted (yellow) as required to maintain path width.

Figure 3. Ramp and road generation tree. The children of each node compose the set of all possible roads that can be constructed by adding a single extension.

2.5. Definitions and notation

The tables in this section present the indices, sets, constants and variables used to define the proposed SIP. Table 1 presents the index notation, while Table 2 contains all sets of variables used throughout the formulation. Tables 3 and 4 present the constants and variables, respectively.

Table 1. Indices.

$\mathit{i}$	Mining block index
$\mathit{s}$	Simulation index
$\mathit{t}$	Period
$\mathit{d}$	Ramp design index
$\mathit{j}$	Check point index
$\mathit{k}$	Super-road index
$\mathit{l}$	Sub-road index
$\mathit{g}$	Super-road segment index

Table 2. Sets.

$\mathit{CPI}\left(\mathit{i}\right)$	Set of checkpoints with windows overlapping block $\mathit{i}$
$\mathit{AD}{J}^R\left(\mathit{k}\right)$	Set of ramps (described by their location $\mathit{i}$, and design $\mathit{d}$) which terminate adjacent to the beginning of super road $\mathit{k}$
$\mathit{PRED}\left(\mathit{i},\mathit{d}\right)$	Set of predecessor blocks for ramp located at $\mathit{i}$, with design $\mathit{d}$
$\mathit{XSEC}\left(\mathit{i},\mathit{d}\right)$	Set of ramps intersecting ramp at location $\mathit{i}$, with design $\mathit{d}$
$\mathit{SEG}\left(\mathit{k}\right)$	Set of segments composing super-road $\mathit{k}$
$\mathit{AD}{J}^{\mathit{s}-}\left(\mathit{g}\right)$	Set of sub-roads traversing super-road segment $\mathit{g}$
$\mathit{AD}{J}^{\mathit{s}+}\left(\mathit{j}\right)$	Set of super-roads adjacent to checkpoint $\mathit{j}$
S	Set of simulations
I	Set of mining blocks
T	Set of years
D	Set of ramp designs
K	Set of super-roads
L	Set of sub-roads
J	Set of checkpoints

Table 3. Constants.

$v_{i,s}^t$	Economic value of block $\mathit{i}$ in period $\mathit{t}$ for scenario $\mathit{s}$
$\mathit{r}{c}^t$	Cost of placing or removing a ramp in period $\mathit{t}$
$c_o^{t-,+}$	Penalty cost for deviating below $\left(-\right)$ or above $\left(+\right)$ ore target
$c_g^{t-,+}$	Penalty cost for deviating below $\left(-\right)$ or above $\left(+\right)$ metal target

Table 4. Variables.

$b_i^t$	Binary	Mine block $\mathit{i}$ period $\mathit{t}$
$r_i^{t,d}$	Binary	Ramp with design $\mathit{d}$ exists at $\mathit{i}$ period $\mathit{t}$
${\hat{r}}_{\mathit{i}}^{\mathit{td}}$	Binary	Ramp with design $\mathit{d}$ placed/removed at $\mathit{i}$ in period $\mathit{t}$
${\mathrm{c}\mathrm{p}}_j^t$	Binary	Checkpoint $\mathit{j}$ is active in period $\mathit{t}$
$s_k^{t+}$	Binary	Super-road $\mathit{k}\in \mathit{K}$ is active in period $\mathit{t}$
$s_l^{t-}$	Binary	Sub-road $\mathit{l}\in \mathit{L}$ is active in period $\mathit{t}$
$d_s^{to-},d_s^{to+}$	Continuous	Deviation below/above target for ore tonnage in scenario $\mathit{s}$ in period $\mathit{t}$
$d_s^{tg-},d_s^{tg+}$	Continuous	Deviation below/above target for grade in scenario $\mathit{s}$ in period $\mathit{t}$

2.6. Stochastic integer program

2.6.1. Objective function

The objective function, shown in Equation (1)(1) $\begin{array}{l}\mathit{max}\underset{\mathit{Part1}}{\underbrace{\frac{1}{\left|\mathit{S}\right|}{\displaystyle \sum _{\mathit{s}\in \mathit{S}}{\displaystyle \sum _{\mathit{i}\in \mathit{I}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}{b}_i^t}}}{v}_{i,s}^t}}-\underset{\mathit{Part2}}{\underbrace{{\displaystyle \sum _{\mathit{i}\in \mathit{I}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}{\displaystyle \sum _{\mathit{d}\subset \mathit{D}}\mathit{r}}}}{c}^t{\widehat{r}}_{\mathit{i}}^{\mathit{t},\mathit{d}}}}\\ \underset{\mathit{Part3}}{\underbrace{\frac{1}{\left|\mathit{S}\right|}{\displaystyle \sum _{\mathit{s}\in \mathit{S}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}(c_o^{t-}{d}_{s,o}^{t-}+c_o^{t+}{d}_{s,o}^{t+}+c_g^{t-}{d}_{s,g}^{t-}+c_g^{t+}{d}_{s,g}^{t+})}}}}\end{array}$(1) consists of three main parts. Part 1 maximises the discounted cumulative cash flow of the extraction sequence, Part 2 incurs the cost of placing and removing ramps over the life of the mine, and Part 3 penalises deviations from grade and ore tonnage targets. Part 1 and Part 3 are identical to the objective function described in Ramazan and Dimitrakopoulos [5] without stockpiling.

(1) $\begin{array}{l}\mathit{max}\underset{\mathit{Part1}}{\underbrace{\frac{1}{\left|\mathit{S}\right|}{\displaystyle \sum _{\mathit{s}\in \mathit{S}}{\displaystyle \sum _{\mathit{i}\in \mathit{I}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}{b}_i^t}}}{v}_{i,s}^t}}-\underset{\mathit{Part2}}{\underbrace{{\displaystyle \sum _{\mathit{i}\in \mathit{I}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}{\displaystyle \sum _{\mathit{d}\subset \mathit{D}}\mathit{r}}}}{c}^t{\widehat{r}}_{\mathit{i}}^{\mathit{t},\mathit{d}}}}\\ \underset{\mathit{Part3}}{\underbrace{\frac{1}{\left|\mathit{S}\right|}{\displaystyle \sum _{\mathit{s}\in \mathit{S}}{\displaystyle \sum _{\mathit{t}\in \mathit{T}}(c_o^{t-}{d}_{s,o}^{t-}+c_o^{t+}{d}_{s,o}^{t+}+c_g^{t-}{d}_{s,g}^{t-}+c_g^{t+}{d}_{s,g}^{t+})}}}}\end{array}$(1)

2.6.2. Constraints

The following sub-sections present the constraints of the stochastic mathematical program, which when combined ensure equipment access to scheduled mining blocks.

Ramp Placement/Removal Constraints: The ramp placement/removal constraints in Equations (2)(2) ${\hat{r}}_{\mathit{t}}^{\mathit{t},\mathit{d}}\ge r_i^{t,d}-r_i^{t-1,d}\mathrm{\forall i}\in \mathit{I},\mathit{t}\in \mathit{T},\mathit{d}\in \mathit{D}$(2) and (3(3) ${\hat{r}}_{\mathit{t}}^{\mathit{t},\mathit{d}}\ge r_i^{t-1,d}-r_i^{t,d}\mathrm{\forall i}\in \mathit{I},\mathit{t}\in \mathit{T},\mathit{d}\in \mathit{D}$(3) ) ensure ramp placement/removal variables are greater than zero whenever a ramp is placed or removed, storing the absolute value of $r_i^{t,d}-r_i^{t-1,d}$ in ${\hat{r}}_{\mathit{i}}^{\mathit{t},\mathit{d}}$, which incurs a cost in the objective function.

(2) ${\hat{r}}_{\mathit{t}}^{\mathit{t},\mathit{d}}\ge r_i^{t,d}-r_i^{t-1,d}\mathrm{\forall i}\in \mathit{I},\mathit{t}\in \mathit{T},\mathit{d}\in \mathit{D}$(2)

(3) ${\hat{r}}_{\mathit{t}}^{\mathit{t},\mathit{d}}\ge r_i^{t-1,d}-r_i^{t,d}\mathrm{\forall i}\in \mathit{I},\mathit{t}\in \mathit{T},\mathit{d}\in \mathit{D}$(3)

Checkpoint Accessibility Constraint: The checkpoint accessibility constraint in Equation (4)(4) $\begin{array}{c}{b}_i^t\le \sum _{\mathit{j}\in \mathrm{CPI}\left(i\right)}^{\mathit{\hspace{0.17em}}}{\mathrm{c}\mathrm{p}}_{\mathrm{j}}^{\mathrm{t}}\mathrm{\forall i}\in \mathit{I},\mathit{t}\in \mathit{T}\end{array}$(4) ensures that a block may only be mined if it is within the window of an active checkpoint. Since a block may be within the window of multiple checkpoints, the activation state of all intersecting checkpoints must be summed, which is achieved by summing over all $\mathit{c}{p}_j^t\mathrm{\forall j}\in \mathit{CPI}\left(\mathit{i}\right)$. 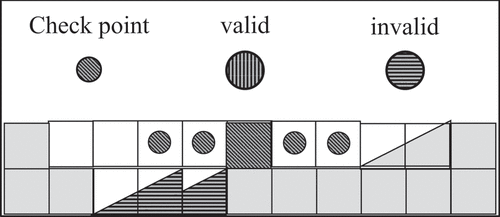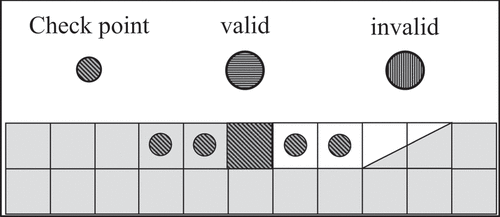Figure 4 shows a cross-section view of a bench with a ramp, checkpoint and accessible blocks, providing a visual representation of the constraint. The checkpoint represented by the hatched square has a window size of 5, providing access to all blocks annotated with hatched circles. Since the two blocks to the right of the checkpoint have already been mined, the only blocks available for mining are the two to the left of the checkpoint.

(4) $\begin{array}{c}{b}_i^t\le \sum _{\mathit{j}\in \mathrm{CPI}\left(i\right)}^{\mathit{\hspace{0.17em}}}{\mathrm{c}\mathrm{p}}_{\mathrm{j}}^{\mathrm{t}}\mathrm{\forall i}\in \mathit{I},\mathit{t}\in \mathit{T}\end{array}$(4)

Figure 4. Bench cross-section containing a ramp, checkpoint (hatched square), mined blocks (white), unmined blocks (shaded) and accessible blocks (hatched circles).

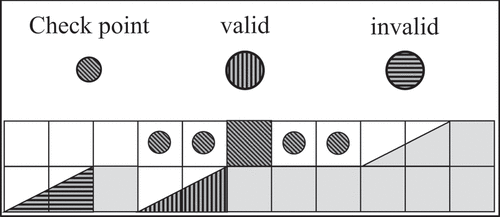
Ramp Location Accessibility Constraint: The ramp location accessibility constraint in Equation (5)(5) $\begin{array}{c}{r}_{i,d}^t\le \sum _{\mathit{j}\in \mathrm{CPI}\left(i^{-}\right)}^{\mathit{\hspace{0.17em}}}{\mathrm{c}\mathrm{p}}_j^t\mathrm{\forall }\mathit{i}\in \mathit{I},\mathit{t}\in \mathit{T},\mathit{d}\subset \mathit{D}\end{array}$(5) requires that ramps only be present where the start of the ramp is directly under an accessible location. By ensuring ramps are only placed under accessible blocks, a traversable road from the top of the pit to all ramps can be guaranteed in all periods. Since the start of a ramp may be under multiple checkpoint windows, the state of all checkpoints with windows intersecting the location directly above the start of the ramp ($i^{-})$ must be summed. In Figure 5, depicting the cross section of a bench, the vertically hatched ramp is valid because it starts directly below an accessible location, while the horizontally hatched ramp is invalid because it starts directly below a block that is not within the window of an active checkpoint.

(5) $\begin{array}{c}{r}_{i,d}^t\le \sum _{\mathit{j}\in \mathrm{CPI}\left(i^{-}\right)}^{\mathit{\hspace{0.17em}}}{\mathrm{c}\mathrm{p}}_j^t\mathrm{\forall }\mathit{i}\in \mathit{I},\mathit{t}\in \mathit{T},\mathit{d}\subset \mathit{D}\end{array}$(5)

Figure 5. Bench cross-section of accessible and inaccessible ramp placement. Vertically hatched ramp is accessible and horizontally hatched ramp is inaccessible.

Ramp Placement Constraint: The ramp placement constraint in Equation (6)(6) $\begin{array}{c}\sum _{\mathit{\tau }=1}^t\sum _{i^{\prime }\in \mathit{d}}{b}_{i^{\prime }}^{\mathit{\tau }}\le \left|\mathit{d}\right|\ast \left(1-r_{i,d}^t\right)\mathrm{\forall t}\in \mathit{T},\mathit{i}\in \mathit{I},\mathit{d}\subset \mathit{D}\\ \mathit{\hspace{0.17em}}\end{array}$(6) ensures that ramps are both placed in and underlain by solid material. This constraint is modelled by requiring all blocks associated with active ramps to be unmined by the period in which the ramp is present.

(6) $\begin{array}{c}\sum _{\mathit{\tau }=1}^t\sum _{i^{\prime }\in \mathit{d}}{b}_{i^{\prime }}^{\mathit{\tau }}\le \left|\mathit{d}\right|\ast \left(1-r_{i,d}^t\right)\mathrm{\forall t}\in \mathit{T},\mathit{i}\in \mathit{I},\mathit{d}\subset \mathit{D}\\ \mathit{\hspace{0.17em}}\end{array}$(6)

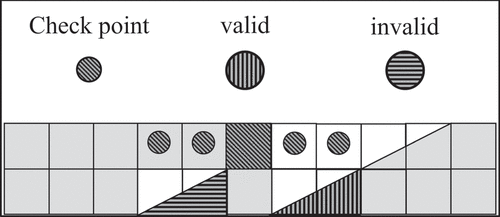
Ramp Predecessor Constraint: The ramp predecessor constraint in Equation (7)(7) $\begin{array}{c}\sum _{\mathit{\tau }=1}^t\sum _{i^{\ast }\in \mathrm{PRED}\left(\mathit{i},\mathit{d}\right)}{b}_{i^{\ast }}^{\mathit{\tau }}\ge \left|\mathrm{PRED}\left(\mathit{i},\mathit{d}\right)\right|\ast r_{i,d}^t\mathrm{\forall i}\in \mathit{I},\mathit{t}\in \mathit{T},\mathit{d}\subset \mathit{D}\end{array}$(7) ensures that ramps may only be present if their predecessors are mined. Since ramps contain multiple blocks, the predecessors of all blocks within the ramp must be mined to ensure that slope constraints are not violated. In the bench cross-section depicted in Figure 6, the vertically hatched ramp is valid because all blocks in its predecessor set are mined, while the horizontally hatched ramp is placed below unmined blocks making it invalid.

(7) $\begin{array}{c}\sum _{\mathit{\tau }=1}^t\sum _{i^{\ast }\in \mathrm{PRED}\left(\mathit{i},\mathit{d}\right)}{b}_{i^{\ast }}^{\mathit{\tau }}\ge \left|\mathrm{PRED}\left(\mathit{i},\mathit{d}\right)\right|\ast r_{i,d}^t\mathrm{\forall i}\in \mathit{I},\mathit{t}\in \mathit{T},\mathit{d}\subset \mathit{D}\end{array}$(7)

Figure 6. Bench cross-section of valid (vertically hatched) and invalid (horizontally hatched) ramp placements.

Ramp Intersection Constraint: The ramp intersection constraint in Equation (8)(8) $\begin{array}{c}\sum _{\left(i^{\ast },d^{\ast }\right)\in \mathrm{XSEC}\left(\mathit{i},\mathit{d}\right)}{r}_{i^{\ast },d^{\ast }}^{\mathit{t}}\le 1-r_{i,d}^t\mathrm{\forall t}\in \mathit{T},\mathit{i}\in \mathit{I},\mathit{d}\subset \mathit{D}\end{array}$(8) prevents two intersecting ramps from being present in the same period. In the bench cross-section shown in Figure 7, the placement of both ramps is invalid because they share a block, meaning they are intersecting.

(8) $\begin{array}{c}\sum _{\left(i^{\ast },d^{\ast }\right)\in \mathrm{XSEC}\left(\mathit{i},\mathit{d}\right)}{r}_{i^{\ast },d^{\ast }}^{\mathit{t}}\le 1-r_{i,d}^t\mathrm{\forall t}\in \mathit{T},\mathit{i}\in \mathit{I},\mathit{d}\subset \mathit{D}\end{array}$(8)

Figure 7. Bench cross-section with intersecting ramp placements.

Super-road Ramp Adjacency Constraint: The super-road ramp adjacency constraint in Equation (9)(9) $\begin{array}{c}\sum _{\left(\mathit{i},\mathit{d}\right)\in \mathrm{AD}{\mathrm{J}}^{\mathrm{R}}\left(\mathit{k}\right)}{r}_{i,d}^t\ge s_k^{t+}\mathrm{\forall }\mathit{t}\in \mathit{T},\mathit{k}\in \mathit{K}\end{array}$(9) ensures that all valid super-roads are adjacent to the end of a ramp, which is one of the three basic traversability requirements discussed above. To model this constraint, the variable associated with the super-road must be less than or equal to the sum of all ramp variables associated to ramps that terminate adjacent to the beginning of the super-road. In the bench cross-section presented in Figure 8, the solid super-road is valid because it begins adjacent to the end of a ramp, while the dashed super-road is invalid because no ramp terminates adjacent to the start of the road.

(9) $\begin{array}{c}\sum _{\left(\mathit{i},\mathit{d}\right)\in \mathrm{AD}{\mathrm{J}}^{\mathrm{R}}\left(\mathit{k}\right)}{r}_{i,d}^t\ge s_k^{t+}\mathrm{\forall }\mathit{t}\in \mathit{T},\mathit{k}\in \mathit{K}\end{array}$(9)

Figure 8. Bench cross-section with valid (solid) and invalid (dashed) super-roads.

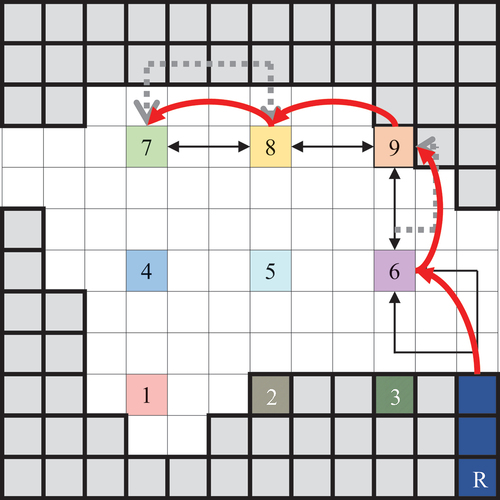
Active Sub-Road Constraint: The active sub-road constraint in Equation (10)(10) $\begin{array}{c}\sum _{\mathit{i}\in \mathit{l}}^{\mathit{\hspace{0.17em}}}\sum _{\mathit{\tau }=1}^t{b}_i^{\tau }-b_{i^{+}}^{\mathit{\tau }}\ge \left|\mathit{l}\right|\ast s_l^{t-}\mathrm{\forall l}\in \mathit{L},\mathit{t}\in \mathit{T}\end{array}$(10) ensures that active roads are unobstructed and underlain by solid material. This constraint can be formulated by summing the mining decisions for blocks in the path and subtracting mining decisions for blocks directly below the path. If the expression is equal to the length of the path, then the path must be unobstructed and underlain by solid material, meaning the road may be active. If the expression has a value less than the length of the path, it is either obstructed, not underlain by solid material, or both. In Figure 9, a plan view of a bench, containing a ramp, checkpoints and sub- and super-roads is depicted and serves as a visual aid for explanation of the following constraints. The sub-roads denoted by the solid black arrows are valid because they progress through mined blocks, and are entirely underlain by solid material; however, the dotted-grey sub-roads are invalid because they progress through unmined blocks.

Figure 9. Plan view of bench with a ramp (R), checkpoints (numbered blocks), sub-roads (straight) and super-roads (curved).

(10) $\begin{array}{c}\sum _{\mathit{i}\in \mathit{l}}^{\mathit{\hspace{0.17em}}}\sum _{\mathit{\tau }=1}^t{b}_i^{\tau }-b_{i^{+}}^{\mathit{\tau }}\ge \left|\mathit{l}\right|\ast s_l^{t-}\mathrm{\forall l}\in \mathit{L},\mathit{t}\in \mathit{T}\end{array}$(10)

Active Super-Road Constraint: The active super-road constraint in Equation (11)(11) $\sum _{\mathit{l}\in \mathit{AD}{\mathit{J}}^{\mathit{s}-}(\mathit{g})}{s}_l^{t-}\ge s_k^t\mathrm{\forall g}\in \mathit{SEG}(\mathit{k}),\mathit{t}\in \mathit{T},\mathit{k}\in \mathit{K}$(11) ensures that each segment of an active super-road is traversable by at least one active sub-road. The constraint can be formulated by ensuring that for each segment of the super-road, the super-road variable is less than or equal to the sum of active sub-roads traversing the segment. In the bench plan-view provided in Figure 9, the super-road denoted by the set of contiguous red arrows is valid because each segment (individual red arrow) of the super-road can be traversed by at-least one valid sub-road (black arrow).

(11) $\sum _{\mathit{l}\in \mathit{AD}{\mathit{J}}^{\mathit{s}-}(\mathit{g})}{s}_l^{t-}\ge s_k^t\mathrm{\forall g}\in \mathit{SEG}(\mathit{k}),\mathit{t}\in \mathit{T},\mathit{k}\in \mathit{K}$(11)

Active Checkpoint Constraint: The active checkpoint constraint in Equation (12)(12) $\begin{array}{c}\sum _{\mathit{k}\in \mathrm{AD}{\mathrm{J}}^{\mathrm{s}+}\left(\mathit{j}\right)}^{\mathit{\hspace{0.17em}}}{s}_k^{t+}\ge \mathit{c}{p}_j^t\mathrm{\forall }\mathit{j}\in \mathit{J},\mathit{t}\in \mathit{T}\end{array}$(12) ensures that checkpoints are only active in the periods in which they may be accessed through a valid haul road. The constraint is formulated by ensuring that the sum of all variables associated to super-roads that intersect that the checkpoint is greater than or equal to the variable associated to the checkpoint.

(12) $\begin{array}{c}\sum _{\mathit{k}\in \mathrm{AD}{\mathrm{J}}^{\mathrm{s}+}\left(\mathit{j}\right)}^{\mathit{\hspace{0.17em}}}{s}_k^{t+}\ge \mathit{c}{p}_j^t\mathrm{\forall }\mathit{j}\in \mathit{J},\mathit{t}\in \mathit{T}\end{array}$(12)

2.6.3. Complexity

The size of the models required to optimise the design of ramps, while ensuring feasible equipment access to every scheduled mining block grows quickly with the size of the block model. If the complexity of the model is inspected on a per bench basis, then on a bench with $\mathit{N}$ blocks, there are $\mathit{N}\cdot \left(\mathit{N}-1\right)$ possible ordered block pairings, each required to be connected by a set of intra-bench roads $R_S$. Meaning that on a per bench basis the number of binary decision variables required to model accessibility can be roughly described by $\mathit{N}\cdot \left(\mathit{N}-1\right)\ast \overline{\left|R_S\right|}$, where $\overline{\left|R_S\right|}$ is the average size of the intra-bench road sets. This complexity is problematic as both the number and size of the road sets $R_S$ grow exponentially quickly with the size of the bench.

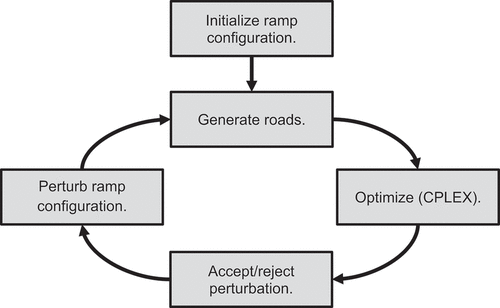
To solve the related SIP, the proposed method employs an iterative solution procedure, presented in Figure 10. The iterative solution procedure splits the entire problem into two components: a ramp configuration component, and a scheduling component. First, an incumbent ramp and road configuration is generated, containing only a small subset of ramps and roads that are to be included in the SIP, limiting the number of binary decision variables and constraints required to model accessibility. The SIP is then optimised using CPLEX, and the algorithm continues by perturbing the incumbent set of ramps and roads, reoptimising and accepting/rejecting the perturbation using the simulated annealing acceptance criteria [27].

Figure 10. Optimisation loop.

3. Case study

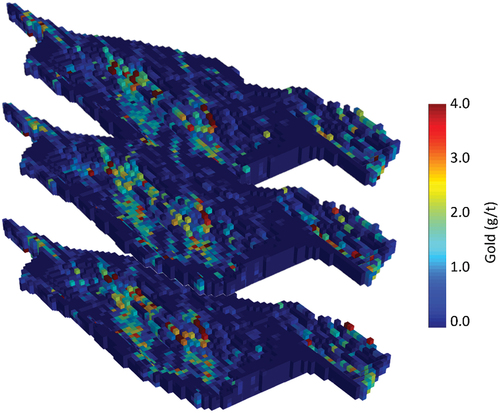
The method described above is applied to a gold deposit, consisting of a single mine and processor. The mine’s block-model contained 10, 500 blocks (10 m × 10 m × 10 m), with gold grade uncertainty described by 10 equiprobable geostatistical simulations, generated via high-order simulation [28], shown in Figure 11. The deposit was scheduled over a period of 7 years, with a mining capacity of 15 Mta and a processing capacity of 6 Mta.

Figure 11. Simulated realisations of gold grades (g/t).

Pre-processing of the block model resulted in the construction of 357 checkpoints, 1942 sub-roads and 2640 super-roads. The ramps were required to have a width of two blocks, and a centerline length of three blocks. The optimisation parameters are summarised in Table 5.

Table 5. Optimisation parameters.

Parameter	Value
Metal Price ($/oz)	1200
Recovery (%)	90%
Mining cost ($/t)	5
Processing cost ($/t)	15
Ramp placement/removal cost ($)	300,000

Cross sections of the schedule are provided in Figures 12 and 13, and snapshots of the scheduled blocks and placed ramps for periods 2, 4 and 7 are provided in Figure 14. Initially, all mining activity in year 2 and earlier is largely focused on the left side of the pit, providing space for ramp placement, and allowing early access to ore deeper in the mine. As the mine life progresses, much of the mining activity migrates to the right wall, where it is uniformly mined until the last period when ore in the bottom of the pit is cleaned up.

Figure 12. Cross-section at x = 39.

Figure 13. Cross-section at x = 52.

Figure 14. Plan view of the open pit denoting mined blocks (light colors) and ramps (dark blue) in years 2, 4 and 7.

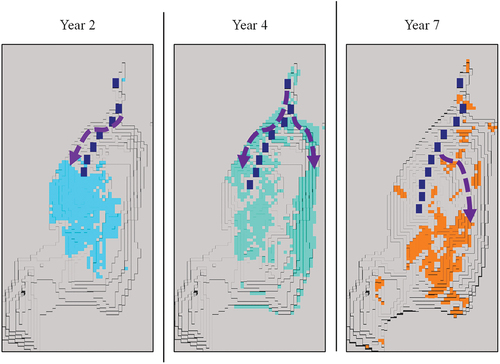
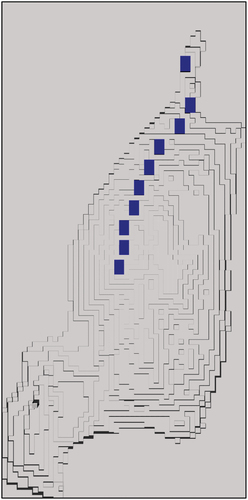
A plan view of the final ramp placement can be found in Figure 15 and shows that the ramp is placed against the left pit wall. Though several of the ramp segments could be pushed a few blocks tighter to the wall, the overall shape of the ramp closely follows the contour of the pit from crest to the floor. The left side of the pit is also significantly steeper than the right side of the pit, which may result from the blocks on the left side of the pit being closer to the ramp, requiring shorter access roads. Blocks on the right side of the pit are significantly further from the ramp, requiring longer roads, which are much easier than their shorter counterparts to invalidate. As a result, the blocks on the right side of the pit are much harder to access, and the optimiser may have been forced to leave unmined regions to ensure the scheduled blocks can be accessed through the provided roads.

Figure 15. Plan view of the open pit denoting final ramp placement (dark blue).

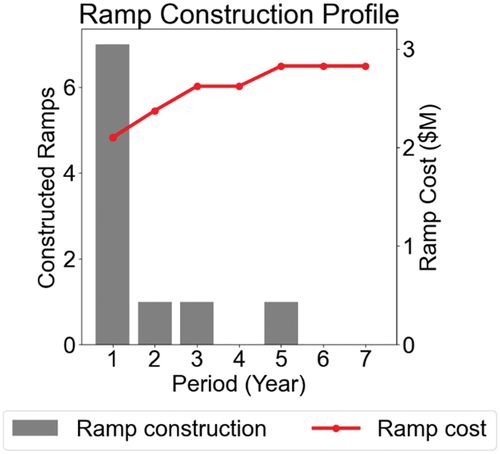
The schedule was forced to dig deep early to meet production targets, resulting in the placement of seven ramp segments in the first period, with only three ramp segments placed throughout the remainder of the schedule. The ramp placement profile over the life of mine, along with the cumulative ramp construction cost is provided in Figure 16. In total, ramp construction costs $2.8 million over the life of mine; however, this does not include the additional cost of stripping the required over burden to place the ramps.

Figure 16. Ramp placement profile and cumulative construction costs of optimised ramp design.

Though the SIP had the option to place multiple ramps on the same bench or remove previously placed ramps, it chose to never do so. Instead, the optimiser only placed one ramp per bench and left them untouched for the duration of the mine life. The singular ramp per bench strategy likely results from two causes: the ramp configuration provided poor quality options for additional ramps, or the schedule is unable to utilise the benefit provided by an additional ramp. In the first case, the additional ramp options may not provide earlier or more access to ore, meaning the optimiser only incurs the construction cost if the ramp is placed. In the second case, though the ramp may provide earlier or more access to ore, the schedule may be able to saturate production, with high-grade material using only one ramp, making the additional ramp redundant.

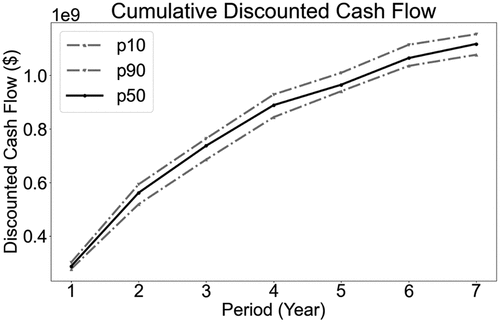
The cumulative discounted cash flow, including ramp construction cost, is provided in Figure 17. Over the life-of-mine, the schedule and ramp design achieve an NPV of $1.1 billion. Although the direct construction cost of the ramps is low, the total effect of ramps on the cash flow is significant as ramps control material availability, impacting when and where mining can happen in the pit. Ramps also require additional stripping of waste material, which incurs a cost, but also consume production capacity which may otherwise be used for ore.

Figure 17. Forecasted cumulative discounted cash flow of production schedule and ramp design.

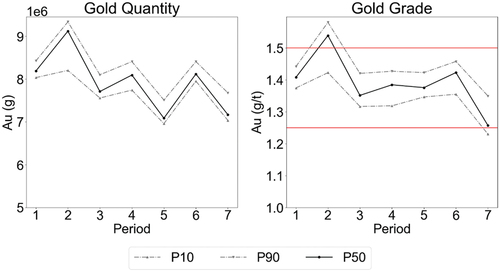
The gold production and average head grade over the life of mine are provided in Figure 18. Excluding year 2, where the schedule is likely to exceed the target grade ceiling, the head grade is maintained within its target range of 1.25 g/t−1.5 g/t. The corresponding gold production profile mimics the shape of head grade profile, with a peak production of 9 million grams in year 2, and 7–8 million grams in all other years. In the final year, even though the head grade is at its lowest, gold production is maintained relatively high due to the ore tonnage.

Figure 18. Forecasted gold quantity and grade of life-of-mine production schedule.

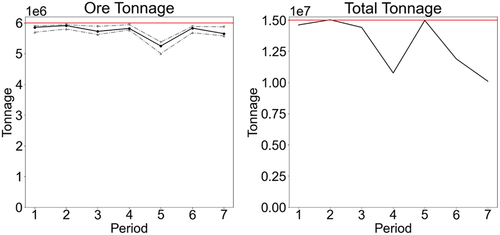
Figure 19 provides the ore tonnage and total tonnage profiles over the life-of-mine. Except for year 5, where a drop in production is observed, the ore production is maintained near the 6 Mta capacity limit. The corresponding total tonnage profile over the life of mine exhibits large variations in production. In years 1, 2, 3 and 5, production is at or near the 15 Mta limit, while in years 4, 6 and 7, production decreases to 11, 12 and 11 Mta, respectively.

Figure 19. Forecasted ore and total tonnages of production schedule.

4. Conclusions

An extension to the two-stage SIP proposed in Ramazan and Dimitrakopoulos [5] for jointly optimising long-term open-pit mine production schedules and ramp design while ensuring feasible equipment access was proposed. The method maximises the NPV of the production schedule and ramp design while ensuring feasible equipment access to scheduled mining blocks and managing the risk of not meeting production targets. The method requires a library of ramps and roads to be predefined, which can be automatically generated by the DFS algorithm presented. From the pre-defined library of ramps and roads, an optimal ramp design and schedule is generated, while ensuring equipment access through the selected ramps and provided roads.

The method was applied to a gold deposit, with gold grade represented by 10 geostatistical simulations, to develop a life of mine production schedule and ramp design. The optimised ramp design closely followed the contour of the pit on the left side and the associated optimised production schedule maintained gold grade within the target range, while satisfying processing and mining capacities. The results demonstrate the method's ability to jointly optimise the ramp design and schedule, producing a ramp design that provides access to desirable material in each period and an optimised schedule that utilises the material access provided by the ramp.

The joint stochastic optimisation of long-term open-pit mine production schedules and ramp design extends the formulation proposed in Ramazan and Dimitrakopoulos [5]. Future research in this direction should seek to incorporate this method into the simultaneous optimisation of mining complexes [15]. Additionally, the method only considers the construction cost of the ramps and not the associated haulage costs. Extending the method to incorporate haulage costs would enable better haul road design.

Acknowledgments

The work in this paper was funded by the National Sciences and Engineering Research Council (NSERC) of Canada CRD Grant 500414-16 and NSERC Discovery Grant 239019, the industry consortium members of McGill University’s COSMO Stochastic Mine Planning Laboratory (AngloGold Ashanti, BHP, De Beers, AngloAmerican, IAMGOLD, Kinross Gold, Newmont Mining, and Vale) and the Canada Research Chairs Program.

Disclosure statement

No potential conflict of interest was reported by the author(s).