Survival regression by data fusion

Abstract

Any knowledge discovery could in principal benefit from the fusion of directly or even indirectly related data sources. In this paper we explore whether data fusion by simultaneous matrix factorization could be adapted for survival regression. We propose a new method that jointly infers latent data factors from a number of heterogeneous data sets and estimates regression coefficients of a survival model. We have applied the method to CAMDA 2014 large-scale Cancer Genomes Challenge and modeled survival time as a function of gene, protein and miRNA expression data, and data on methylated and mutated regions. We find that both joint inference of data factors and regression coefficients and data fusion procedure are crucial for performance. Our approach is substantially more accurate than the baseline Aalen's additive model. Latent factors inferred by our approach could be mined further; for CAMDA challenge, we found that the most informative factors are related to known cancer processes.

Keywords:

• survival regression
• data fusion
• collective matrix factorization
• latent models
• cancer data

Introduction

Identification of driving events and their hazard rates for cancer progression remains a major challenge in cancer studies.¹ Recently, initiatives such as The Cancer Genome Atlas (TCGA)² and International Cancer Genome Consortium (ICGC)³ were launched to coordinate large-scale cancer genome studies across different cancer types and subtypes of clinical importance. They collect data that span patients, cancer types and diverse biological data types to address the richness of genomic and molecular mechanisms that play critical roles during cancer development. Importantly, these include data from matched tumor and non-tumor tissues.⁴ Rich, diverse, large and complex data sets generated within cancer genome projects now require computational methods that can collectively address them, provide interpretations on the genome-scale, and further integrate them with other genomic, clinical and functional information.

One of the fundamental goals of bioinformatic approaches in cancer studies is cancer subtype classification,^5-8 whereby a heterogeneous population of tumor samples is partitioned into biologically and clinically meaningful subtypes. Stratification of tumors is typically determined by the similarity of molecular profiles and correlated with clinical phenotypes including patient survival time and response to chemotherapy. Most current attempts to stratify tumors have used a single source of biological information and have derived molecular profiles from mRNA expression data,^8,9 somatic mutations^10,11 or methylation data.¹² They have discovered informative subtypes in diseases such as breast cancer and glioblastoma but have also reported a lack of correlation between derived profiles and clinical phenotypes in certain cancer types, including colorectal and lung tumors.^6,13 These shortcomings might be due to data incompleteness, noise inherent to biological measurements and limitations of data analysis methods.

Although individual data sets have long been used to stratify patients, stratification based on multiple types of data, such as expression, methylation and somatic mutation profiles, has been more challenging. These data sets are fundamentally different from each other, both in type and in structure. Somatic mutation profiles are extremely sparse and dispersed since typically only a small fraction of genes are mutated and patients diagnosed with the same cancer type share few, if any, mutations.¹⁴ On the other hand, methylation, miRNA expression and gene expression measurements assign quantitative values to nearly all markers, miRNAs and genes, respectively, in every patient. These data also naturally come at different levels of granularity and describe distinct biological data types, such as genes, proteins, miRNAs and methylation markers, among others. Heterogeneity of data generated by an increasing number of cancer studies hence limits the usage of naive computational approaches that either cannot be applied to such data or have to discard potentially beneficial biological information.

Here we report that the problems that stem from data diversity can be largely surmounted by data fusion, which can collectively consider a plethora of data sets coming from both directly and indirectly related data domains and provides gains in accuracy through data integration.¹⁵ We focus on the prediction of patient survival time and the identification of crucial clinical and molecular features. We propose a new machine learning approach that can consider a potentially large number of heterogeneous data sets to infer latent factors for a survival regression model. Its principal innovation is simultaneous inference of patient profiles and estimation of the influence of latent factors on patient survival time. Below we describe the key concepts behind the proposed approach and demonstrate its high predictive accuracy in 3 ICGC cancer studies.

Results and Discussion

Overview of data fusion for survival regression We here propose a method called DFMF-SR that couples Aalen's additive model for survival regression and matrix factorization-based data fusion into a joint inference procedure. The principal novelty of the approach is the establishment of interdependence between Aalen's time-varying regression coefficients and fused latent matrix factors during model inference. Intuitively, in each iteration of the algorithm, current estimates of patients' survival time influence the optimization of latent matrix factors and vice-versa. Figure 1 shows an exemplar data fusion graph of 8 data sets together with patient survival data and their corresponding latent matrix factors as inferred by DFMF-SR. We summarize relationships present in every data set ($${\mathit{R}}_{ij}$$) with a mapping from objects, i.e., the units of analysis, to sets of objects called latent factors (columns in $${\mathit{G}}_i$$ and $${\mathit{G}}_j$$) and pairwise relations between latent factors themselves ($${\mathit{S}}_{ij}$$). The inference process aims at identifying objects that are similar to each other in terms of their affiliation with latent factors. Similar objects are mapped to the same latent factor. Individual objects are allowed to instantiate similarity patterns with multiple latent factors.

Figure 1. Example illustrating survival regression by data fusion (DFMF-SR). The left pane shows the data fusion graph. Nodes in the fusion graph correspond to different types of objects considered by the system. Edges represent data matrices that describe relationships between objects of different types. For example, rows of matrix ("A," "E") correspond to objects "A" and columns agree with objects of type "E." A designated node "S" in the square box serves for the times of the events. Matrix ("A," "S") contains patient survival data. It is a binary matrix indicating the times when the respective objects of type "A" experienced the event. Type "A" most often corresponds to patients or tumor samples and hence ("A," "S") encodes the amount of time that has passed from primary diagnosis until a patient's death. DFMF-SR naturally interleaves collective matrix factorization with estimation of survival regression coefficients. The right pane shows the latent data model inferred by DFMF-SR. Each matrix with gray entries identifies a mapping from objects to their respective latent factors, which are stored in matrix columns. The number of matrices with blue entries is the same as the number of data sets; each one stores pairwise relations between latent factors as supported by the corresponding data set. The matrix with entries colored in different shades of red holds time-varying survival regression coefficients.

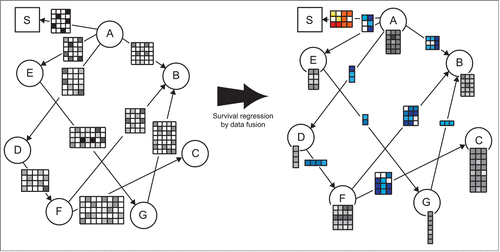
Overall, the goal of analysis with DFMF-SR is to identify the mapping of objects to a fixed number of latent factors, the pairwise relations among the factors, and regression coefficients of the survival model. The latter are optimized against good prediction of hazard rates using the mapping of individuals to latent factors. It should be noted that latent factors are inferred simultaneously for all objects and every object type in the system as shown in Figure 1. Figure 2 exposes the coupling between latent factors and survival coefficients that are estimated by regressing latent factors against patient survival data. Selection of a data set whose latent factors are used in survival model estimation is done prior to model inference. However, DFMF-SR is flexible in the sense that it allows one to consider for survival analysis the latent representation of any data set included in the system.

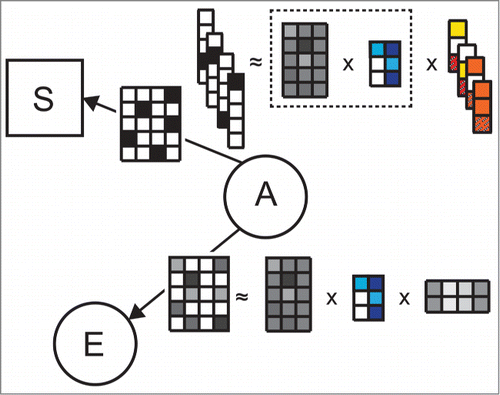
Figure 2. Example illustrating the use of latent factors from matrix tri-factorization for survival model estimation in DFMF-SR. Let us assume data matrix ("A," "E") was selected as a data set whose latent factors are used in the survival model. In each iteration of DFMF-SR, current tri-factorization of ("A," "E") is updated toward both better reconstruction of the matrix ("A," "E") and improved accuracy of the survival model. Parametrization of the survival model is given by vectors with red and orange entries. Since DFMF-SR builds upon Aalen's additive model, the number of vectors corresponds to the number of time points in the survival data. Each vector holds information about the importance of any latent factor for survival up to the respective time point. The dimensionality of each vector corresponds to the number of latent factors in ("A," "E"), i.e., the number of columns in the matrix with blue entries, plus one. An additional entry in each vector is reserved for the time-varying baseline hazard for survival.

Predictive performance

Table 1 reports the errors of predicting survival time for lung, kidney and head/neck cancer studies. We use protein expression and somatic mutation (p corresponds to samples, r to protein or to copy number somatic mutation; see sec. Factorized data fusion model for survival regression) data to regress against survival data. Our DFMF-SR approach (last row in Table 1) outperforms an alternative approach that does sequential survival regression by first transforming data into the latent space and then inferring a survival model independently of data transformation (second and third row in Table 1). Similar gains in accuracy of DFMF-SR are observed for other choices of r but are omitted here for brevity.

Table 1. Cross-validated error of predicted survival time. Latent data representations of protein expression values or somatic mutation data are regressed against patient survival data for 3 different cancer studies. We compare our approach (DFMF-SR) to a procedure, which first infers predictive factors by data fusion (DFMF in Step I) or principal component analysis (PCA in Step I) and then learns a regression model (Aalen in Step II). Aalen's regression modeling could be in principal applied to raw data (first row without feature construction in Step I), but fails due to high dimensionality of data sets

Approach		Protein expression			Somatic mutation
Step I	Step II	HNSC	KIRC	LUAD	HNSC	KIRC	LUAD
n. a.	Aalen	0.83	0.89	0.80	0.95	0.91	0.99
PCA	Aalen	0.73	0.70	0.69	0.71	0.73	0.72
DFMF	Aalen	0.67	0.65	0.66	0.61	0.68	0.61
DFMF-SR		0.56	0.62	0.59	0.54	0.58	0.53

Models inferred by DFMF-SR are also substantially better than Aalen's regression from the raw data (first line in Table 1). The less well-studied cancer data sets in CAMDA 2014 are challenging to analyze due to noisy measurements, missing data and high right censorship (given the available data). For example, 30% of tumor samples from the HNSC study do not have information about donors' last known vital status or time intervals since their primary diagnoses. Of the remaining samples, 86% belong to censored individuals. We observed that model performance crucially depends on the ability to infer latent space and reduce data dimensionality, and survival regression analysis fails to detect predictive signals if applied to high-dimensional untransformed data sets in the original data domain.

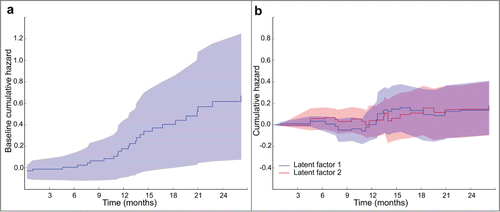
The additive regression model benefits from incorporating time into estimation of regression coefficients and can give information about effects of data features on patient survival time by plotting components of cumulative regression coefficients B*(t_k) against time. Figure 3 shows cumulative regression functions for 2 somatic mutation latent factors and the baseline regression coefficient in the HNSC cancer study. The baseline coefficient starts off small in the first 10 months after primary diagnosis and then increases (Fig. 3, right pane). Notice the different dynamics of regression coefficients for the 2 latent factors (Fig. 3, left pane). Gene sets belonging to these latent factors are enriched in biological processes known to play a role in the development of cancer,¹ such as regulation of nitric-oxide synthase activity, monooxygenase and oxidoreductase activity, nitric oxide processes, and cyclase activity (FDR < 4 × 10⁻⁴). This finding points to a possible utility of the proposed approach for uncovering critical factors and their changing influence across different stages of cancer progression.

Figure 3. Cumulative hazard plots produced by DFMF-SR showing (a) the cumulative hazards of selected somatic mutation latent factors, i.e., B*_i (t_k) of latent factor i for times t_k of the events, and (b) the baseline hazard in the HNSC cancer study. Notice that regression coefficients are the derivatives of the cumulative hazards and so it is the slopes of the plots that are informative.

Materials and Methods

We begin by briefly describing the Aalen's additive model for survival analysis and a recent approach to collective matrix factorization, which form the foundation of our work here. We then present our survival regression model that uses data fusion and latent factor parametrization, and conclude with an overview of considered data sets from the ICGC and a procedure for evaluation of predictive performance.

Background and preliminaries

Survival analysis and regression

Survival analysis studies the relationship between risk factors and a patient's time to the event (e.g. death, cancer relapse). The patient is referred to as right-censored if the event has not yet occurred by the end of the study. Traditional statistical techniques usually cannot be applied because of the skewness of the distribution of patient lifetime data, time-dependent features and data censoring. The survival probability until at least some time point is most often estimated with Kaplan-Meier statistics. When additional patient data are available, such as clinical covariates or information about somatic mutations that are present in the tumor, we can model time to the event through survival regression.

Aalen's additive model of survival regression

Aalen's additive model is an alternative to Cox's proportional hazards model.^16-18 It has time-varying regression coefficients, poses no assumptions about their parametric form and can provide information about the changing effects of data features on survival. Let λ(t) denote a vector of hazard rates for n individuals where λ_i(t) denotes the hazard rate of individual i. The additive model is given by λ(t) = X(t)β(t), where vector $\beta (t)\in {ℝ}^{m+1}$ holds the baseline hazard and ${\displaystyle m}$ regression coefficients that measure the influence of the respective features in $\mathit{X}\left(t\right)\in {ℝ}^{n\times \left(m+1\right)}$. The matrix X(t) is constructed as follows. If the ith individual is at risk at time t (the event has not yet occurred), then the corresponding row of X(t) contains the individual's feature profile, otherwise it is replaced with an all-zeros row. Aalen's model estimates cumulative regression coefficients defined by ${\displaystyle {\mathit{B}}_i\left(t\right)={\int }_0^t{\beta }_i\left(s\right)\text{d}s,i\in \left[m+1\right]}$. This is done by finding ${\mathit{B}}^{*}\left(t\right)=\sum _{t_k<t}\mathit{V}\left(t_k\right)I_k$, where ${\displaystyle t_k}$ are ordered times of events and ${\displaystyle I_k}$ is a binary vector indicating an individual who experiences the event at time ${\displaystyle t_k}$. The matrix ${\displaystyle \mathit{V}(t)}$ is computed by the least squares formula from ${\displaystyle \mathit{X}(t)}$.

Data fusion by matrix factorization (DFMF)

We have recently proposed a data fusion approach called DFMF¹⁵ (data fusion by matrix factorization) that can jointly factorize possibly many data matrices into low-dimensional matrix factors in a way that latent matrix factors are shared between factorizations of related data matrices. In DFMF, data matrices encode relations between 2 object types, say genes and gene ontology terms. Data matrices are related if they share an object type. An example of related matrices are the gene expression matrix and gene ontology term assignment matrix, as both matrices provide data on genes. DFMF can consider a set of data matrices. It can additionally consider constraints on the latent data representation that are expressed as matrices that relate objects of the same type, such as data on protein interactions. We have previously reported the utility of DFMF in functional genomics,¹⁵ inference on new diseases associations,¹⁹ and drug-induced liver injury prediction.²⁰ All these variants of data fusion assume the same factorization model, which is also used in our proposed extension of data fusion for survival regression.

Formally, let i and j denote 2 types of objects, such as genes and Gene Ontology terms, and let there be n_i objects of type ${\displaystyle i}$ and similarly n_j objects of type j. DFMF considers a collection $ℛ$ of relation matrices ${\mathit{R}}_{ij}\in {ℝ}^{n_i\times n_j}$, where R_ij encodes relations between objects of types i and j, and a collection   of constraint matrices ${\displaystyle {\Theta }_i^{\left(l\right)}}$ for ${\displaystyle l\in \left[l_i\right]}$, where ${\displaystyle {\Theta }_i^{\left(l\right)}}$ is ${\displaystyle l}$th constraint matrix for objects of type i. DFMF organizes data sets in a data fusion graph. An example of a data fusion graph is shown in Figure 4. The main component of DFMF is inference of latent matrix factors $${\mathit{G}}_i$$ (${\displaystyle {\mathit{G}}_i \ge 0}$) and $${\mathit{S}}_{ij}$$ by minimizing loss function $${\sum }_{{\mathit{R}}_{\mathit{i}j\in ℛ}}{\Vert {\mathit{R}}_{ij}-{\mathit{G}}_i{\mathit{S}}_{ij}{\mathit{G}}_j^T\Vert }_{\text{Fro}}^2+{\sum }_{{\Theta }_i\in \hspace{1em}}{\sum }_{l=1}^{l_i}\text{tr}({\mathit{G}}_i^T{\Theta }_i^{\left(l\right)}{\mathit{G}}_i)$$. In this way, every relation matrix $${\mathit{R}}_{ij}$$ is tri-factorized into ${\displaystyle {\mathit{G}}_i{\mathit{S}}_{ij}{\mathit{G}}_j^T}$ such that tri-factorization represents a good reconstruction of $${\mathit{R}}_{ij}$$, ${\mathit{R}}_{ij}\approx {\mathit{G}}_i{\mathit{S}}_{ij}{\mathit{G}}_j^T$, given the loss function of DFMF. Importantly, the inferred latent model contains both object type-specific latent matrix factors ($${\mathit{G}}_i$$) that are shared between decompositions of related data matrices and data set-specific matrix factors ($${\mathit{S}}_{ij}$$) that together constitute latent data representation and are used for prediction.

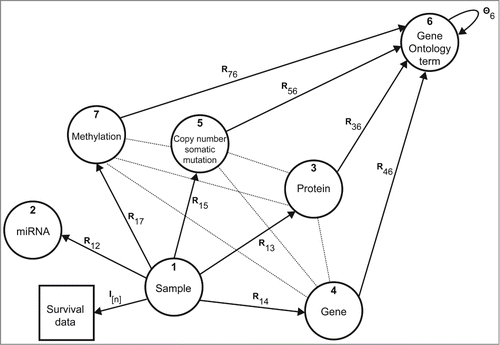
Figure 4. Data sources and their relations. Nodes in the graph correspond to different types of objects and edges denote data matrices R_ij or constraint matrices Θ_i. For example, matrix R₁₃ contains protein expression values, R₁₅ relates tissue samples to mutated genes in the tumor, and DNA methylation matrix R₁₇ reports on gene-based methylation Beta values of interrogated sites. Gene annotations from Gene Ontology are given in matrices R_x6, x ∈ {3, 4, 5, 7}. Constraint matrix Θ₆ encodes the semantic similarity of Gene Ontology terms as defined by the directed acyclic graph of the ontology.

Factorized data fusion model for survival regression

Solving the optimization problem

Following the notation introduced in the previous section and in Žitnik & Zupan (2015),¹⁵ DFMF-SR infers latent matrix factors ${\mathit{G}}_i$ (${\mathit{G}}_i \ge 0$) and ${\mathit{S}}_{ij}$ for all i and j, and cumulative regression coefficients B(t) for all time points of the events, $t_1<t_2<\cdots <{\mathit{t}}_{\mathit{n}}$, by minimizing the following objective function:(1) ${\displaystyle {\displaystyle \sum }_{{\mathit{R}}_{ij\in ℛ}}{\left|\left|{\mathit{R}}_{ij}-{\mathit{G}}_i{\mathit{S}}_{ij}{\mathit{G}}_j^T\right|\right|}_{\text{Fro}}^2+{\displaystyle \sum }_{{\Theta }_i\in \hspace{1em}}{\displaystyle \sum }_{l=1}^{l_i}\text{tr}\left({\mathit{G}}_i^T{\Theta }_i^{\left(l\right)}{\mathit{G}}_i\right)+{\displaystyle \sum }_{t_k<t_n}{\left|\left|I_k-{\mathit{G}}_p{\mathit{S}}_{pr}\left(t_k\right)\beta \left(t_k\right)\right|\right|}_{\text{Fro}}^2.}$(1)

Here, p and r are object types and specify data set whose fused latent representation we use to regress against survival data. The example in Figure 1 uses data set (“A,” “E”) to regress against survival data (“A,” “S”), hence in that example p corresponds to “A” and r to “E” (see also Fig. 2). The times t_k in Eq. (1)(1) ${\displaystyle {\displaystyle \sum }_{{\mathit{R}}_{ij\in ℛ}}{\left|\left|{\mathit{R}}_{ij}-{\mathit{G}}_i{\mathit{S}}_{ij}{\mathit{G}}_j^T\right|\right|}_{\text{Fro}}^2+{\displaystyle \sum }_{{\Theta }_i\in \hspace{1em}}{\displaystyle \sum }_{l=1}^{l_i}\text{tr}\left({\mathit{G}}_i^T{\Theta }_i^{\left(l\right)}{\mathit{G}}_i\right)+{\displaystyle \sum }_{t_k<t_n}{\left|\left|I_k-{\mathit{G}}_p{\mathit{S}}_{pr}\left(t_k\right)\beta \left(t_k\right)\right|\right|}_{\text{Fro}}^2.}$(1) are ordered times of the events and $I_k\in {ℝ}^{n_p}$ is a binary vector consisting of zeros except for a one in the position corresponding to an individual who experiences the event at time t_k. In our analysis, p refers to samples and r to features (e.g., protein expression profiles or mutated chromosomal regions).

We expand the objective function in Eq. (1)(1) ${\displaystyle {\displaystyle \sum }_{{\mathit{R}}_{ij\in ℛ}}{\left|\left|{\mathit{R}}_{ij}-{\mathit{G}}_i{\mathit{S}}_{ij}{\mathit{G}}_j^T\right|\right|}_{\text{Fro}}^2+{\displaystyle \sum }_{{\Theta }_i\in \hspace{1em}}{\displaystyle \sum }_{l=1}^{l_i}\text{tr}\left({\mathit{G}}_i^T{\Theta }_i^{\left(l\right)}{\mathit{G}}_i\right)+{\displaystyle \sum }_{t_k<t_n}{\left|\left|I_k-{\mathit{G}}_p{\mathit{S}}_{pr}\left(t_k\right)\beta \left(t_k\right)\right|\right|}_{\text{Fro}}^2.}$(1) using a trace operator similar to that in Žitnik & Zupan (2015)¹⁵ and derive iterative multiplicative update rules for the unknowns from the associated Lagrangian L. Derivatives of L with respect to $${\mathit{G}}_i$$ for ${\displaystyle i\ne p}$ remain the same as in Žitnik & Zupan (2015)¹⁵ and thus, their update rules are unchanged. The multiplicative update of latent matrix factor $${\mathit{G}}_p$$ (not shown here) follows from the following expression after some algebraic manipulation:${\displaystyle \begin{array}{l}\frac{\partial L}{\partial {\mathit{G}}_p}=2\sum _{j:{\mathit{R}}_{pj}\in ℛ}\left(-{\mathit{R}}_{pj}{\mathit{G}}_j{\mathit{S}}_{pj}^T+{\mathit{G}}_p{\mathit{S}}_{pj}{\mathit{G}}_j^T{\mathit{G}}_j{\mathit{S}}_{pj}^T\right)\\ +2\sum _{j:{\mathit{R}}_{jp}\in ℛ}\left(-{\mathit{R}}_{jp}^T{\mathit{G}}_j{\mathit{S}}_{jp}+{\mathit{G}}_p{\mathit{S}}_{jp}^T{\mathit{G}}_j^T{\mathit{G}}_j{\mathit{S}}_{jp}\right)\end{array}}$

${\displaystyle \begin{array}{l}+2\sum _{l=1}^{l_p}{\Theta }_p^{\left(l\right)}{\mathit{G}}_p\\ +2{\displaystyle \sum }_{t_k<t_n}(-I_k\beta \left(t_k\right){\mathit{S}}_{pr}^T+{\mathit{G}}_p\left(t_k\right){\mathit{S}}_{pr}\beta {\left(t_k\right)}^T\beta \left(t_k\right){\mathit{S}}_{pr}^T\{\backslash vscale200\%)-{\mathit{C}}_p,\end{array}}$where $${\mathit{C}}_p$$ is a constant factor. Similarly, update rules of latent matrix factors $${\mathit{S}}_{ij}$$ for ${\displaystyle i,j\ne p,r}$ are the same as those reported in Žitnik and Zupan (2015).¹⁵ The rule for $${\mathit{S}}_{pr}$$ is obtained from the associated partial derivative of the Lagrangian L given by:(2) ${\displaystyle \begin{array}{l}\frac{\partial L}{\partial {\mathit{S}}_{pr}}=-{\mathit{G}}_p^T{\mathit{R}}_{pr}{\mathit{G}}_r+2{\mathit{G}}_p^T{\mathit{G}}_p{\mathit{S}}_{pr}{\mathit{G}}_r^T{\mathit{G}}_r\\ -2{\displaystyle \sum }_{t_k<t_n}{\mathit{G}}_p{\left(t_k\right)}^T{I}_k\beta \left(t_k\right)+2{\displaystyle \sum }_{t_k<t_n}{\mathit{G}}_p{\left(t_k\right)}^T{\mathit{G}}_p\left(t_k\right){\mathit{S}}_{pr}\beta {\left(t_k\right)}^T\beta \left(t_k\right).\end{array}}$(2)

To properly formulate the multiplicative update rule $${\mathit{S}}_{pr}$$, one would need to solve a generalized linear matrix equation.^21-23 Such equations are difficult to analyze in their full generality, and necessary and sufficient conditions for the existence of their solutions are not known.²⁴ Also, current numerical techniques for solving generalized linear matrix equations are lacking or are not robust in large-scale settings.²⁴ We tackle this problem by randomly selecting a particular t_k in each iteration of the DFMF-SR algorithm and its associated term from the last component of the right side of Eq. (2)(2) ${\displaystyle \begin{array}{l}\frac{\partial L}{\partial {\mathit{S}}_{pr}}=-{\mathit{G}}_p^T{\mathit{R}}_{pr}{\mathit{G}}_r+2{\mathit{G}}_p^T{\mathit{G}}_p{\mathit{S}}_{pr}{\mathit{G}}_r^T{\mathit{G}}_r\\ -2{\displaystyle \sum }_{t_k<t_n}{\mathit{G}}_p{\left(t_k\right)}^T{I}_k\beta \left(t_k\right)+2{\displaystyle \sum }_{t_k<t_n}{\mathit{G}}_p{\left(t_k\right)}^T{\mathit{G}}_p\left(t_k\right){\mathit{S}}_{pr}\beta {\left(t_k\right)}^T\beta \left(t_k\right).\end{array}}$(2) . Based on this reduction we update $${\mathit{S}}_{pr}$$ by solving a Sylvester equation, a well-characterized type of linear matrix equation in which the coefficient matrices occur on both sides of the unknown matrix $${\mathit{S}}_{pr}$$.

Finally, Aalen's time-varying coefficients are computed in each iteration of DFMF-SR by regressing current estimates of $${\mathit{G}}_p$$$${\mathit{S}}_{pr}$$(t_k) for all t_k against lifetimes ordered by the times of the events with regularized least squares formulation (Fig. 2). The parameter selection and stopping criteria of the DFMF-SR algorithm are similar to those of the base DFMF algorithm.¹⁵

Determining assignment of objects to latent factors

DFMF-SR regresses against latent factors in $${\mathit{G}}_p$$$${\mathit{S}}_{pr}$$. Latent factor in $${\mathit{G}}_i$$, i.e., a particular column in $${\mathit{G}}_i$$, corresponds to a group of objects of type i. Since a latent factor does not directly represent any individual object, it is not readily interpretable in a biologically meaningful manner. To decipher the meaning of any latent factor, we wish to identify objects that are associated with it. By definition, the elements in $${\mathit{G}}_i$$ can only take nonnegative values and represent object membership strengths to latent factors. Membership strengths are nonnegative and real-valued due to the relaxation of orthogonality constraints on $${\mathit{G}}_i$$ in DFMF. Therefore, for a given latent factor c from $${\mathit{G}}_i$$, we can determine, which objects are most important and have the greatest membership to factor c. Specifically, object x of type i belongs to a factor c if ${\displaystyle c=arg\hspace{0.17em}ma{x}_{\tilde{c}} {\mathit{G}}_i\left(x,\tilde{c}\right).}$

Data and experimental setup

We consider large-scale cancer studies of 3 cancer types selected for the CAMDA 2014 Challenge in the 15.1 release of the International Cancer Genome Consortium (ICGC).³ These are head and neck squamous cell carcinoma (HNSC; 368 donors), kidney renal clear cell carcinoma (KIRC; 505 donors) and lung adenocarcinoma (LUAD; 461 donors). The ICGC provides data from matched tumor and non-tumor tissues. For each cancer type, data include protein, miRNA and normalized gene expression values, genome-wide information on the state of methylated fragments, somatic mutations and clinical annotation. We consider these data sets alongside Gene Ontology annotations, amounting to a total of 10 data sources (Fig. 4) for each cancer study. The base object type (p) is given by tumor samples that are associated with survival data based on the donor's last known vital status ("donor's vital status") and the interval from primary diagnosis to the last follow-up date in months ("donor's interval of last follow-up").

We evaluate the performance of survival models by leave-one-out cross-validation of tumor samples and score the models based on predicted survival times. We report transformed absolute error loss of survival time defined by ${\displaystyle l(y,\hat{\mathit{y}})=\left|log(y)-log({\hat{\mathit{y}}}_m)\right|}$, where ${\displaystyle {\hat{\mathit{y}}}_m}$ is the predicted median of survival time y. The median is the optimal predictor of the absolute error loss and is less affected by the long tails of survival distributions than the squared error loss. Log transformation addresses the concern that the absolute difference between predicted and actual survival time at a distant time point should result in smaller error than the same absolute difference achieved at a nearer time point.²⁵

Conclusion

Data fusion for survival regression is a new computational approach that predicts patient's survival time from a collection of heterogeneous data sets. The approach builds upon recently proposed collective matrix factorization¹⁵ and a well-known Aalen's additive model for survival regression.¹⁶ Unlike existing methods for survival time prediction, we formulated a joint inference procedure that allows us to simultaneously infer model parameters of collective matrix factorization and regression coefficients of Aalen's model. We demonstrated improved performance of our method over several baselines in case studies involving 3 cancer types from the International Cancer Genome Consortium and diverse data sets, such as gene and miRNA expression profiles, somatic mutation data, methylation and gene annotations from the Gene Ontology. Both latent data representation and joint inference, the 2 features of our approach, contribute substantially to accurate prediction of survival time. Our results allude to the potential benefits of data fusion when inferring survival models that are predictive of clinical outcomes.

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.

Funding

This work was supported by grants from the Slovenian Research Agency (P2–0209, J2–5480), EU FP7 (Health-F5–2010–242038), NIH (P01-HD39691) and the Fulbright Scholarship (B.Z.).