Analysis of linear feedback shift registers and chaos-based techniques for image encryption

ABSTRACT

Image encryption is not new. Several different encryption algorithms have been used. Some of the algorithms are based on random sequences generated using chao systems and DNA sequencing and others are based on compression. Still, others are based on Linear Feedback Shift Registers. This paper focuses on research solutions for securing digital images including medical images. Medical images are important and are generally regarded as sensitive in nature. In this research paper, higher order linear feedback shift registers are developed using combination of lower order LFSRs by suitable clocking and the ciphers generated are utilized to encrypt digital images. Our analysis involves using suitable metrics to compare the chaos-based and LFSR-based stream ciphers for image encryption.

KEYWORDS:

• Linear feedback shift registers
• encryption
• medical images
• ciphers
• chaos systems

1. Introduction

Data remains a critical component in information technology. Whether data is in motion or at rest, preserving it during transmission or in storage remains one of several challenges facing the information technology industry and business organizations. Business organizations both in the private and public sectors want assurances regarding the security of all organization’s owned critical data assets. In addition to data assets relating to organization’s products and services, businesses keep pertinent records of customers and clients. Business organizations want to be entrusted with the privacy of personal identifiable information of all customers and clients. Malicious attacks on information systems for managing data assets continue to be of major concern to many organizations. Organizations are saddled with security attacks on data assets that have serious impacts on investments and profitability.

Typically, data that is being transmitted via unsecured media need to be encrypted before transmission to render the information contained in data obfuscated. When an adversary accesses the resultant encrypted data, the adversary will be unable to recover or learn any information from the encrypted data. As a matter of convention, the encryption algorithm is publicly available. However, the encryption algorithm uses keystream that is secret and known only to the sender and the receiver. The receiver of the data must be able to recover the original data using a corresponding algorithm called decryption. The encryption and decryption algorithms are collectively called a cipher. A cipher is either symmetric (that is, it uses a single key called secret key) or asymmetric (uses two keys with one being a secret key called private key and the other called a public key). In the case of asymmetric cipher or public key cipher, the private key is only known to the receiver and the public key is widely distributed and readily available to anyone who wants to send data (or message) to the receiver. The sender encrypts data with a public key before sending to the receiver, who uses the private key to decrypt the encrypted data.

This paper focuses on the use of symmetric ciphers, particularly stream ciphers, for the encryption of digital images. While there is a variety of stream ciphers, the chaos-based and the linear feedback shift registers-based ciphers have gained significant momentum in the recent past years [1,2]. Both ciphers generate keystreams that are assumed to have significant levels of randomness.

2. Chaos-based ciphers

The chaos-based ciphers use chaotic maps obtained from simulations of dynamical systems using suitably chosen system parameters, see [3,4,5,12]. The values of chosen systems parameters become the secret key for the cipher. For example, a logistic map defined as $\mathit{f}\left(\mathit{x}\right)=\mathit{rx}\left(1-\mathit{x}\right)$ has $\left(\mathit{r},x_0\right)$ as the secret key. 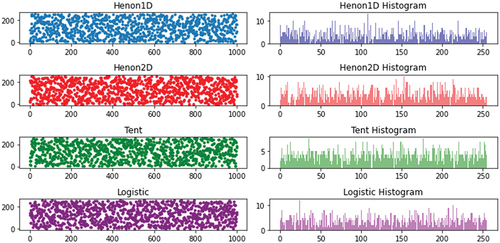The keystream that is used for the cipher is generated from the simulation: ${\left\{y_i\right\}}_1^{\mathit{N}}$, where $y_i=x_{\mathit{d}+\mathit{i}}=\mathit{f}\left(x_{\mathit{d}+\mathit{i}-1}\right).$ Here, the generated values ${\left\{x_i\right\}}_0^{\mathit{d}}$ are discarded. While this may not be necessary, it ensures an additional requirement for the secret key. For the paper, the following dynamical systems were used to generate chaotic maps:

1. Logistic: $\mathit{f}\left(\mathit{x}\right)=\mathit{rx}\left(1-\mathit{x}\right)$

2. Tent: $\mathit{f}\left(\mathit{x}\right)=\left\{\begin{array}{c}\mathit{rx},\mathit{x}<0.5\\ \mathit{rx}\left(1-\mathit{x}\right),\mathit{otherwise}\end{array}\right.$

3. One-Dimensional Henon (Henon1D): $\mathit{f}\left(\mathit{x}\right)=1-\mathit{a}{x}^2+\mathit{bx}$

4. Two-Dimensional Henon (Henon2D): $f_1\left(\mathit{x},\mathit{y}\right)=1-\mathit{a}{x}^2+\mathit{y},f_2\left(\mathit{x},\mathit{y}\right)=\mathit{bx}$

Although, there are a lot more sophisticated chaotic maps such as those based on Lorenz Systems for image encryption, the simulations for these listed maps do not require complicated operations such as numerical solutions of differential equations. Since our images are in the portable network graphics (PNG) file format and the type of PNG image, we used in this paper has four (4) colors in each pixel representing red, green, blue, and alpha (or transparency) channels. Since each color is 8-bit, each $y_i$ is converted to the equivalent of 8-bit integer using the formula $k_i=y_i\ast {10}^{16}\mathit{mod}\left(256\right)$. The values generated from each map after 1,000 iterations with $\mathit{d}=1,000$ are depicted in Figure 1.

Figure 1. Pseudorandom noise sequences generated from chaotic maps.

Eight (8) plots of pseudorandom noise (PN) sequences generated from four (4) chaotic maps (Henon1D, Henon2D, Tent and Logistic). The first two upper plots represent sequence from the Henon 1-dimensional map and the corresponding histogram profile. The next two plots represent sequence from Henon 2-dimensional map and the histogram profile. The next two plots represent the sequence from the Tent map and the corresponding histogram profile. The bottom two plots represent the sequence from logistic map and the corresponding histogram profile. In all plots, there was a considerable degree of randomness.

3. Linear feedback shift registers and proposed ciphers

A linear feedback shift register (LFSR) is fundamentally based on a linear array of D-type flip flops, see [6–10]. The flip flops are clocked to be in two stable states. As a finite state machine, flip flops have initial values which constitute the initial state of the LFSR. An LFSR of order n will have an initial state consisting of a sequence of bits, $s^0=\left\{s_0^0,s_1^0,s_2^0,\dots ,s_{n-1}^0\right\}$. Not all the flip-flops are clocked. A flip flop that is clocked has an output of 1 and the one that is not clocked has an output of 0. Generally, these values are called taps and they serve as connections for the input of the LFSR, i.e. they are used in calculating the input for the LFSR, hence the feedback mechanism. The output of an LFSR is usually the most significant bit of the LFSR bit sequence. Sequence states of the LFSR are obtained through a left or right shift of memory bit of one flip flop to the next. The way the input values are calculated for the LFSR is what gave rise to the two popular approaches, namely the Fibonacci and the Galois LFSR [8,9]. Let denote the values of the tap flip flops by the connection vector $\mathit{c}=\left\{c_0,c_1,c_2,\dots ,c_{\mathit{n}-1}\right\}$, the Fibonacci LFSR is defined by the following recurrence formula:

$s_i^k=s_{i+1}^{k-1}\mathit{and}{s}_{n-1}^k=\sum _{\mathit{j}=0}^{\mathit{n}-1}{c}_j{s}_j^{k-1}\mathit{mod}\left(2\right),\mathit{for}\mathit{i}=0,1,2,\dots ,\mathit{n}-2.$

In this case, the output of each flip flop contributes externally only to the input of the least significant bit, hence it is called external LFSR. The Galois LFSR is represented by

$s_i^k=c_{\mathit{i}+1}{s}_{i+1}^{k-1}\oplus s_0^{k-1}\mathit{and}{s}_{n-1}^k=c_0{s}_0^{k-1},\mathit{for}\mathit{i}=0,1,\dots ,\mathit{n}-2.$

The output contributes internally to the inputs of each flip flop; hence, it is called internal LFSR. While the two approaches will generate a pseudorandom noise (PN) sequence (not necessarily equal) starting with the same initial state vector, however, they will result in the same state vectors after ($2^n-1)$ clock cycles without counting the zero-state vector. For example, if $\mathit{n}=3,$ the number of possible state vectors is 7 not counting the zero state vector: $\left\{0,0,1\right\},\left\{0,1,0\right\},\left\{0,1,1\right\},\left\{1,0,0\right\},\left\{1,0,1\right\},\left\{1,1,0\right\},\left\{1,1,1\right\}.$ An LFSR is defined by its connection vector and the simulated LFSR will visit some if not all of these state vectors. A simulated LFSR that visits all the possible state vectors is called a maximum period LFSR. Maximum period LFSRs are used in this paper.

The output sequence using a single Fibonacci-based LFSR is

$\left\{s_0^0,s_0^1,s_0^2,\dots s_0^k,\dots \right\}=\left\{s_0,s_1,s_2,\dots ,s_{\mathit{n}-1},s_n,s_{\mathit{n}+1},s_{\mathit{n}+2},\dots .,\right\},$

where,

$s_{\mathit{n}+\mathit{j}}=c_o{s}_j+c_1{s}_{\mathit{j}+1}+c_2{s}_{\mathit{j}+2}+\cdot \cdot \cdot +c_{\mathit{n}-1}{s}_{\mathit{j}+\mathit{n}-1}\left(\mathit{mod}2\right),\mathit{forj}=0,1,2,\dots$

The way to obtain the d-bit sequence is to discard the first several bits of the output bit sequence and subsequently picking the next d consecutive bits. Let us define the d-bit sequence as

$\mathit{K}=\left(k_1,k_2,\dots ,k_d\right)$

and the bit pattern representation of an image (pixel) as

$\mathit{P}=\left(p_1,p_2,\dots ,p_d\right)$

The encrypted image (pixel) is obtained using XOR, thus,

$\mathit{C}=\left(c_1,c_2,\dots ,c_d\right),c_j=p_j\oplus k_j$

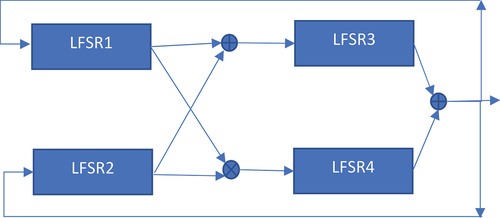
To decrypt the encrypted image, we would use: $p_j=c_j\oplus k_j.$ It is a common practice to combine LFSRs in a nonlinear fashion. Our proposed cipher combines four LFSRs of the same degree (we call it Simple Combined LFSR). The output of the first two LFSRs will be ORed and XORed to form the input of the remaining two LFSRs as shown in Figure 2. Although, we use LFSRs of the same order in this paper, it is, however, possible to use LFSRs of different orders; however, the algorithm must be modified so that the most significant registers of LFSR1 and LFSR2 are XORed with the corresponding $2^n$ when the output bit is 1.

Figure 2. Proposed LFSR cipher.

A diagram representing the proposed LFSR cipher. Four (4) LFSRs in all. The outputs of the LFSR1 and LFSR2 are XORed to form the input of the LFSR3 The outputs of the LFSR1 and LFSR2 are ANDed to form the input of LFSR4. The outputs of LFSR3 and LFSR4 are XORed to form the input of LFSR1 and LFSR2 (connected using arrow).

The following LFSR ciphers are tested in this paper.

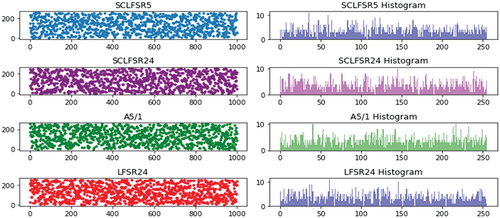
1. [SCLFSR5] Simple Combined LFSR Cipher with LFSRs defined as LFSR1(c = 37), LFSR2 (c = 41), LFSR3 (c = 47) and LFSR4 (c = 61) [SCLFSR5]. Each LFSR has a 5-bit state vector.

2. [A5/1] A5/1 Cipher with LFSRs defined as LFSR1 (c = 8388607), LFSR2 (c = 4194303), LFSR3 (c = 524287) with irregular clocking using registers 13 of LFSR1, 12 of LFSR2 and 11 of LFSR3. Just like SCLFSR5, the outputs from the three LFSRs are XORed for a 1-bit output. To have output like the original A5/1, we simulated 1000 times with regular clocking and another 1000 times with irregular clocking before generating the desired keystream.

3. [SCLFSR24] Simple Combined LFSR Cipher with LFSRs defined as LFSR1 (c = 16777243), LFSR2 (c = 28311553), LFSR3 (c = 16777351), and LFSR4 (c = 29491201). Each LFSR has a 24-bit state vector.

4. [LFSR24] A single LFSR (c = 29491291). This LFSR has a 24-bit state vector.

In a previous paper, the Python library for LFSRs and associated polynomials in Galois field were described [11]. The library has two classes, namely, Gf2Poly representing polynomials in Galois field and the LFSR representing linear feedback shift registers. The Gf2Poly class has an integer attribute that is used to represent the polynomial and the LFSR class has two attributes, one integer attribute representing the current state of the LFSR, and the second attribute is a Gf2Poly object representing the taps, the c value(s) in the parenthesis. The period of each LFSR of order 5 (i.e. a 5-bit LFSR) used in the SCLFSR was calculated to be $2^5-1=31.$ As demonstrated in Figure 3, single 5-bit LFSR would not be suitable for image encryption. There is clearly a pattern in the 1,000 PN sequences of size 8-bit as appose to the chosen 24-bit LFSR with a period of $2^{24}-1=16,777,215.$

Figure 3. PN sequences and histogram profiles.

Four plots of PN sequences generated from two LFSRs. The first LFSR is order 24 and the second LFSR is order 5. The upper two plots represent the sequence from order 24 LFSR and the corresponding histogram profile. These two plots demonstrate considerable randomness. The bottom two plots represent the sequence from order 5 LFSR and the histogram profile. These bottom plots show no degree of randomness.

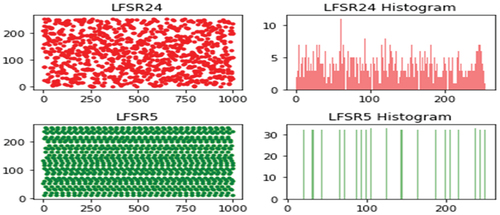
Like the chaotic maps, we computed the 1,000 PN sequences each of size 8-bit and Figure 4 presents the plots of the PN sequences and their histogram profiles.

Figure 4. LFSR-Based generated PN sequences and histogram profiles.

Eight plots of PN sequences from four (4) different LFSR-based ciphers and their histogram profiles. The ciphers are labelled SCLFSR5, SCLFSR24, A5/1 and LFSR24. The plots demonstrate a considerable level of randomness.

4. Image encryption and analysis

As indicated previously, a digital image (png) consists of 4-value pixels arranged in M rows and N columns. In the case where a pixel has less than 4 values, the algorithm must be modified accordingly. The encryption is done in two steps once the pixel values of the image have been determined. In the first step, we generate PN-sequence of size 4N using the appropriate cipher and encrypt each image row with the generated PN-sequence. This is called row wise encryption. The second step involves generating a second PN-sequence of size 4 M and encrypting the encrypted image from the first step with the second generated PN-sequence. Denote the 4M by 4N pixel values by IMAGE(I,J) and the 4N PN-sequence by ROW(I) and the 4 M PN-sequence by COL(J), the encrypted image, denoted by CIMAGE(I,J) is obtained using:

$\mathit{CMAGE}\left(\mathit{I},\mathit{J}\right)=\mathit{IMAGE}\left(\mathit{I},\mathit{J}\right)\oplus \mathit{ROW}\left(\mathit{I}\right)\oplus \mathit{COL}\left(\mathit{J}\right),\mathit{I}=1,\dots ,4\mathit{M},\mathit{J}=1\dots 4\mathit{N}$

The symbol ⊕ stands for exclusive OR operator. The PN sequences ROM(I) and COL(J) are generated using different initial parameters for both the chaos and linear feedback shift register ciphers. Note that the final state values of the simulation generating ROW(I) are used as the initial state values for the simulation generating COL(J).

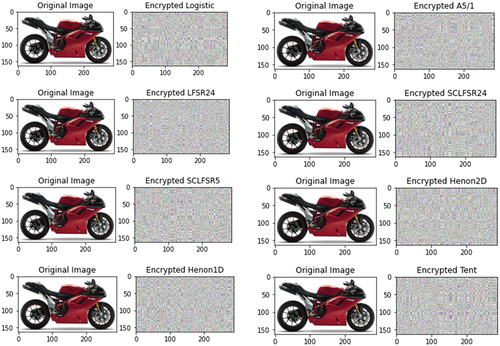
The encrypted images generated by all eight ciphers are shown in Figure 5.

Figure 5. Encrypted images by LFSR-Based and chaotic maps ciphers.

Eight plots of the original and encrypted images of a motorcycle using eight (8) different encryption algorithms, namely Logistic, A5/1, LFSR24, SCLFSR24, SCLFSR5, Henon2D, Henon1D, and Tent. The encrypted images from all eight ciphers have considerable degree of randomness, one cannot infer the original image from the encrypted one, unless through corresponding decryption algorithm with an appropriate key.

The two popular metrics for measuring the security strength of image encryption algorithms are the unified average changing intensity (UACI) and number of pixels change rate (NPCR) which are defined as

$\mathit{UAC}{I}_c=\frac{100}{255\mathit{MN}}\sum _{\mathit{i}=1}^M\sum _{\mathit{j}=1}^N|(\mathit{pIm}{g}_{ij}^c-\mathit{eIm}{g}_{ij}^c)|$

$\mathit{NPC}{R}_c=\frac{100}{\mathit{MN}}\sum _{\mathit{i}=1}^M\sum _{\mathit{j}=1}^N\mathit{f}\left(\mathit{pIm}{g}_{ij}^c,\mathit{eIm}{g}_{ij}^c\right),\mathit{where}\mathit{f}\left(\mathit{x},\mathit{y}\right)=\left\{\begin{array}{c}1,\mathit{x}!=\mathit{y}\\ 0,\mathit{x}=\mathit{y}\end{array}\right.$

Here, $\mathit{pIm}{g}_{ij}^c$ is the color value of pixel in the i-th row and j-th column of the original image and $\mathit{eIm}{g}_{ij}^c$ is the color value of pixel in the i-th row and j-th column of the encrypted image. These two metrics measure the sensitivity of the encryption algorithm when there is a small change in the original image, see [5,12]. These numbers determine the difficulty of the encryption algorithms to differential attacks. The NPCR and UACI values for all tested ciphers as shown in Table 1 are indications of their sensitivity to small changes in the pixel of the original image. The NPCR values for all algorithms are greater than 99% and UACI values are greater than 40%.

Table 1. Calculated NPCR and UACI Values.

	NPCR				UACI
	Color 1	Color 2	Color 3	Color 4	Color 1	Color 2	Color 3	Color 4
Logistic	99.59	99.64	99.59	99.56	40.68	43.01	41.99	48.05
Henon1D	99.57	99.57	99.55	99.52	40.26	43.05	42.07	47.99
Henon2D	99.59	99.65	99.6	99.58	40.45	43.16	41.8	47.98
Tent	99.62	99.61	99.6	99.62	40.24	42.98	42.09	48.08
LFSR24	99.68	99.59	99.62	99.64	40.16	42.89	42.09	47.98
SCLFSR5	99.66	99.64	99.59	99.63	40.35	42.97	42.14	47.9
SCLFSR24	99.58	99.61	99.64	99.6	40.08	43.07	42.01	47.89
A5/1	99.63	99.59	99.55	99.57	40.39	43.07	42.06	47.74

5. Conclusions

In this paper, the chaos-based ciphers were compared with linear feedback shift registers-based ciphers. Except for the A5/1 ciphers, all LFSR-based ciphers are new and are still being developed. While the theoretical randomness properties are currently being studied and will be reported in a different paper, the histogram profiles of the keystream sequences generated from all ciphers show randomness at best. One cannot infer any meaningful information from the encrypted images and the computed NPCR and UACI further indicate the strength of the ciphers from differential attacks.

Acknowledgments

This paper is partly supported by the National Science Foundation through the Excellence in Research (EiR) Program, Award #CNS 23000239.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

The work was supported by the National Science Foundation [CNS23000239].