Thomas Simpson and Dido’s problem

Abstract

An elegant geometrical argument concerning Dido’s problem, traditionally credited to Jakob Steiner in about 1840, appears to have been invented by Thomas Simpson, almost 100 years earlier. The argument itself uses only the idea of triangle area and the converse of Thales’ theorem about the angle in a semicircle. It appears in Simpson’s book Elements of Geometry, published in 1760, as part of a highly original section on ‘The Maxima and Minima of Geometrical Quantities’, but traces of the argument can even be found in an earlier edition dated 1747.

1. Introduction

This paper is concerned with the origin of an elegant and purely geometric approach to Dido’s problem.

According to legend, Queen Dido arrived at the North African coast in about 800 BCE and was granted as much land as she could encompass with an ox-hide. With great cunning, she cut the hide into very thin strips, and sewed them all together to make one long strip.

In its simplest and most well-known form, then, with a straight coastline, Dido’s problem becomes

Find the curve of given length which encloses maximum area when its ends lie on a given straight line.

Isoperimetric problems of this general kind have a long history, dating back to ancient Greece. They have also had a major influence on the development of modern mathematics (Bandle 2017), and are often very challenging.

Yet, in the case of Dido’s problem, and on the assumption that a solution actually exists, there is a delightfully simple way of proceeding … .

2. The geometrical argument

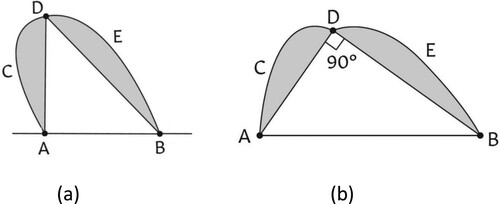
Suppose that we have found the curve of given length (ACDEB in Figure 1(a)) which, together with the given straight line, maximizes the enclosed area. And suppose, too, that there is some point D on the curve such that the angle ADB is not 90 degrees. Then, by adjusting the distance between the end points A and B until angle ADB is a right angle, while keeping the segments ACDA and BEDB fixed in both size and shape, we can keep the length of the curve ACDEB constant, yet increase the triangular area (Figure 1(b)). (For if we take, say, AD as the triangle’s base, then the triangle’s area will be greatest when its height is a maximum.)

Figure 1. The heart of the argument

But this would also increase the total area enclosed, contradicting our original assumption, which must therefore be false. So, all points D of the maximizing curve must subtend an angle of 90 degrees with its end points A and B.

It then follows that the maximizing curve must be a semicircle with AB as diameter, by appeal to the converse of Thales’s famous theorem. (Thales’s theorem itself says that if D lies on the semicircle with AB as diameter, then angle ADB is 90 degrees.)

3. Who invented it?

The elegant argument above seems to be universally credited to the great Swiss geometer Jakob Steiner (1796–1863), both in the research literature and in more ‘semi-popular’ accounts (see, e.g. Courant and Robbins 1941; Niven 1981; Hildebrandt and Tromba 1996).

In a paper of 1841, Steiner actually tackles the problem of proving that a closed plane curve of given length encloses maximum area when it is a circle. But in the first of five approaches to that problem, he quickly reduces it to Dido’s problem, and then employs precisely the argument above (Steiner 1841; Blasjo 2005).

Yet, while researching a recent book on geometry (Acheson 2020), I stumbled across what appears to be the very same line of reasoning in the textbook Elements of Geometry by Thomas Simpson, dated 1760 (Figure 2).

Figure 2. (left) Thomas Simpson (1710–1761) (right) Simpson’s Elements of Geometry, 1760.

Simpson’s book is, of course, influenced by Euclid’s Elements, but he frequently goes his own way, as is apparent from the forthright preface to a smaller, first edition, published 13 years earlier under a slightly different title (Simpson 1747):

My Design, in this little Book, is to lay, before the young Beginner, an easy Method for acquiring a competent Knowledge in the Subject of Geometry, without … being obliged to go through a Number of useless and tedious Propositions … .

This independence of spirit is perhaps hardly surprising, for while Simpson was a Fellow of the Royal Society, he was self-taught in mathematics and had little formal education (O’Connor and Robertson 2005; Blanco 2014).

In any event, Dido’s problem appears in the much-expanded 1760 edition of his book, as Theorem XIV in a highly unusual section called ‘Of the Maxima and Minima of Geometrical Quantities’. Simpson’s treatment of the problem is reproduced in full in Figure 3.

Figure 3. Theorem XIV from Simpson’s Elements of Geometry of 1760.

It could perhaps be argued that his diagram leaves something to be desired, because the two figures look identical, in contrast to Figure 1. So far as I can determine, however, the argument itself in Figure 3 is exactly the same as the one just presented and usually attributed to Steiner.

In particular, Simpson’s appeal to ‘Theorem 4’ in the fourth line of the second page is precisely to the idea that a triangle with two sides of given length has its greatest area when the two sides in question are at right angles.

And, three lines later, the phrase ‘which is repugnant’ marks Simpson’s arrival at the desired contradiction.

The only slight blemish is in the Corollary at the end. For Simpson appeals there to Theorem 13 of his Book 3, and this is without doubt, and as his prose rather suggests, Thales’s theorem itself, rather than its converse.

This surely detracts little, however, from a most elegant argument, traces of which can even be found in Simpson’s first edition of 1747, albeit with a polygonal boundary rather than one involving a smooth curve.

Disclosure statement

No potential conflict of interest was reported by the author(s).