Generation of almost rectangular, square, and hexagonal two-dimensional supercells

ABSTRACT

This study outlines procedures to make 2D supercells, of arbitrary crystals and orientations, with a given size and are almost commensurate with rectanglar, square, or hexagonal lattices. Quantitative measures on the commensurateness, or alikeness, are proposed. The outlined algorithms would be useful in defect calculations, including desorption and absorption, and generation of approximate 2D coincidence site lattices for epitaxial interface models with small lattice mismatch.

GRAPHICAL ABSTRACT

IMPACT STATEMENT

Quantitative measures on how commensurate a 2D unit cell is with a rectangular, square, or hexagonal lattice are proposed together with procedures to make an almost rectangular, square, or hexagonal supercell of an arbitrary crystal.

KEYWORDS:

• 2D supercell
• almost rectangular
• almost square
• almost hexagonal
• basis vectors
• algorithm

1. Introduction

Computational methods, such as first-principles calculations, to study reactions at the atomic scale level typically employ supercells of the surface. ZrO₂ exhibits catalytic behavior as it has both acidic and basic properties as well as both oxidizing and reducing properties [1]. ZrO₂ interacts with molecules including CO, H₂, CH₄, CO₂, H₂O, and hydrocarbons, opening up many possibilities of catalytic reactions [2]. In particular, interactions between monoclinic ZrO₂ (baddeleyite), which is the stable phase at room temperature, and CO [3] as well as OH groups [4,5] are studied extensively. On the other hand, TiO₂ has numerous applications [6] including photocatalytic water splitting and hydrogen production [7], photoelectrochemistry [8], dye sensitization and solar energy conversion, and photochemical air and water treatments. There are two major phases of TiO₂, rutile and anatase, and the latter is considered to be a better photocatalyst [9,10]. Interaction of the anatase TiO₂ (101) surface with water is extensively studied because most applications of TiO₂ involve an aqueous environment [11–13]. Additionally, adsorption of a monolayer of rutile and anatase TiO₂ was adsorbed on GaAs for use as a solar cell [14].

Epitaxial growth of a thin film on a substrate has many applications. A classical system is Cu (111) on α-Al₂O₃ (sapphire) (0001) reported by Katz in 1968 [15], which is a model system for epitaxy, adhesion, and other properties of metal-ceramic interfaces. Two distinct in-plane orientation relationships (ORs) are known, which are OR I, Cu < 110>//Al₂O₃ <10$\bar{1}$0>, and OR II, Cu < 110>//Al₂O₃ <2$\bar{1}$$\bar{1}$0> [16,17]. Katz reported OR I. Cu film up to 150 nm thick can be grown on Si with the OR Cu(001) [100]//Si(001) [110] [18]. The wurtzite structure semiconductor GaN is a widely used wide-gap semiconductor with applications for blue, violet, and ultraviolet light emitting devices, and a key technology is obtaining high-quality films through epitaxial growth on a sapphire substate [19,20]. The observed OR between GaN and sapphire is GaN (0001)//Al₂O₃ (0001) and GaN < 1$\bar{1}$00>//Al₂O₃ <11$\bar{2}$0> when the substrate is nitrided prior to growth, and GaN (3302) (sic)//Al₂O₃ (0001), GaN < 11$\bar{2}$0>//Al₂O₃ <1$\bar{1}$00>, and GaN < 1$\bar{1}$03>//Al₂O₃ <11$\bar{2}$0> for growth on a bare substrate. The [0001] directions of GaN and Al₂O₃ form a tilt angle of about 19° in the latter [21]. The two-dimensional (2D) semiconductor MoS₂ has a sulfur terminated edge direction of <11$\bar{2}$0> and can be epitaxially grown on SrTiO₃ with the following ORs: MoS₂ (0001)<2$\bar{1}$$\bar{1}$0>//SrTiO₃ (111)<1$\bar{1}$0>, MoS₂ (0001)<2$\bar{1}$$\bar{1}$0>//SrTiO₃ (110)<1$\bar{1}$0>, MoS₂ (0001)<2$\bar{1}$$\bar{1}$0>//SrTiO₃ (110)<1$\bar{1}$$\bar{2}$>, and MoS₂ (0001)<11$\bar{2}$0>//SrTiO₃ (001)<1$\bar{1}$0> [22]. Anatase TiO₂ can be grown on perovskite structure oxides as TiO₂ (001)[100]//SrTiO₃ (001)[100] [23] and TiO₂ (001)[100]//LaTiO₃ (001)[100] [24]. The electric and magneto-transport properties were measured on Nd-doped wurtzite structure ZnO grown epitaxially on MgO (100) [25]. This study reported the following ORs (the following indices are as reported in the reference although, for example, [110] is not in the (100) plane): ZnO [100]//MgO [110] and ZnO [210]//MgO [110] for wurtzite ZnO (001)//MgO (100) and ZnO [001]//MgO [410] and ZnO [100]//MgO [$\bar{1}$40] for wurtzite ZnO (100)//MgO (100). Most of the grain boundary planes mentioned here have square or hexagonal lattices,

Matthews and Blakeslee gave the critical thickness h_c of a strained thin film as $p{h}_c=\frac{p{h}_c}{qf}\left[\mathrm{l}\mathrm{n}\left(\frac{p{h}_{\mathrm{c}}}{b}\right)\right]+1$ based on mechanical equilibrium theory, where b is the length of the Burgers vector and f is the lattice misfit. The coefficients are p = 4 for a single epitaxial film on a substrate of infinite thickness and $q=2\pi \left(1+v\right)cos\lambda /\left(1-v^2{cos}^2\alpha \right)$, where $v$ is the Poisson ratio, $\alpha$ is the angle between the dislocation line and its Burgers vector, and $\lambda$ is the angle between the slip direction and the direction in the film plane perpendicular to the line of intersection of the slip plane and the interface [26]. The solution is given using Lambert’s W function as $\frac{h_c}{b}=\frac{-1}{fpq}W\left(\frac{-fq}{e}\right)$, where e is Napier’s constant. The normalized critical thickness (h_c/b) for 0.1, 0.2, 0.5, 1, 2, and 5% lattice misfits for an edge dislocation ($cos\alpha =0$) and $v=1/3$ are 234, 105, 36, 15, 6.3, and 1.8 monolayers, respectively [27]. Defects such as dislocations therefore exist in epitaxial interfaces except in very thin films with a very small lattice mismatch.

Determination of how the two crystals at the interface slide against each other, which is the rigid body translation (RBT) in grain boundary jargon, is another topic. Hinuma et al. suggested that the two surfaces at an interface might position themselves to maximalize overlap between the reaction fronts of each surface, which is where the charge density is near a certain value. This is a very bold approximation assuming that the bonding at an interface between two crystals can be estimated from the charge densities at their surfaces, but is still reasonable in some systems [28,29]. The number of RBT choices that need to be sampled becomes very limited in interfaces where the 2D primitive cells of the two crystals are relatively small but the interface must be described with a relatively large 2D primitive cell [30].

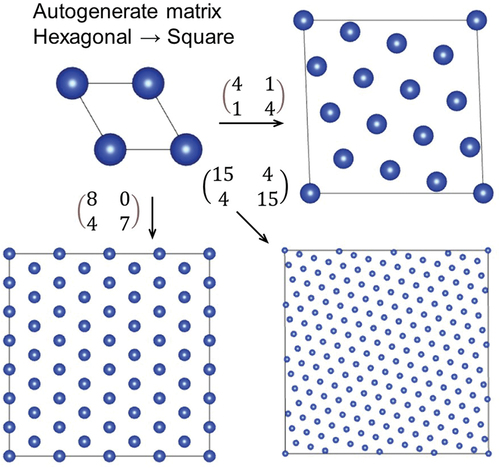
This study provides algorithms to find the following 2D supercells for further analysis:

1. Almost rectangular n-supercells when n is given. No limitation is imposed on the aspect ratio.

2. Almost square n-supercells when n is given. The aspect ratio should be as close to 1 as possible, which results in very few choices compared to almost rectangular supercells.

3. Almost hexagonal n-supercells when n is given. Again, the limitation on the aspect ratio results in very few choices.

4. Almost square supercells with basis vectors shorter than a given length. For each allowed basis vector, a counterpart basis vector that results in a supercell most alike to a square is identified.

5. Almost hexagonal supercells with basis vectors within a given length, which are obtained similarly to (D).

Applications of the algorithms include assistance in making supercells for adsorption/desorption analysis as well as interface models. Supercells where the surface is expressed as rectangular lattices are convenient to handle. Making H × K × 1 supercells are straightforward, but other choices with a more rectangular shape allow intuitional transformation between fractional and Cartesian coordinates of atoms. The distance between neighboring defects can be maximized when the supercell basis vectors form square or hexagonal lattices. Grain boundary models generally require a very small lattice mismatch, as mentioned above. A good strategy to obtain such models is to design the supercells of the grains to have basis vectors spanning a lattice close to a square or hexagonal lattice because there is no degree of freedom on the aspect ratio in these two lattices. The supercell sizes of the two grains need to be chosen to have roughly the same area, hence finding an almost square or hexagonal lattice with a given supercell size is important.

2. Lattice analysis

Information on atom positions is irrelevant when handling basis vectors. The lattice can be handled with low computational cost using a hypothetical ‘empty’ cell where a virtual atom exists on every lattice point [31]. Use of primitive basis vectors (a_P, b_P) has the benefit that point ξa_P + ηb_P is a lattice point if, and only if, the 2D fractional coordinates ξ and η are both integers.

2D lattice parameters of a supercell are defined as $a=\left|\mathbf{a}\right|$, $b=\left|\mathbf{b}\right|$, and $\gamma ={cos}^{-1}\frac{\mathbf{a}\mathbf{.}\mathbf{b}}{ab}$. The area spanned by the basis vectors is denoted as

(1) $s=absin\gamma .$(1)

The aspect ratio is defined as

(2) $\kappa =b/a,$(2)

which is exactly 1 in square and hexagonal 2D supercells.

2.1. Reduced 2D primitive cell

The supplied inputs are an arbitrary 3D unit cell that may or may not be a supercell, the surface orientation (hkl), and the target 2D supercell size n with respect to the primitive cell. There is no limitation on the third direction of the 2D unit cell; the ‘2D unit cell’ can be a monolayer, slab separated by vacancies, or a portion of a 3D bulk. Generation of a primitive cell with basis vectors (a₀, b₀, c) where a₀ and b₀ are basis vectors spanning the (hkl) orientation, which is denoted as a (hkl)-primitive cell, and how to reduce the basis vectors is discussed in Hinuma et al. [31] ‘Reduced’ means that the basis vectors are the two non-zero shortest lattice vectors that are not linearly dependent. An alternate approach is given in Ref [32]. The Cartesian coordinates of lattice points do not change after the various manipulations in the algorithms presented in this work, thus a 3D unit cell can be recovered from a 2D unit cell by simply adding c as the third basis vector.

A reduced primitive 2D cell with basis vectors (a_P, b_P) is used as the starting point. The additional limitation of |a_P|≤|b_P| is imposed to make a_P the shorter basis vector, and the handedness of (a_P, b_P, c) is taken to be the same as (a₀, b₀, c). The area of the 2D cell with basis vectors a_P and b_P is

(3) $s=\left|{\mathbf{a}}_{\mathrm{P}}\times {\mathbf{b}}_{\mathrm{P}}\right|$(3)

The final basis vectors of the n-supercell are expressed as (a, b), and S in Equation (1)(1) $s=absin\gamma .$(1) is obtained by

(4) $S=ns=\left|\mathbf{a}\times \mathbf{b}\right|$(4)

2.2. List of lattice vectors shorter than a certain length

This section provides a procedure to find all 2D lattice vectors under a certain length λ. A 2H × 2K supercell centered at the origin can capture all lattice vectors shorter than λ when $H\ge \lambda \left|{\mathbf{b}}_{\mathrm{P}}\right|/s$ and $K\ge \lambda \left|{\mathbf{a}}_{\mathbf{P}}\right|/s$ (proposition 5 in Ref [33], the 3D version is given as lemma 4 in Ref [33]). The in-plane direction of a vector against a reference vector is best expressed in the range $0^{\circ }\le \phi <{360}^{\circ }$, which parallels the concept of ‘bearing’ in navigation (Figure 1) although the number increases in different directions (counterclockwise and clockwise, respectively). Using the notation $\theta \left(\mathit{u},v\right)={cos}^{-1}\frac{\mathit{u}\cdot \mathit{v}}{\left|\mathit{u}\right|\cdot \left|\mathit{v}\right|}$ where $0^{\circ }\le \theta <{180}^{\circ }$, the direction of a vector $\mathit{v}$ with respect to a is given by the following, which is based on supplementary material 3 in Ref [34]:

Figure 1. The definition of the direction φ with respect to a reference vector a. Vectors a and b are basis vectors, and the direction is defined such that the direction of b with respect to a is between 0 and 180°. The direction is obtained differently for regions I to IV, which are divided by black lines (see Equation 5).

$\phi =\theta \left(\mathbf{a},\mathit{v}\right)\mathrm{i}\mathrm{f}\theta \left(\mathbf{a},\mathit{v}\right)+\theta \left(\mathit{v},\mathbf{b}\right)-\theta \left(\mathbf{a}\mathbf{,}\mathbf{b}\right)=0^{\circ }$

$\phi =\theta \left(\mathbf{a},\mathit{v}\right)\mathrm{i}\mathrm{f}\theta \left(\mathbf{a},\mathit{v}\right)-\theta \left(\mathit{v},\mathbf{b}\right)-\theta \left(\mathbf{a}\mathbf{,}\mathbf{b}\right)=0^{\circ }$

$\phi ={360}^{\circ }-\theta \left(\mathbf{a},\mathit{v}\right)\mathrm{i}\mathrm{f}\theta \left(\mathbf{a},\mathit{v}\right)+\theta \left(\mathit{v},\mathbf{b}\right)+\theta \left(\mathbf{a}\mathbf{,}\mathbf{b}\right)={360}^{\circ }$

(5) $\phi ={360}^{\circ }-\theta \left(\mathbf{a},\mathit{v}\right)\mathrm{i}\mathrm{f}\theta \left(\mathbf{a},\mathit{v}\right)-\theta \left(\mathit{v},\mathbf{b}\right)+\theta \left(\mathbf{a}\mathbf{,}\mathbf{b}\right)=0^{\circ }$(5)

The four equations correspond to regions I to IV in Figure 1, respectively. These regions are the four quadrants when b is perpendicular to a, but b does not need to be perpendicular to a when deriving the direction of v.

Each lattice vector $\xi {\mathbf{a}}_{\mathrm{P}}+\eta {\mathbf{b}}_{\mathrm{P}}$ can be written in the form $h^{\prime }{\mathbf{a}}_{\mathrm{C}}+k^{\prime }{\mathbf{b}}_{\mathrm{C}}+l^{\prime }{\mathbf{c}}_{\mathrm{C}}$ where a_C, b_C, and c_C are basis vectors of the conventional cell and $h^{\prime }$, $k^{\prime }$, and $l^{\prime }$ are coefficients. A list of relevant lattice vectors and their ξ, η, $h^{\prime }$, $k^{\prime }$, $l^{\prime }$, φ with respect to a shortest lattice vector, $\xi {\mathbf{a}}_{\mathrm{P}}+\eta {\mathbf{b}}_{\mathrm{P}}$ in Cartesian coordinates, and length $L=\left|\xi {\mathbf{a}}_{\mathrm{P}}+\eta {\mathbf{b}}_{\mathrm{P}}\right|$ is used in the subsequent processes. Here, ξ and η are always integers, while $h^{\prime }$, $k^{\prime }$, and $l^{\prime }$ are always integers in a non-centered cell but may not be integers in a centered cell. The lattice vectors in the list are generally all lattice vectors should be shorter than a certain cutoff, and the list should be sorted by L and then by φ.

3. Supercell search procedure

The convention that 2D basis vectors a, b, and a vector pointing out of the page is right-handed is used.

3.1 Alikeness measures

Dimensionless measures are defined that quantifies the alikeness of the supercell to rectanglar, square, or hexagonal lattices. The measures are analogous to the objective function that is optimized in evolutionary algorithms. A measure of a rectangular supercell is

(6) $m_{\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}}=\left|\mathbf{a}\cdot \mathbf{b}\right|/S=\left|cot\gamma \right|$(6)

that takes the smallest possible value of 0 in a rectangular supercell.

A measure of a square supercell,

(7) $m_{\mathrm{s}\mathrm{q}}=\frac{a^2+b^2}{S}-2=\left(\kappa +\frac{1}{\kappa }\right)\frac{1}{sin\gamma }-2$(7)

takes the smallest possible value of 0 in a square supercell because κ = 1 and sin γ = 1.The basis vector b in Figure 2(a) can be minimized, while maintaining the same S and a, if b is chosen such that γ becomes as close to 90° as possible. The smallest value of $a^2+b^2$ is attained when a = b from the algebraic-harmonic mean relation.

Figure 2. Basis vector choices for almost (a) square and (b) hexagonal lattices.

A contour plot of m_sq(κ,γ) is given in Figure 3(a). The function m_sq(κ,γ) has the following characteristics (1): m_sq(κ) = m_sq(1/κ) (2), m_sq(κ,γ = fixed) is a convex function that is minimized when κ = 1, and (3) m_sq(κ = fixed,γ) is a convex function that is minimized when γ = 90°.

Figure 3. Contour plots for (a) m_sq and (b) m_hex as functions of κ and γ.

Choosing a measure of a hexagonal supercell is somewhat tricky. Figure 2(b) shows an almost hexagonal lattice. The convention of γ ≈ 120° is adopted. There are three distinct choices of a, which are a, a₂, and a₃. The corresponding basis vectors are b, b₂, and b₃. Three centered (almost) rectangular supercells with basis vectors (a, ${\mathbf{b}}^{\prime }=\mathbf{a}+2\mathbf{b}$), (a₂, ${{\mathbf{b}}^{\prime }}_2$), and (a₃, ${{\mathbf{b}}^{\prime }}_3$) are considered, which are shown in gray in Figure 2(b). These parallelograms have the same area of 2S, and the three parallelograms are exactly rectangular and congruent in an exact hexagonal lattice. A measure of a hexagonal supercell is proposed as

(8) $\begin{array}{c}{m}_{\mathrm{h}\mathrm{e}\mathrm{x}}=\left|\mathbf{a}\cdot {{\mathbf{b}}^{\prime }}_1\right|/S+\left|{\mathbf{a}}_2\cdot {{\mathbf{b}}^{\prime }}_2\right|/S+\left|{\mathbf{a}}_3\cdot {{\mathbf{b}}^{\prime }}_3\right|/S\\ =\left(\left|{\left|{\mathbf{a}}_2\right|}^2-{\left|{\mathbf{a}}_3\right|}^2\right|+\left|{\left|{\mathbf{a}}_3\right|}^2-{\left|\mathbf{a}\right|}^2\right|+\left|{\left|\mathbf{a}\right|}^2-{\left|{\mathbf{a}}_2\right|}^2\right|\right)/S\\ =\left(\left|1/\kappa +2cos\gamma \right|+\left|\kappa -1/\kappa \right|+\left|\kappa +2cos\gamma \right|\right)/sin\gamma \end{array}$(8)

A contour plot of m_hex(κ,γ) is shown in Figure 3(b). The function m_hex(κ,γ) has the following features (1): m_hex(κ) = m_hex(1/κ) (2), m_hex(κ,γ = fixed) is a mostly convex function that is minimized when κ = 1 (3), m_hex(κ = fixed,γ) is a convex function that is minimized when γ = 120°, and (4) $m_{\mathrm{h}\mathrm{e}\mathrm{x}}\left(\kappa ,{120}^{\circ }+\mathrm{\Delta }\gamma \right)>m_{\mathrm{h}\mathrm{e}\mathrm{x}}\left(\kappa ,{120}^{\circ }-\mathrm{\Delta }\gamma \right)$ when κ is fixed and Δγ>0.

All of the alikeness measures m are quantitative quantities that describe the ‘alikeness’ of a 2D supercell to a certain lattice (rectanglar, square, or hexagonal lattice). A value closer to zero is preferable, but m = 0 cannot be generally attained because of geometrical constraints. A ubiquitous ‘acceptable’ threshold value of m cannot be designated, especially as the smallest possible m for a given supercell size n tends to decrease with n (see Section 4.3). The values of m_rect, m_sq, and m_hex cannot be directly compared between each other.

3.2. Finding an almost rectangular n-supercell

The order of basis vector lengths a ≤ b can be assumed without loss of generality, and only one of a and -a need to be studied because the pairs of basis vectors (a,b), (−b,a), (−a,−b), and (b,−a) have the same m_rect. Therefore, lattice vectors with direction φ (see Section 2.2) in the range 0° ≤ φ < 180° with respect to a_P are chosen as candidates for a; the direction is determined such that the direction of b_P with respect to a_P is less than 180°. The direction of lattice vector candidates of b must be in the range 0° ≤ φ < 180° with respect to the considered a candidate.

An almost rectangular n-supercell is defined as a supercell where b is maximally orthogonalized to a, or in other words, has the shortest possible length among other choices. The upper bound of the length of a when a ≤ b is $a_{max}=\sqrt[4]{4/3}\sqrt{S}<1.075\sqrt{S}$ from lemma 1-(e) in Ref [33]. Figure 4 shows the relation between various vectors and important lengths. When $\mathbf{a}={\xi }_1{\mathbf{a}}_{\mathrm{P}}+{\eta }_1{\mathbf{b}}_{\mathrm{P}}$ and n is given, the counterpart basis vector has the form

Figure 4. Geometry for almost rectangular and square supercell derivation.

(9) $\mathbf{b}=\frac{n}{g}\mathit{r}+\frac{p}{g}\mathbf{a}$(9)

and points to the n/g-th row of lattice points parallel to a. Here, the greatest common divisor (GCD) of |ξ₁| and |η₁| is denoted as g, and n/g must be an integer to have a solution. The distance between the n/g-th row of lattice points and a is S/a (green dashed line in Figure 4). Vector r is an arbitrary lattice vector to a lattice point in the nearest row of lattice points parallel to a. The convention where a, r, and a vector pointing out of the page are right-handed is adopted, and one such vector can be derived using the algorithm in the Appendix. The handedness convention requires n > 0. The integer p is chosen such that the projection of b on a has length a/2g or less, or in equation form, $-a/2g\le \mathbf{b}\cdot \mathbf{a}/a\le a/2g$ (bounds shown as two blue dashed lines). The projection of $\frac{n}{g}\mathit{r}$ along a is $\frac{n\mathit{r}\cdot \mathbf{a}}{ga}$, hence p is an integer satisfying

(10) $-\frac{a}{2g}\le \frac{n\mathit{r}\cdot \mathbf{a}}{ga}+\frac{a}{g}p\le \frac{a}{2g}$(10)

For all a candidates, which are lattice vectors with length not exceeding a_max, the counterpart b that satisfies the above, which is one or two per a, is calculated. Pairs (−b,a), (−a,−b), and (b,−a) are additionally derived and reported for each (a,b) pair except when a = b where only (−a,−b) is additionally returned to avoid double counting. The pair of basis vectors can be each described using the set of coefficients $h^{\prime }$, $k^{\prime }$, and $l^{\prime }$ when denoted in the form $h^{\prime }{\mathbf{a}}_{\mathrm{C}}+k^{\prime }{\mathbf{b}}_{\mathrm{C}}+l^{\prime }{\mathbf{c}}_{\mathrm{C}}$. And additionally providing the lattice parameters a, b, and γ together with the corresponding measure, m_rect, is useful for further analysis.

Rectangular supercells with a large aspect ratio have applications in dislocation simulations, where the supercell is short along the dislocation line and long in other directions. An edge dislocation model could be obtained using computer assistance by using a thin layer of bulk as a ‘2D’ unit cell, making a 2D supercell taking the Burgers vector parallel to a and the dislocation line parallel to b, and the 3D supercell is derived by choosing the other basis vector c through taking an appropriate 1 × 1 × L supercell of the 2D supercell.

3.3 Finding an almost square n-supercell

The order of basis vector lengths a ≤ b can be assumed without loss of generality as in the almost rectangular supercell case. Again, the length of the projection of b on a, $\mathbf{b}\cdot \mathbf{a}/a$, must be within the range $-a/2g\le \mathbf{b}\cdot \mathbf{a}/a\le a/2g$, otherwise a shorter choice of b is available.

A strategy to limit the choice of a candidates while reducing computational cost is to obtain, for each a, the best and worst possible values of κ, κ_best and κ_worst, respectively (note that κ ≥1 because b with length b < a are not allowed), and also for γ, γ_best and γ_worst, and then obtain the lower and upper bounds of m_sq, which are m_sq- = m_sq(κ_best, γ_best) and m_sq+ = m_sq(κ_worst, γ_worst), respectively. The m_sq+ and m_sq- for all a candidates with $a_{max}=\sqrt[4]{4/3}\sqrt{S}<1.075\sqrt{S}$ are obtained. The search is relatively quick as the most computationally intensive operation is taking square roots. Candidates with m_sq- larger than a certain cutoff are removed from consideration; note that a smaller m_sq is preferable and there is a lower bound on m_sq, which is 0, but there is no upper bound on m_sq. The cutoff may be an arbitrary value or, if only the choice of basis vectors with the smallest m_sq is important, the smallest m_sq+ among all candidates. The vector b corresponding to each a is obtained as in the almost rectangular case (Section 3.2).

The bounds on b are

(11) $b_{-}=\frac{S}{a}\le b\le \sqrt{{\left(\frac{S}{a}\right)}^2+{\left(\frac{a}{2g}\right)}^2}=b_{+}$(11)

(see the geometry in Figure 4), and

${\kappa }_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}=1\mathrm{i}\mathrm{f}{b}_{-}\le a\le b_{+}$

(12) ${\kappa }_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}=b_{-}/a\mathrm{i}\mathrm{f}a<b_{-}<b_{+}$(12)

The situation $a>b_{+}$ never happens because a < b is assumed in the first place. For the worst case,

(13) ${\kappa }_{\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{t}}=b_{+}/a$(13)

The range of γ satisfies $\left|tan\left({90}^{\circ }-\gamma \right)\right|<\frac{a^2}{2S}$, and using trigonometry identities yields

(14) $1\le \frac{1}{sin\gamma }\le \sqrt{1+\frac{a^4}{4S^2}}$(14)

Therefore,

(15) $m_{\mathrm{s}\mathrm{q}-}=\left({\kappa }_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}+1/{\kappa }_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}\right)-2$(15)

and

(16) $m_{\mathrm{s}\mathrm{q}+}=\sqrt{1+\frac{a^4}{4S^2}}\cdot \left({\kappa }_{\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{t}}+1/{\kappa }_{\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{t}}\right)-2$(16)

There is one caveat in this formalism: when b is the counterpart basis vector that forms an almost square supercell for a particular basis vector choice a, then −a is not necessarily the counterpart basis vector for b. As more choices are better than less choices and m_sq can be used to quantitatively rank preferential basis vector choices, the proposed procedure does not require basis vector pairs (a,b) to satisfy “b is a counterpart of a” AND “−a is a counterpart of b”. However, “b is a counterpart of a” OR “−a is a counterpart of b” must be met. An example is given in Section 3.5.

3.4. Finding an almost hexagonal n-supercell

Only one of -a and -a need to be studied because the pair of basis vectors (a,b) and (−a,−b) have the same m_hex. In contrast to the almost rectangular and square cases, basis vectors (a,b) and (−b,a) do not share the same m_hex, thus both a ≤ b and b < a situations must be considered.

3.4.1 When a ≤ b

Figure 5(a) illustrates how to obtain b when a and S are given and a ≤ b. Here, b points to somewhere on the green dashed line, which is the line parallel to a separated by S/a, and between the outer blue dashed lines. The angle between a and the blue lines is 120°. The basis vector b is obtained using the procedure for the almost rectangular case (Section 3.2), but the range of integer p in Equation (9)(9) $\mathbf{b}=\frac{n}{g}\mathit{r}+\frac{p}{g}\mathbf{a}$(9) is changed from Equation (10)(10) $-\frac{a}{2g}\le \frac{n\mathit{r}\cdot \mathbf{a}}{ga}+\frac{a}{g}p\le \frac{a}{2g}$(10) to

Figure 5. Geometry for almost hexagonal supercell derivation.

(17) $-\frac{S}{\sqrt{3}a}-\frac{a}{2g}\le \frac{n\mathit{r}\cdot \mathbf{a}}{ga}+\frac{a}{g}p\le -\frac{S}{\sqrt{3}a}+\frac{a}{2g}$(17)

The restriction n > 0 still applies. The two boundaries are shown in purple lines in Figure 5(a). The bounds on b are, when the limitation a ≤ b is set aside for now,

(18) $b_{-}=min\left(\frac{S}{a},\sqrt{{\left(\frac{S}{\sqrt{3}a}-\frac{a}{2g}\right)}^2+{\left(\frac{S}{a}\right)}^2}\right)\le b\le \sqrt{{\left(\frac{S}{\sqrt{3}a}+\frac{a}{2g}\right)}^2+{\left(\frac{S}{a}\right)}^2}=b_{+}$(18)

The value of a must not exceed the largest possible value of b for the corresponding a. Therefore, the upper bound of a, a_max, must satisfy a_max < b₊(g = 1, a = a_max), and a_max can be given in the closed form of

(19) $a_{max}\le \frac{\sqrt{2}\sqrt{\sqrt{39}+\sqrt{3}}}{3}\sqrt{S}<1.332\sqrt{S}.$(19)

Going back to Equation (18)(18) $b_{-}=min\left(\frac{S}{a},\sqrt{{\left(\frac{S}{\sqrt{3}a}-\frac{a}{2g}\right)}^2+{\left(\frac{S}{a}\right)}^2}\right)\le b\le \sqrt{{\left(\frac{S}{\sqrt{3}a}+\frac{a}{2g}\right)}^2+{\left(\frac{S}{a}\right)}^2}=b_{+}$(18) and imposing a ≤ b,

${\kappa }_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}=1\mathrm{i}\mathrm{f}{b}_{-}\le a\le b_{+}$

(20) ${\kappa }_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}=b_{-}/a\mathrm{i}\mathrm{f}a<b_{-}<b_{+}$(20)

There is no κ when $a>b_{+}>b_{-}$ because a ≤ b. For the worst case,

(21) ${\kappa }_{\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{t}}=b_{+}/a$(21)

The range of γ satisfies

(22) ${\gamma }_{-}={cot}^{-1}\left(-\frac{a^2}{2S}+\frac{1}{\sqrt{3}}\right)\le \gamma \le {cot}^{-1}\left(-\frac{a^2}{2S}-\frac{1}{\sqrt{3}}\right)={\gamma }_{+}$(22)

Therefore,

(23) $m_{\mathrm{h}\mathrm{e}\mathrm{x}-}=m_{\mathrm{h}\mathrm{e}\mathrm{x}}\left({\kappa }_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}},{120}^{\circ }\right)$(23)

and

(24) $m_{\mathrm{h}\mathrm{e}\mathrm{x}+}=max\left(m_{\mathrm{h}\mathrm{e}\mathrm{x}}\left({\kappa }_{\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{t}},{\gamma }_{-}\right),m_{\mathrm{h}\mathrm{e}\mathrm{x}}\left({\kappa }_{\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{t}},{\gamma }_{+}\right)\right)$(24)

3.4.2 When b < a

Figure 5(b) shows the geometry when b < a. The vector a points to somewhere on the green dashed line, which is the line parallel to b separated by S/b, and between the outer blue dashed lines. The angle between b and the blue lines is 120°. In a style analogous to Equation (9)(9) $\mathbf{b}=\frac{n}{g}\mathit{r}+\frac{p}{g}\mathbf{a}$(9) ,

(25) $\mathbf{a}=-\frac{n}{f}\mathit{r}+q\mathbf{b}$(25)

where the GCD of |ξ₁| and |η₁| in $\mathbf{a}={\xi }_1{\mathbf{a}}_{\mathrm{P}}+{\eta }_1{\mathbf{b}}_{\mathrm{P}}$ is denoted as f, n/f must be an integer, and r is an arbitrary lattice vector to a lattice point in the nearest row of lattice points parallel to b. The handedness convention requires n < 0. The integer q is chosen such that the projection of a on b has length b/2f or less, or in equation form. $-b/2f\le \mathbf{b}\cdot \mathbf{a}/b\le b/2f$. Equation 17(17) $-\frac{S}{\sqrt{3}a}-\frac{a}{2g}\le \frac{n\mathit{r}\cdot \mathbf{a}}{ga}+\frac{a}{g}p\le -\frac{S}{\sqrt{3}a}+\frac{a}{2g}$(17) in Section 3.4.1 becomes

(26) $-\frac{S}{\sqrt{3}b}-\frac{b}{2f}\le -\frac{n\mathit{r}\cdot \mathbf{b}}{fb}+\frac{b}{f}q\le -\frac{S}{\sqrt{3}b}+\frac{b}{2f}$(26)

Here, a, g, and r in Equation (17)(17) $-\frac{S}{\sqrt{3}a}-\frac{a}{2g}\le \frac{n\mathit{r}\cdot \mathbf{a}}{ga}+\frac{a}{g}p\le -\frac{S}{\sqrt{3}a}+\frac{a}{2g}$(17) are substituted by b, f, and -r, respectively. The values of m_hex- and m_hex+ can be calculated as in Section 3.4.1 but with the above substitutions.

3.5. Finding an almost square n-supercell corresponding to a given basis vector

This procedure is worked out first in a trivial situation of a square lattice with lattice parameter of 1. The smallest square ‘supercell’ is the primitive cell with an exactly square shape and area 1. The basis vector length is 1. Using the second shortest lattice vector with length √2 as the basis vector results in a square 2-supercell. The square supercell using the third shortest lattice vector, with length 2, as a basis vector is a 4-supercell. There is no 3-supercell that is the supercell that is most alike to a square for any given basis vector. No solutions exist for some n, thus reporting solutions for all n below a given upper bound, n_max, is reasonable in this section and for the hexagonal analogue in Section 3.6.

A reduced cell can fit in a circle with a diameter of

(27) $2r=\sqrt{{a_{\mathrm{p}}}^2+{b_{\mathrm{p}}}^2+2a_{\mathrm{p}}{b}_{\mathrm{p}}\left|cos\gamma \right|}$(27)

which is the length of the longer diagonal of the reduced primitive cell (top right circle in Figure 6(a), the ratio of lattice parameters b to a is 3.357 and γ = 83.157°). In other words, there is always a lattice point within a circle with diameter 2r. Assuming a_P ≤ b_P.

Figure 6. Derivation of the counterpart basis vector b of the almost (a) square and (b) hexagonal supercell with basis vector a. The reduced unit cell and the circumscribed circle with diameter 2r is shown in the top right of (a). The vector t is the same length as a. There is no b for the right side drawings with short a. The ratio of lattice parameters b to a is 3.357 and γ = 83.157°.

(28) $2r\le \sqrt{{\left(\frac{3a_{\mathrm{p}}}{2}\right)}^2+{\left(\frac{s}{a_{\mathrm{p}}}\right)}^2}$(28)

because 2r is the length of the diagonal of a triangle where the length of one edge is at most (a_P + a_P/2) and the other is s/a_P.

Figure 6(a) illustrates how to obtain basis vector b when a is given. A vector t is drawn with length a and direction φ = 90°. The endpoint of basis vector b forming an almost square n-supercell with a should lie in a circle of radius r centered at the endpoint of t. The annulus sector that encompasses the circle has inner radius a-r, outer radius a+r.

The allowed values of γ satisfy ${90}^{\circ }-{sin}^{-1}r/a\le \gamma \le {90}^{\circ }+{sin}^{-1}r/a$, which is well-defined when r ≤ a and the origin of t is not inside the circle (left side of Figure 6(a), the origin is on the circle in the edge case of r = a). The lattice vectors in this annulus sector can be easily identified, by using comparison operators only, from the list of L and φ discussed in Section 2.2. In case of r > a, where ${sin}^{-1}r/a$ is ill-defined (right side of Figure 6(a)), lattice vectors with $0^{\circ }\le \gamma \le {180}^{\circ }$ and lengths between 0 and a + r are shortlisted. Basis vector candidates that are not in the radius r circle are then eliminated from consideration. The m_sq is subsequently obtained for all candidates of b to find the candidate(s) that minimizes m_sq. The determined b is shown in the left side of Figure 6(a). There is no candidate of b in the green circle in the right side, and the algorithm determines that there is no almost square supercell for the provided a in such cases.

The basis vector b = −a_P + 2b_P is a counterpart for all of a = 5a_P, 6a_P, 7a_P, and 8a_P. The four (a,b) pairs are all considered ‘almost square n-supercells corresponding to a given basis vector’ with n = 10, 12, 14, and 16, respectively. The counterpart of a = −a_P + 2b_P is b = −7a_P. Forcing basis vector pairs (a,b) to satisfy “b is a counterpart of a” AND” −a is a counterpart of b” rejects the pairs (5a_P, −a_P + 2b_P), (6a_P, −a_P + 2b_P), and (8a_P, −a_P +2b_P). However, this maneuver removes choices for n = 10 and 12 supercells, which would be inconvenient when n = 10 or 12 supercells are desired.

In contrast to Sections 3.2 to 3.4, the longer basis vector needs to be included in the exhaustive list of lattice vectors under a certain cutoff length obtained using Section 2.2. An upper bound on a for an almost square n-supercell is derived below. The area of a supercell with basis vector a, S_a, is in the range $a\left(a-r\right)\le S_a\le a\left(a+r\right)$. Note that the basis vector b always points to a lattice point in the green circle and not anywhere in the annulus sector in Figure 6(a). If $a_{max}\left(a_{max}-r\right)=S_a=ns$, this a_max is the longest possible a for an almost square n-supercell and thus a satisfies

(29) $a\le \frac{\sqrt{r^2+4ns}}{2}+r$(29)

The maximum length of lattice vectors that need to be searched using Section 2.2 is $\frac{\sqrt{r^2+4ns}}{2}+2r$

3.6. Finding an almost hexagonal n-supercell corresponding to a given basis vector

The procedure is almost the same as in the square supercell case. The quantity r is defined as $2r=\sqrt{{a_{\mathrm{p}}}^2+{b_{\mathrm{p}}}^2+2a_{\mathrm{p}}{b}_{\mathrm{p}}\left|cos\gamma \right|}$ (same as Equations (27(27) $2r=\sqrt{{a_{\mathrm{p}}}^2+{b_{\mathrm{p}}}^2+2a_{\mathrm{p}}{b}_{\mathrm{p}}\left|cos\gamma \right|}$(27) , 28(28) $2r\le \sqrt{{\left(\frac{3a_{\mathrm{p}}}{2}\right)}^2+{\left(\frac{s}{a_{\mathrm{p}}}\right)}^2}$(28) also holds). If r ≤ a, lattice vectors in the annulus sector of inner radius a - r, outer radius a + r, and γ satisfying ${120}^{\circ }-{sin}^{-1}r/a\le \gamma \le min\left({120}^{\circ }+{sin}^{-1}r/a,{180}^{\circ }\right)$ are searched (left side of Figure 6(b)) and if r > a, lattice vectors with length between 0 and a + r as well as $0^{\circ }\le \gamma \le {180}^{\circ }$ are identified (right side of Figure 6(b)). Basis vector candidates that are not in the radius r circle are eliminated from consideration, and the candidate with smallest m_hex is chosen as the basis vector b. There may be no basis vector candidate when r > a, which is the case in the right side of Figure 6(b).

The same b can appear in almost hexagonal n-supercells corresponding to a given basis vector a, as in the almost square case. As an example, the counterpart of both a = 6a_P and 7a_P is b = −4a_P + 2b_P, resulting in n = 12 and 14 supercells. For the record, there is a smaller m_hex combination for n = 12, which is (a,b) = (2b_P, −6a_P−b_P), while (7a_P, −4a_P−2b_P) is the smallest m_hex choice for n = 14.

An upper bound on a for an almost hexagonal n-supercell is deduced as follows. The area of a supercell with basis vector a, S_a, is in the range $a\left(\sqrt{3}a/2-r\right)\le S_a\le a\left(\sqrt{3}a/2+r\right)$. If $a_{max}\left(\sqrt{3}{a}_{max}\text{break}/2-r\right)=S_a=ns$, this a_max is the longest possible a for an almost hexagonal n-supercell and satisfies

(30) $a\le \frac{\sqrt{r^2+2\sqrt{3}ns}+r}{\sqrt{3}}$(30)

The maximum length of lattice vectors that need to be searched using Section 2.2 is $\frac{\sqrt{r^2+2\sqrt{3}ns}+r}{\sqrt{3}}+r$.

4. Supercell search procedure

4.1 Rectangular supercell of baddeleyite structure ZrO₂ (11$\bar{\mathbf{1}}$)

The most stable surface of baddeleyite structure ZrO₂ (space group P2₁/c) is (11$\bar{1}$) [35]. The 2D primitive basis vectors are described using 3D conventional basis vectors as a_P = a_C + c_C and b_P = a_C −b_C, and the calculated 2D lattice parameters are a = 6.820 Å, b = 7.388 Å, and γ = 63.516°. Figure 7(a) illustrates the (11$\bar{1}$) surface. The lattice is close to a hexagonal lattice. There are three obvious choices of an almost rectangular 2-supercell, (a₁, b₁), (a₂, b₂), (a₃, b₃). and the basis vectors are given in white, pink, and blue, respectively. The values of m_rect and lattice parameters of the supercell a, b, and γ are (0.0174, 6.820 Å, 13.228 Å, 90.998°), (0.1070, 7.388 Å, 12.278 Å, 83.895°), and (0.0895, 7.494 Å, 12.085 Å, 95.117°), respectively. Therefore, the first supercell is regarded as closest to rectangular.

Figure 7. (a) (11$\bar{1}$) surface of baddeleyite structure ZrO₂. Three basis vector choices for a 2-supercell are indicated, which are (a₁, b₁), (a₂, b₂), and (a₃, b₃) (shown in white, blue, and pink arrows, respectively). Green and red circles indicate Zr and O, respectively, while the outermost O are shown in orange. (b) (101) surface of anatase structure TiO₂. This 2D lattice is centered rectangular. The basis vectors of the primitive cell are (a_P, b_P), and an exactly rectangular 2-supercell is shown with basis vectors (a_P, b_r) (black arrows). An almost square 3-supercell and an almost hexagonal 5-supercell are is shown with basis vectors (a_s, b_s) and (a_h, b_h), respectively (pink and green arrows, respectively). Blue and red circles indicate Ti and O, respectively, while the outermost O are shown in orange.

4.2 Almost square and hexagonal supercells of anatase structure TiO₂ (101)

The most stable surface of anatase structure TiO₂ (space group I4₁/amd) is (10$\bar{1}$) [35]. The 2D primitive basis vectors are described using 3D conventional basis vectors as a_P = a_C + c_C and b_P = a_C −b_C. The calculated 2D reduced lattice parameters are a = 3.857 Å, b = 5.502 Å, and γ = 69.479°, while the 2D conventional lattice parameters are a = 3.857 Å, b = 10.306 Å, and γ = 90°, The primitive cell area is 19.878 Ų. Figure 8(a) illustrates the (101) surface. The lattice is centered rectangular. The conventional cell has basis vectors (a_P, b_r). There is an almost square 3-supercell, with basis vectors (a_s, b_s) and m_sq = 0.0135, at./=b=7.748 Å, and γ = 96.628°. Besides from the almost square 4- and 6-supercells that are very obvious (2 × 1 and 3 × 1 supercells of the conventional cell, m_sq = 0.0844 and 0.0135, respectively), there is an almost hexagonal 5-supercell with basis vectors (a_s, b_s) and m_hax = 0.2685, a = b = 10.934 Å, and γ = 123.767°.

Figure 8. (a) m_sq and (b) m_hex versus n for almost square and hexagonal supercells of a sc lattice, respectively. ‘Magic numbers’ n are labeled.

4.3 Almost square and hexagonal supercells of a sc lattice

The almost square and hexagonal supercells of the {100}, {110}, and {111} orientations of a sc lattice obtained through Sections 3.5 and 3.6 are discussed. The results described here are not necessarily limited to sc lattices only because 2D lattices of these orientations are also found in other crystals. The {100} orientation is a square lattice also found in the {100} orientation of the bcc and fcc lattices as well as the {001} orientation of simple and body-centered tetragonal lattices. The {110} orientation is a rectangular lattice with b/a ratio of √2, and the {111} orientation is a hexagonal lattice found in the {111} orientation of bcc and fcc lattices and the {0001} orientation of 3D rhombohedral and hexagonal crystals.

The almost square supercells of the {100} orientation is trivial; all of them are m_sq = 0 and allowed n satisfy n= h² + k² where h and k are integers. There are eight symmetrically equivalent supercells when all of h≠0, k≠0, and |h|≠|k| holds, and four otherwise.

Figure 8(a) plots m_sq and n of almost square supercells for the {110} and {111} orientations, as obtained using Section 3.5. The value of m_sq tends to decrease as n increases. There are a number of ‘magic number’ n, which are indicated with arrows in Figure 8(a), where the m_sq is considerably smaller than those of nearby n. These n and one choice of a and b are, for the (110) orientation: (n = 6, a = −2a_C + 2b_C, b = −3c_C), (n = 35, a = 7c_C, b = −5a_C + 5b_C), and (n = 204, a = −12a_C + 12b_C, b = −17c_C), and for the (111) orientation: (n = 15, a = 4a_C −3b_C −c_C, b = a_C + 3b_C −4c_C), (n = 56, a = 8a_C −4b_C −4c_C, b = 7b_C-7c_C), and (n = 209, a = 15a_C −11b_C −4c_C, b = 4a_C + 11b_C −15c_C). The basis vectors of the sc (111) orientation can be converted to those of a hexagonal (001) orientation using a_h = a_c −b_c and b_h = b_c −c_c. Using these hexagonal basis vectors, the magic numbers for the (001) orientation become (n = 15, a = 4a_h + b_h, b = a_h + 4b_h), (n = 56, a = 8a_h + 4b_h, b = 7b_h), and (n = 209, a = 15a_h +4b_h, b = 4a_h +15b_h).

The almost hexagonal supercells of the {111} orientation are all m_hex = 0 and allowed integer n satisfy n=(h-k/2)² +3k²/4 where h and k are integers. The list of such n is: 1, 3, 4, 7, 9, 12, 13, 16, 19, 21, 25, 27, 28, 31, 36, 37, 39, 43, 48, 49 … This sequence appears in the calculated ground state structures in the Na battery cathode and thermoelectric compound P2-Na_xCoO₂; there are ground states at x = 10/13, 13/16, 16/19, and 18/21, where x=(n-3)/n [36]. There are eight symmetrically supercells when all of h≠0, k≠0, and |h|≠|k| holds and four otherwise.

Figure 8(b) plots m_sq and n of almost hexagonal supercells for the {100} and {110} orientations found using Section 3.6. The value of m_sq tends to decrease as n increases as in the almost square supercells in Figure 8(a). Again, there are a number of ‘magic number’ n, which are indicated with arrows in Figure 8(b), where the m_hex is considerably smaller than those of nearby n. These n and one choice of a and b are, for the (100) orientation: (n = 15, a = 4b_C + c_C, b = −3b_C + 3c_C), (n = 56, a = 8b_C, b = −4b_C + 7c_C), and (n = 209, a = 15b_C + 4c_C, b = −11b_C + 11c_C), and for the (110) orientation: (n = 20, a = −4a_C + 4b_C, b = 2a_C − 2b_C −5c_C), (n = 109, a = −2a_C + 2b_C + 13c_C, b = −7a_C + 7b_C −9c_C), and (n = 198, a = −11a_C + 11b_C + 9c_C, b = −18c_C).

5. Conclusions

This study proposed quantitative measures on how much a 2D supercell is close to a rectangular, square, or hexagonal lattice. Procedures to make supercells, of arbitrary crystals, with a given size and alikeness to these lattices were given. The outlined algorithms would be useful in defect calculations, including desorption and absorption, because convenient supercell shapes can be used. Almost epitaxial interface models can be generated by finding an almost square or hexagonal 2D supercell for each side, with a carefully chosen supercell size to reduce the small lattice mismatch, that serves as an approximate 2D CSL.

Acknowledgements

The VESTA code [38] was used to draw Figures 2 and 4–7.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This study was funded by Kakenhi Grant-in-Aid for Transformative Research Areas(B)[No. 21H05101] from the Japan Society for the Promotion of Science (JSPS).

Appendix

Finding a lattice vector to the neighboring row of lattice points

This section discusses finding a lattice vector $\mathit{r}={\xi }_2{\mathbf{a}}_{\mathrm{P}}+{\eta }_2{\mathbf{b}}_{\mathrm{P}}$ that points to a lattice point in a closest row of lattice points parallel to a lattice vector $\mathbf{a}={\xi }_{\mathrm{a}}{\mathbf{a}}_{\mathrm{P}}+{\eta }_{\mathrm{a}}{\mathbf{b}}_{\mathrm{P}}$, where a_p and b_P are basis vectors of a primitive cell. The GCD of |ξ_a| and |η_a| is denoted as g, amd the vector ${\mathbf{a}}^{\prime }=\left(1/g\right)\mathbf{a}={\xi }_1{\mathbf{a}}_{\mathrm{P}}+{\eta }_1{\mathbf{b}}_{\mathrm{P}}$ is defined. There are two closest rows and here the row such that a, r, and a vector pointing out of the page is right-handed is chosen.

The vector ${\mathbf{b}}^{\prime }=-{\eta }_1{\mathbf{a}}_{\mathrm{P}}+{\xi }_1{\mathbf{b}}_{\mathrm{P}}$ is never linearly dependent to a, and there are exactly m = ξ₁²+η₁² lattice points with the form $\mathit{v}={\xi }^{\prime }\mathbf{a}+{\eta }^{\prime }{\mathbf{b}}^{\prime }$ where $0\le {\xi }^{\prime }<1$ and $0\le {\eta }^{\prime }<1$. Note that v can represent a lattice vector even when ${\xi }^{\prime }$ and ${\eta }^{\prime }$ are not integers because a and ${\mathbf{b}}^{\prime }$ are not necessarily basis vectors of a primitive cell). The vector r can also be expressed as $\mathit{r}={\xi }_2^{\prime }{\mathbf{a}}^{\prime }+{\eta }_2^{\prime }{\mathbf{b}}^{\prime }$ where

(31) $\left(\begin{array}{cc}{\xi }_2& {\eta }_2\end{array}\right)=\left(\begin{array}{cc}{{\xi }^{\prime }}_2& {{\eta }^{\prime }}_2\end{array}\right)\left(\begin{array}{cc}{\xi }_1& {\eta }_1\\ -{\eta }_1& {\xi }_1\end{array}\right)$(31)

or

(32) $\left(\begin{array}{cc}{{\xi }^{\prime }}_2& {{\eta }^{\prime }}_2\end{array}\right)=\frac{1}{{{\xi }_1}^2+{{\eta }_1}^2}\left(\begin{array}{cc}{\xi }_2& {\eta }_2\end{array}\right)\left(\begin{array}{cc}{\xi }_1& -{\eta }_1\\ {\eta }_1& {\xi }_1\end{array}\right)$(32)

when ${\eta }_2^{\prime }$ should be the smallest positive value. Therefore, $-{\eta }_1{\xi }_2+{\xi }_1{\eta }_2=1$.

One solution of (ξ₂, η₂) can be obtained using the Euclidean algorithm solving method by Blankinship [37]. The first element of a row is referred to as the leader of the row.

1. A 2 × 3 matrix is defined as $\left(\begin{array}{cc}\begin{array}{c}-{\eta }_1\\ {\xi }_1\end{array}& \begin{array}{cc}1& 0\\ 0& 1\end{array}\end{array}\right)$.

2. If $-{\eta }_1<0$, change row 1 to $\left(\begin{array}{ccc}{\eta }_1& -1& 0\end{array}\right)$.

3. If ${\xi }_1<0$, change row 2 to $\left(\begin{array}{ccc}-{\xi }_1& 0& 1\end{array}\right)$.

4. Loop the following while the leader of row 2 is not zero.

   • (4a) Divide the leader of row 2 into the leader of row 1, ignoring the remainder. Denote the quotient by Q.

   • (4b) Subtract Q times row 2 from row 1.

   • (4c) Switch rows 1 and 2.

5. The first row is $\left(\begin{array}{ccc}1& {\xi }_2& {\eta }_2\end{array}\right)$.