Alloys innovation through machine learning: a statistical literature review

ABSTRACT

This review systematically analyzes over 200 publications to explore the growing role of data-driven methods and their potential benefits in accelerating alloy development. The review presents a comprehensive overview of different aspects of alloy innovation by machine learning and other computational approaches used in recent years. These methods harness the power of advanced simulation techniques and data analytics to expedite materials’ discovery, predict properties, and optimize performance. Through analysis, significant trends and disparities within the data discerned, while highlighting previously overlooked research gaps, thus underscoring areas that require further exploration. Machine Learning techniques are widely applied across various alloys, with a pronounced emphasis on steel and High Entropy Alloys. Notably, researchers primarily investigate the physical, mechanical, and catalytic properties of materials. In terms of methodology, while 68% of the examined papers rely on a single machine learning model, the remainder employ a range of 2 to 12 models, with Neural Network being the most prevalent choice. However, a notable concern arises as 53% of these papers do not share their dataset, and a staggering 81% do not provide access to their code. Paramount importance of adopting a systematic approach when scrutinizing machine learning methodologies is underscored. Analysis shows lack of consistency and diversity in the methods employed by researchers in the field of alloy development, highlighting the potential for improvement through standardization. The critical analysis of the literature not only reveals prevailing trends and patterns but also shines a light on the inherent limitations within the traditional trial-and-error paradigm.

GRAPHICAL ABSTRACT

IMPACT STATEMENT

Through statistical analysis of 200+ papers, this research identifies trends, patterns and gaps to highlight areas for further exploration in using machine learning for alloy development.

KEYWORDS:

• Alloy development
• machine learning
• data-driven research
• materials informatics
• materials genome initiative
• materials databases

1. Introduction

Owing to high-speed computers, networks, and massive storage cloud spaces, nowadays artificial intelligence (AI), and machine learning (ML) have proven that they could considerably speed up fundamental and applied materials science research [1,2]. This paper explores the profound impact of AI and ML algorithms and techniques, which have used in an era of unprecedented materials discovery and development across a wide spectrum of material types, including structural materials, catalysts, high-entropy alloys (HEA), superalloys, shape-memory alloys, magnetic materials, and energy storage materials that their study can be complicated and complex.

For instance, when it comes to the mechanical properties of an alloy, achieving the desired properties necessitates providing a balance between accurate prediction and occasional envisioning. An example of such studies is reported by Olson et al. [3]. Using a classic materials search approach, they looked to design a new alloy that has less nickel and copper to reduce its cost while preserving the look of the alloy, its excellent corrosion properties, and its electrical conductivity [3]. The pursuit of optimal trade-offs within these complex and complicated systems is facilitated by ML. While an increasing number of scholars have harnessed ML techniques to ascertain the optimal trade-off, several key inquiries persist, including the identification of the most suitable ML technologies and models, which remain unaddressed.

This paper represents a comprehensive synthesis of insights drawn from a meticulous statistical analysis of over 200 publications. Specifically, the study focuses on peer-reviewed journals that employ rigorous methodologies, featuring a diverse array of ML models. Each publication presents its optimal model, contributing to the broader understanding of the field. All the papers under study are succinctly summarized within the main text and are visually represented in the accompanying graphs. Consequently, these papers are duly cited in the reference section of this research.

Chapter 2 offers a global perspective on the field’s evolution and tracing its development over the years. Chapter 3 provides a comprehensive overview of the alloys under examination. Chapter 4 delves into the application of ML in alloy development by covering predicted parameters, dataset sizes, ML optimization, and commonly used models. Mechanical property prediction, model accuracy, and alignment with first principles and CALPHAD are explored. We also address data generation challenges and presented the best suggested ML models. Chapter 5 reviews various ML deployment strategies, while Chapter 6 focuses on data and code availability in publications. Lastly, Chapter 7 concludes our journey by summarizing findings and providing an outlook for the field’s future.

The present review offers a specific perspective on ML-driven research within the domain of alloy development. It elucidates critical methodologies, applications, theoretical predictions, and experimental validations. Furthermore, it presents the results of various studies, comparing and discussing discrepancies and contradictions while identifying gaps in the existing literature. The primary objectives of this research endeavor are as follows:

1. To gain a comprehensive understanding of the prevailing ML models and technologies employed by researchers to address multifaceted challenges in materials science research.

2. To uncover underlying patterns and correlations among diverse material features.

3. To analyze the structures and dynamics of ML approaches, as well as the intricate interconnections between models, structures, and properties.

4. To discern the impacts and implications of various compositional elements, considering experimental procedures, with potential implications for decision-making and policy.

5. To determine the optimal scenarios for utilizing experimental research data versus computational data.

6. To identify the ML models recommended by researchers for predicting desired alloy properties.

Throughout this study, data visualization techniques, such as bar charts, pie charts, and Sankey graphs, are employed to enhance the clarity of the narrative. These visual aids provide a holistic perspective on the landscape of ML research within the materials science domain. It is worth noting that this review exclusively encompasses publications in the English language, with publications in other languages excluded from consideration.

In summary, this paper addresses a critical juncture in materials science research, where the convergence of AI and ML is poised to reshape the landscape of materials discovery, development, and innovation. The insights presented herein have profound implications for researchers, policymakers, and practitioners seeking to harness the power of AI and ML in the pursuit of advanced materials with tailored properties and applications.

2. Current ML development in the world

Diverse national contingents of researchers have manifested distinct methodological inclinations in their research to harness ML for alloy development. This study has undertaken a comprehensive analysis, systematically extracting the first author’s country of origin from each publication, thereby elucidating the myriad national strategies and approaches employed in the application of ML for advancing alloy development. Figure 1 shows a bar chart detailing publications analyzed in this review from 1995 to 2022, including the first authors’ countries. The graph shows that before 2012, a few papers used ML for alloy development while the number increased by time. It is worths to mention that ML studies regained scientific interest in late 2014 and the beginning of 2015 when the Google speech recognition program was already launched [4]. Publications within the domain exhibited a substantial upswing, notably in the years 2016 and 2017, with the U.S.A. at the forefront of this surge. Nevertheless, commencing from 2020, China surpassed the U.S.A. in terms of the volume of papers published in this field. It is worth mentioning that in this research, the affiliated country of the first author of every publication is considered the country of that publication.

Figure 1. Chart shows the quantity of research publications studied in this paper, organized by the year of publication and the first author’s country.

Figure 2 shows the distribution of publications across different journals in the field of using ML in alloy development. Notably, a significant number of journals cover this topic, with 67% of the papers distributed among various journals, demonstrating a wide dissemination of research. It is evident that publication in this field is not confined to a limited number of journals. Computational Materials Science, in particular, has a notable 10% share of publications, highlighting its significant contribution to the literature in this domain.

Figure 2. Pie chart displaying the proportion of publications in different peer-review journals that were studied in this research.

3. Alloys

The allocation of scholarly interest among countries exhibits intriguing patterns, emphasizing the diverse approaches of distinct national research bodies. Figure 3 shows a Sankey diagram illustrating the various alloys and materials studied by ML by every country. Most of cited researchers in this work have studied steel, HEA, and Aluminum (Al) alloys. The vast majority of research contribution are held by China and U.S.A., followed by the UK, India and the rest of the world. Steels, HEA and Al-based alloys consist of large number of publications due to their obvious industrial importance. Range of alloys, Catalysts, Ti-based alloys, and Metallic glasses are also of great interest for most of these countries. The term ‘Range of Alloys’ indicates the publications that looked at a range of alloys instead of focusing on one alloy with a single base metal. It is noticeable that China’s publications are focused more on steel, HEA, metallic glass, and magnesium alloys, while the U.S.A. focuses on steel, catalysts, and HEA.

Figure 3. Sankey diagram with countries on the left side and studied alloys by ML on the right side.

In their publications, researchers from the U.S.A. have frequently explored a wide range of alloys, a practice less commonly observed among researchers from other nations. This highlights a notable difference in the approach to alloy consideration, with U.S.A.-based researchers demonstrating a penchant for encompassing multiple alloys within a single publication, a tendency not as commonly shared by their counterparts from other countries. The sankey diagram offers a comprehensive visual representation of how different countries engage in ML research pertaining to various alloys and highlights distinctive research among these nations. Further elaboration on the research about each specific alloy is presented in this chapter.

This chapter examines the alloys studied in this research and demonstrates the required properties of these alloys, as well as presenting the approaches researchers have employed to address these challenges.

3.1. Aluminum alloys

Aluminum-based alloys are widely used in many applications, such as the aerospace and automotive industry, because of their low density, high strength, and low production-maintenance costs. Compared to steel, aluminum-based alloys have a strength disadvantage. Al-alloys are heat-treated to attain high strength, with experimental procedures often needing to be optimized or difficult to control [5]. Modeling is valuable for reducing experimental procedures; however, it bears its own inherent limitations. So, researchers have employed ML techniques to address this challenge.

For instance, the modeling of crystal nucleation in aluminum or amorphization, requires the construction of interatomic interactions that can reproduce the properties of both the solid and the liquid states. The simulation necessary to capture such a mechanism may take much larger capacity beyond the capability of first-principles calculations. Marchand et al. [6] have presented the first family of NN potentials to describe the binary Al-Cu system with comparable accuracy to the first-principles method. The newly developed potentials could be used to predict elastic constants, solid solution of dilute systems, interfaces, stacking faults, intermetallic compounds, and defect energies. This demonstrated the clear advantage of using the ML approach. Also, Jakse et al. [7] have studied the solidification process in aluminum by simulations on the atomic scale by coupling classical molecular dynamics simulations and a NN. A set of configurations relevant to solidification phenomena were generated.

Özhavak et al. [8] have used a Convolutional NN algorithm, ANN, and Random Forest (RF) regression to determine the change in mechanical properties of AA2024 aluminum produced with different manufacturing methods after aging at various temperatures and times. The Convolutional NN obtained the best accuracy of 93%.

Kumar et al. [9] studied the performance of decision tree, RF, and XGBoost ML models to determine the best classifier model for a friction stir welded AA 6061-T6 aluminum alloy. The XGBoost model showed a maximum accuracy of about 96% among the three models, which shows promising results that help lower the time and cost of manufacturing these alloys. Yao et al. [10] have proposed a parameter identification method based on semi-coupled damage mechanics and ML to describe the fracture behavior of 6061 aluminum alloy. A set of reliable parameters were generated to circumvent extracting the stress state evolution from the calibrated specimens. Due to the large demand for its wide applications, modern parts based on 6XXX series aluminum are recently produced by additive manufacturing techniques, where developing ML predictions is essential for 3D printing parameter optimization. Based on Gaussian process regression, Liu et al. [11] have developed a ML approach to identify the optimized processing window for laser powder bed fusion. The newly predicted processing parameters helped to print dense new AlSi10Mg alloys with a higher ultimate tensile strength between 297 and 389 MPa, and an elongation to failure from 6% to 10%. Yanase et al. [12] have examined the densification behavior and microstructural formation of the Al–10 mass %Si–0.35 mass %Mg alloy fabricated using the Selective Laser Melting method based on experimental work and NN ML approach. The combined techniques have identified the required processing factor which quantitatively influences the behavior. Using a back-propagation NN algorithm, Chun et al. [13] could accurately predict manufacturing parameters for aluminum alloys, such as flow stress, roll force, and roll torque.

Li et al. [14] studied the relationship between alloy composition, process parameters, and mechanical properties, using a genetic algorithm combined with backpropagation and radial basis function NN to develop the properties of 7XXX aluminum alloys. The accuracy of combining the NN with the genetic algorithm was superior to that of those predicted by the NN and radial function. Predicted fine and dispersed spherical precipitates formed after aging heat treatment were observed experimentally by SEM and HRTEM, confirming that their mixed approach may greatly assist metallurgists in developing 7XXX aluminum alloys. Aydin [15] has studied the volume loss of AA7075 with 5 wt% Al₂O₃ composites under load, using linear regression, support vector regression (SVR), ANN, and extreme learning machine for the prediction. The extreme learning machine approach showed the highest R² coefficient compared to other methods, which shows the model’s remarkable ability to predict the wear behavior of aluminum composites. Decke et al. [16] have focused on predicting the hot deformation behavior of thermo-mechanically processed precipitation-hardenable aluminum alloy AA7075 based on a comparative study of modeling techniques based on ML and the Zerilli – Armstrong modeling. They could predict stress–strain curves using the gradient boosting model as their best model with an accuracy of 91%.

Haghdadi et al. [17] have estimated the high-temperature flow behavior of a cast A356 aluminum alloy using a feed-forward back propagation NN with a single hidden layer composed of 20 neurons for a series of isothermal compression tests. The results demonstrate that the NN model is a robust tool for predicting the high-temperature flow behavior of cast A356 aluminum alloy.

Shang et al. [18] reported the characterization of the dynamic hardening behavior of an aluminum alloy, sheet of 5182-O (wrought alloy), for strain rate and temperature coupling effect. Polynomial algorithm and ANN were used to describe the highly non-linearity and coupling of strain hardening. The study found that the network structure, parameter setting, and optimization algorithm have affected the ANN prediction accuracy. Using ML, Soofi et al. [19] have estimated the properties of commercial wrought aluminum alloys. Starting from a small dataset of 236 features, six mechanical and nine technological properties, they could capture composition/processing-property relations.

Takara et al. [20] used multiple regression with supervised learning to predict the linear relationship between voids and their corresponding elemental compound composition.

Lian et al. [21] have predicted the fatigue life of aluminum alloy using a ML framework combined with empirical formulas and data-driven models. They used gradient boost regression to predict the fatigue life of seven different series of aluminum alloys, achieving a great improvement compared to conventional models. Their findings successfully demonstrated the advantages of the ML approach, which provides a unique way to predict fatigue life to reduce the time and cost of experiments. Similarly, Chun et al. [22] have proposed an RF ML method to predict structural damage from vibrational measurements in aluminum alloys.

Several reports about the ML prediction of equilibrium phases, composition, and thermal transport were published. Jiang et al. [23] have developed a new ML model to predict the quasi-phase equilibrium equations for multicomponent alloys to reduce the long time required to solve such equations. A NN model of three inputs, four outputs, and a hidden layer of 150 nodes was tested to study the quasi-phase equilibrium during the isothermal solidification of Al-Cu-Mg alloy. Dai et al. [24] classified five types of aluminum alloys using laser-induced breakdown spectroscopy combined with principal component analysis and least-squares support vector machine (SVM) algorithm. An accuracy of 100% was achieved, suggesting the model is an efficient approach to identifying aluminum alloys. In a similar way, Wang et al. [25] have studied thermal transport in aluminum with precipitate morphology. They developed a Finite Element Method to create a database. A correlation analysis was conducted from the obtained data to evaluate the importance of various precipitate features. Thermal conductivity was predicted by linear regression, Bayesian Ridge, Kernel Ridge, Nearest Neighbors, and RF. In similar way, ML can uncover hidden patterns and correlations that elude traditional approaches. Thus, the heightened understanding enables the precise manipulation of alloy characteristics to achieve desired outcomes.

3.2. Titanium alloys

Researchers published a range of publications on adopted ML and data-driven strategies to further develop titanium alloys. Malinov and Sha [26,27] have proposed an ML model based on ANNs for modeling correlations between processing parameters and properties in titanium alloys and γ-TiAl-based alloys. Combined with computer programs for optimization of the inputs, the ANN models could be powerful tools for practical applications in solving various problems in titanium alloys.

Zhu et al. [28] have proposed a titanium alloy design method based on experiments and ML. The work discusses the effect of Mo and Cr on the microstructure and mechanical properties of newly developed titanium alloys (Ti–3Al–2Nb-1.2 V–1Zr–1Sn-xCr-yMo). The predicted results agree with experimental values. The mechanical test result shows an excellent balance of strength (Yield Strength ~1200 MPa) and plasticity (Elongation ~ 12%) can be achieved after the solution treatment at 750°C and ageing at 550°C for 6 h. Using heat assisted single-point incremental forming, Bautista-Monsalve et al. [29] have reported ML-based procedure for the determination of the surface finish quality of titanium alloy parts.

Currently, additive manufacturing technology is widely used in fabricating titanium alloy parts for aerospace applications. Zhan et al. [30] have reported a Data-driven fatigue life prediction in additive manufactured titanium alloy. The paper presents a damage mechanics-based ML framework for additive manufacturing titanium alloy’s data-driven fatigue life prediction. The work presents a theoretical framework for the damage mechanics-based fatigue models and a strategy to compute the damage and the construction process. An RF model was used, and the predicted results were compared with the experimental data to verify the proposed method. Li et al. [31] have presented ML-based very-high-cycle fatigue life prediction of Ti-6Al-4 V alloy fabricated by selective laser melting. Sun et al. [32] have reported developing a constitutive relationship model of Ti600 alloy using an ANN.

To capture the effect of alloying elements and the influence of the heat-treatment on the stability of titanium alloys, an ML approach based on an ANN modeling was proposed by Reddy et al. [33].

Kwak et al. [34] have predicted the mechanical properties of γ-TiAl alloys produced using an RF regression model. The accuracy of the prediction results was evaluated using the R² value. The R² values were 0.9336, 0.9902, 0.8104, and 0.9810, for the tensile strength, elongation, nanoindentation hardness, and interlamellar space, respectively.

Ti-6Al-4 V titanium is a difficult-to-cut material used in critical applications in the aerospace industry requiring high-reliability levels. Selecting the cutting conditions can improve the machinability of the alloy, including the generation of compressive residual stresses. The work by Outeiro et al. [35] proposed orthogonal cutting tests of Ti-6Al-4 V titanium were performed, and a designed experiment was used to investigate the influence of the cutting conditions on residual stresses, the forces, and the chip compression ratio. The residual stress was only measured for selected cutting conditions due to the time consumed and the high cost. An ML regression model was applied to predict the residual stresses for other cutting conditions. Wu et al. [36] have proposed an ensemble NNs model that is developed for targeting the effects of alloying elements on phase stability and low Young’s modulus of Ti alloys. The work also provided guidelines for future material designs considering the stability of β phase and discussed the effects of some alloying elements, such as Nb, Zr, Mo, Sn, and Ta.

3.3. Magnesium alloys

Improving the strength of magnesium alloys is still a challenge that is limiting its potential applications as a lightweight metal. ML can help in the development of high-strength Mg alloys. Liu et al. [37] have used a surrogate model to optimize the composition and heat treatment conditions of Mg cast alloys. A new alloy with the composition of Mg-10.0Al-2.0Sn-2.0Zn-0.1Ca-0.1Mn (at. %) was identified, aged at 200°C for 96 h. The alloy shows a Vickers hardness value superior to the conventional alloy.

Because of many variances from different suppliers, the mechanical properties of AZ31 magnesium alloys are hard to control. Xu et al. [38] proposed a ML approach using the ANN and the SVM algorithms to understand better the relationship between alloy compositions, processing parameters, and mechanical properties. The yield strength, ultimate tensile strength, and tensile elongation were predicted by both models, and a new AZ31 extruded alloy was fabricated.

Ibarra-Hernández et al. [39] have used a combination of a NN algorithm with metaheuristic structural global search algorithms to screen the Mg – Ca binary system for new (meta)stable alloys. This allows for efficient exploration of the potential energy surface beyond the possibility of the traditional searches based on ab initio calculations. Some low-enthalpy structures were identified at different stoichiometries.

Gui et al. [40] have used a novel Mg-4Y-3Nd-2Sm-0.5Zr alloy prepared to explore the twin nucleation behavior of Mg alloys by combining ML and electron backscattered diffraction techniques. Three ML algorithms, including gradient boosting, ANN, and the proposed relevance-based ensemble scheme, are used to model to predict the twin nucleation. The AUC score was 0.880, 0.879, and 0.756 for the proposed relevance-based ensemble scheme, ANN, and gradient boosting, respectively.

Wei et al. [41] have collected 150 pieces of the work function of Mg-based solid solutions and Mg-containing second phases to build an initial dataset estimated by density functional theory. Fourteen features were used as input variables. Four ML models, including multiple linear regression, support vector regression (SVR), gradient boosting regression tree, and extreme gradient boosting tree, were used to predict the work function of the second phase. The result shows that the SVR model has the highest accuracy and best generalization ability.

Fang et al. [42] have used a linear regression model to investigate the relationship between the widths of supercooled liquid regions of Mg-based bulk metallic glasses and bond parameters. They deduced an equation for the first time to predict whether Mg-based multicomponent alloys can form metallic glasses.

To analyze the solution behavior of a second element in the primary phase of α-Mg, Chen et al. [43] have collected the interaction features of solutes and Mg obtained from first-principles calculation, the intrinsic physical properties of the pure elements and structural features. They have used RF and decision tree algorithm methods and found that the solution behavior of an element in α-Mg can be affected mainly by four features: formation energy, electronegativity, non-bonded atomic radius, and work function.

3.4. Copper, cobalt, and additive manufactured alloys

Qiao et al. [44], Wang et al. [45], Rovinelli et al. [46], Wang et al. [47], Zhang et al. [48], Seko et al. [49] used various ML methods, such as ANNs, GAs, Bayesian networks, RFs, etc. to predict and optimize the properties of copper alloys with different alloying elements, such as Co, Ni, Si, Cr, Zr, etc. These studies used different features to represent the alloys, such as elemental composition, thermodynamic data, microstructural parameters, etc., and different ML models to capture the non-linear relationships between the features and the properties.

Another application of ML methods for copper alloys is to design alloys with specific colors for art and decoration purposes. For example, Reitz and Barojas [50], Oh et al. [51], Chintakindi et al. [52], Yang et al. [53] used various ML methods, such as Monte Carlo simulation, feature-assisted ML algorithms, principal component analysis (PCA), hyper-parameter optimization, etc., to predict and optimize the color values of copper alloys with different alloying elements, such as Al, Zn, Sn, etc. These studies used different features to represent the alloys, such as elemental composition, annealing temperature, color coordinates, etc., and different ML models to capture the complex color phenomena.

A third application of ML methods for copper alloys is to model the mechanical behavior and microstructural evolution during deformation and heat treatment processes. For example, Mayeur et al. [54], van Nieuwenburg et al. [55], Sun et al. [56], Fu et al. [57], Kautz et al. [58], Grabowski et al. [59] used various ML methods, such as crystal plasticity model with dislocation transport (CPDT), confusion matrix method (CMM), DNN, sensitivity analysis and ML surrogate model (SMLSM), image-driven ML approach (IDMLA), ab initio vibrational free energies including anharmonicity (AFEA), etc., to predict and optimize the mechanical properties and microstructural features of copper alloys with different alloying elements, such as Ni, Co, Si, Mo, etc.

3.5. High-entropy alloys

HEA are the vast majority of alloys treated by ML before aluminum alloys and steels. This top place is gained because of the complex nature of the alloys and a considerable number of possible configurations that could never be all calculated or fabricated.

Chang et al. [60] have utilized an ANN to predict the composition of HEAs applied to a non-equimolar AlCoCrFeMnNi to achieve high hardness. The work successfully predicted new compositions of AlCoCrFeMnNi-based HEAs, exhibiting hardness values higher than those available in the literature.

George et al. [61] have reported the implementation of gradient boosting trees ML algorithm trained on nearly 7000 ordered inorganic HEAs, with a combined experimental and computational approach based on in-situ neutron-diffraction characterizations and ab initio calculations, to explore and predict the elastic moduli of single-phase face-centered-cubic Al0.3CoCrFeNi HEAs. ML models trained on a large dataset could accurately predict the elastic properties of the alloys. The ML models demonstrated the dependence of bulk and shear moduli on several material features, which can help tune elastic properties in HEAs.

Qingfenget al. [62] have studied the eutectic formation of the Al-Co-Cr-Fe-Ni system as an example representative of HEA via an ANN algorithm. Essential elements and strongly associated elements were identified. Cr is strongly associated with Al, Ni, Co, and Fe. These findings can accelerate the employment of the algorithm in designing more complex alloys.

Menou et al. [63] have integrated a computational HEA design. Their strategy combines a multi-objective genetic algorithm with statistical criteria to guide the formation of a single phase, supplemented by computational thermodynamics (Thermo-Calc) to study solid solution-strengthening models. Many of non-equimolar face-centered-cubic single-phase alloys are designed. Best designed alloys are synthesized experimentally.

Also, the Menou et al. [64] used a multi-objective optimization genetic algorithm combining solid solution hardening and thermodynamic modeling (CALPHAD) with data mining to design HEA. The approach found the best stable alloys and designed several optimal HEA. Al35Cr35Mn8Mo5Ti17 (at.%) is chosen for experimental validation.

Zhuang et al. [65] have developed a method integrating a multicomponent diffusion-multiple and ML to study the effects of alloying elements, such as Ni, Al, W, Ti, Ta, Cr, Mo, and Nb, on the microstructures.

A class of ML potential called Moment Tensor Potential (MTP) has been developed and used by Jafary-Zadeh et al. [66] to predict the structure and elastic properties of the multi-principal element alloy.

Rickman et al. [67] have proposed an ML approach using supervised data fed to two complementary algorithms: multiple regression analysis and a genetic algorithm. The methodology is validated after identifying promising multi-principal elements with high hardness.

A study by Ozerdem and Kolukisa [68] has employed an ANN approach to predict the mechanical properties of Cu-Sn-Pb-Zn-Ni cast alloys. The ANN used multi-layer perceptron architecture with a back-propagation algorithm. The compositions were used as input, and yield strength, tensile strength, and elongation were employed as outputs to be predicted.

Zhang et al. [69] used molecular dynamics simulation combined with ML methods to study the mechanical properties of non-equiatomic Fe-Cr-Ni-Co-Mn HEAs. Molecular Dynamic simulation provided a database describing the relationship between material composition and mechanical properties. These properties are trained and investigated using three ML models, including SVM, kernel-based extreme learning machine, and DNN, for predicting the yield stress. The DNN model outperformed other models for the classification of yield stress.

Kostiuchenko et al. [70] have proposed a computational method for studying HEAs based on applying ML potentials derived from ab initio data in combination with Monte Carlo simulations. The approach is employed to study phase stability, phase transitions, and short-range chemical order.

Rao et al. [71] have integrated ML with density-functional theory, thermodynamic calculations, and experiments to predict high-entropy Invar alloys. The method led to the characterization of 17 new alloys, where two were identified as high-entropy Invar alloys with low thermal expansion.

Machaka et al. [72] have constructed a dataset based on 430 peer-reviewed experimental publications, including 40 metallurgy-specific predictor features. This study comprised eight ML classifiers: regression tree, linear discriminant analysis, naїve Bayes, generalized linear regression, RF, ANN, k-nearest neighbors, and SVMs. These classifiers were trained and evaluated to classify HEA solid solution phases across feature ensemble sizes.

Zhang et al. [73] proposed a systematic methodology based on a genetic algorithm to select the ML model and materials descriptors from many alternative HEAs. Several HEAs were selected and experimentally synthesized.

Batchelor et al. [74] have presented a theoretical method to find new active alloy electrocatalysts. Using the multicomponent Ir-Pd-Pt-Rh-Ru alloy, the alloy composition with the best predicted catalytic activity was found.

Using the concepts of Louvain and modified particle swarm optimization (PSO) algorithms, Nia et al. [75] tried to find correlations between HEA descriptors to predict HEA candidates with similar functionality. The proposed method predicted the HEA phase composition with an accuracy of 93%.

The gradient-boosting regression model was used by Wan et al. [76] to map the oxygen reduction reaction catalytic activity of millions of reactive sites on HEA surfaces. The model showed high accuracy and generalization, accurately predicting the catalytic activities of numerous reactive sites on HEA surfaces.

Clausen et al. [77] developed a methodology to predict the oxygen reduction reaction’s net catalytic activity in Ag-Ir-Pd-Pt-Ru alloy. Based on ab initio calculations, a graph convolution NN is used to predict adsorption energies of *OH and *O.

Mishra et al. [78] used ML models on design parameters using classification for HEA phase prediction. The ML models are RF, Stacked Ensemble, and SVM. The training dataset comprising 601 cast alloys is used with cross-validation for test data. The stacked ensemble was the best model, overperforming the SVM and RF.

Wen et al. [79] described a relationship derived from the electronegative difference of elements to characterize solid solution strengthening in the four HEAs: Al-Co-Cr-Fe-Ni, Co-Cr-Fe-Ni-Mn, Hf-Nb-Ta-Ti-Zr, and Mo-Nb-Ta-W-V. Their findings are based on ML methods involving feature construction and selection, which are essential to determining the most important descriptors.

Aided by ML-based interatomic potentials, Zhou et al. [80] developed an approach based on density-functional theory and computational thermodynamic integration to perform extensive screening in vast compositional space on an equiatomic HEA, Ta-V-Cr-W, and discovered the most stable ones, after comparing their free energies.

Numerous other studies covering many applications in HEAs, have included predictions of new alloys [81], phase formations [82,83], heterogeneous Grain Structures [84], large and enhanced hardness [85,86], strengthening mechanisms [87], formation energies [88], sublattice formation in Co-Cr-Fe-Ni [89], phase formations through considering the formation enthalpy and atom-size difference [90], configurational energy [91], quality prediction of additively manufactured alloys [45], stability and structure prediction of cubic phases [92], efficient exploration of the composition-phase space [93], the discovery of single-phase refractory [94], multi-objective optimization [95], selective CO₂ reduction to methanol [96] and discovery of high-entropy ceramics [97].

Different methods to design HEA were employed, such as thermodynamics and Gaussian process statistical analysis [98], mined from binary phase diagrams [99], statistical approaches [100] and feature engineering to characterize limited material datasets.

3.6. Steel

Similar to the developments and advances in aluminum and HEAs, a breakthrough in multi-component steel design also requires a comprehensive understanding of complex multi-phases. This necessitates the systematic exploration and screening of numerous prospective configurations across extensive composition ranges, where ML methodologies have the potential to provide valuable assistance.

Deng et al. [101], Wang et al. [47], Shin et al. [102], Geng et al. [103], Peng et al. [104], and Yang et al. [105] used ML methods to develop steel alloys and optimize their properties. These studies performed similar activities, such as predicting steel alloys’ elastic properties, creep life, and atmospheric corrosion resistance. However, they differ in the specific alloys and properties studied and the ML methods used.

Rakhshkhorshid and Sendesi [106], Zhan and Li [107], Thanush, et al. [108], Wang et al. [109], and Wang et al. [110] also used ML methods to develop steel alloys and predict their properties. These studies focused on predicting austenite formation temperatures, fatigue life, atmospheric corrosion rate, creep life, and molten salt corrosion resistance of steel alloys.

ML methods have been used to predict various properties of steel alloys such as austenite formation temperatures, rolling force in cold rolling, and optimal design of alloy steels [26,111–115]. ML also used to predict deformation behavior, high-temperature deformation behavior, ductile damage in sheet metal forming, stacking faulting energy in austenitic steels, materials defects [116–126], porosity in metal-based additive manufacturing, flow stress in hot deformation, tensile strength of alloy steels and high cycle fatigue performance of polycrystalline microstructures [127–134].

Fu et al. [57] and Rahnama et al. [135] used ML methods to predict various properties of steel alloys, such as grain structure after thermomechanical processing, kinetic modeling of a discontinuous precipitation reaction, vibrational free energies including anharmonicity for multicomponent alloys and the occurrence of interphase precipitation in High Strength Low Alloy (HSLA) steels.

One of the main applications of ML methods for maraging steels is to predict the tensile strength and hardness based on the composition and aging temperature. For example, Guo and Sha [131] used an ANN to model the correlation between processing parameters and properties of maraging steels. They found that the aging temperature significantly influenced tensile strength and hardness. Rao and Prasad [132] used a NN approach to evaluate the flow stress of maraging steels during hot deformation. They found that the flow stress increased with increasing strain rate and decreasing temperature. Gocheva-llieva and Dobrev [133,134] used polynomial regression to study the tensile strength of alloy steels and found that the tensile strength increased with increasing carbon and manganese content.

Another application of ML methods for maraging steels is to predict fatigue life and crack growth based on the microstructural features and loading conditions. For example, Paulson et al. [134] used data-driven reduced-order models to rank-order polycrystalline microstructures’ high cycle fatigue performance. They found that the grain size, grain orientation spread, texture coefficient, etc., influenced the fatigue life. Fu et al. [57] used sensitivity analysis and a ML surrogate model to predict the grain structure of U-10Mo alloy after thermomechanical processing. They found that the grain size distribution was affected by the rolling temperature, reduction ratio, annealing temperature and etc.

A third application of ML methods for maraging steels is to predict the precipitation kinetics and phase transformation behavior based on the thermodynamic data and kinetic models. For example, Kautz et al. [136] used an image-driven ML approach to model the kinetic behavior of a discontinuous precipitation reaction in a Fe-Ni-Cr alloy. They found that the precipitation rate was controlled by diffusion and interface migration. Grabowski et al. [59] used ab initio vibrational free energies, including anharmonicity, for multicomponent alloys and found that the vibrational entropy significantly affected the phase stability of Fe-Ni-Cr alloys. Rahnama et al. [135] used ML to predict the occurrence of interphase precipitation in HSLA steels. They found that the composition, cooling rate, austenite grain size, etc, influenced the interphase precipitation.

Deng et al. [101] have designed oxide dispersion-strengthened steel with a composition of Fe-12%Cr-4.5%Al-2.0%W-0.3%Y₂O₃ (wt%) by a radial basis function ANN and prepared by hot isostatic pressing. They found a small amount of Y-Al-O composite oxide, and its average size is significantly larger than Y₂O₃. The tensile strength and elongation measured at room temperature and 700°C are consistent with the predicted values of ML.

Wang et al. [47] have reported a ML approach using randomized trees and deep NNs to cluster expansion-generated data to predict the bulk and shear moduli of Fe-Cr-Al alloys. They found that the compositions and temperature are critical features in bulk modulus, while compositions, temperature, and the ordering effect are essential in shear modulus.

By combining measured creep data of a high-temperature alloy and alloy features derived from a computational thermodynamic approach, Shin et al. [102] have proposed a methodology to predict new creep-resistant alloys. The method has highlighted important features essential to better understanding new alloy designs.

A feedforward ANN model has been developed by Geng et al. [103] using relevant material descriptors, including chemical composition, to predict the hardenability of boron steel. The model has successfully predicted new steel with a good hardenability of 0.04% V-added boron steel.

3.7. Amorphous, shape memory, metallic glass, and catalytic materials

In the past, scientists and researchers have relied on domain knowledge, trial and error, and luck to obtain materials with optimized composition and process. Ling et al. [137] have proposed a methodology, called RFs with Uncertainty Estimates for Learning Sequentially (FUELS), built on an RF model, that can accelerate getting desirable materials by fitting data-driven models to experimental data.

Li et al. [138] have successfully generated and optimized ML models to predict the elastic properties of amorphous alloys by implementing six different algorithms, including linear algorithms (Lasso and Ridge) and nonlinear algorithms (RF, Extreme Gradient Boosting, SVR, ANN). The predictions agreed with glass forming ability and plasticity prediction ternary amorphous alloy systems.

Bulk-metallic glasses are a unique class of alloy materials utilized in various applications due to their attractive physical properties. Xiong et al. [139] have tested over 20 ML models to predict the properties of metallic glasses and amorphous metallic alloys. RF gave the best prediction for their study. The model predictions for a newly introduced dataset were in agree with the experimental results.

Tang et al. [140] have used ML to accelerate the design of Fe – based amorphous alloys with six magnetic desired properties. Linear Regression, Support Vector Regression, Decision Tree Regression, ANN, and RF Regression are employed to build prediction models. The ANN algorithm showed the best predictability with an accuracy of over 90% while the prediction yield into the design of Fe83-B9-P3-C4-Nb1, which was verified experimentally.

Artrith and Kolpak [141] have proposed an approach that combines site-based Monte-Carlo simulations to sample the composition space and molecular dynamics simulations for electrocatalysts suitable for sustainable energy applications. To describe the atomic interactions, they used ANN potentials to interpolate density-functional theory calculations. The equilibrium compositions at finite temperatures: 300 K and 500 K, are compared to the ground state configurations for Cu–Au nanoalloys.

Mueller [142] presented a theoretical study of Au-Pd nanoparticles. Using a Bayesian approach to cluster expansions, he has calculated the equilibrium atomic structures, energies, and the electronic surface d-band centers across the entire range of compositions at different temperatures. The prediction error of the estimated formation energies was lower than the error relative to density functional theory (1 meV/atom).

Cao et al. [143] have developed a method based on cluster expansions and density functional theory that may facilitate the rational design of new catalysts. The method is allowing scientists to quickly predict the near-surface atomic arrangement and catalytic properties, giving them the possibility to identify the synthesizing conditions of the best alloys.

Tran and Ulissi [144] have presented an automated computational screening approach, combining ML and optimization to guide density functional theory to predict electrocatalyst performance. They demonstrated the feasibility of this method by screening various alloys with different elements.

Gao et al. [145] have built a model based on an overlap of ML and atomic positions to accelerate the estimation of formation energies of amorphous alloys and considerably reduce the cost of the required DFT calculations. The results with high accuracy could help to develop the Pd40-Ni10-Cu30-P20 catalyst.

Yang et al. [53] have simulated a NN model based on DFT calculations to predict the potential energies across the Cu–Pd–Au ternary space. With reasonable accuracy, the simulation results qualitatively agree with the experimental data for PdAu and CuAu. Other important studies reporting advanced ML models used in predicting properties of Ni-P based amorphous alloys [146], and shape memory alloys [147–152].

Cai et al. [153] have reported the progress of component design methods for bulk metallic glass. The group reported extensive studies on the development of glass forming alloys by ANN, to reduce transition temperatures [154], modeling for undercooled liquid region [155], and predicting of critical cooling rate [156].

Among other methodologies of using ML in predicting forming metallic glasses, a two-step fused ML approach was used by Zhang et al. [157]. They used multivariate analysis and classification using principal component analysis. Tripathi et al. [158], a support vector classification method for predicting the glass-forming ability of binary metallic alloys from compositions, randomly selected. Sun et al. [159] were employed the same method to predict elastic properties and glass-forming ability of bulk metallic glasses. Xiong et al. [160] predicted the ability to exist in an amorphous state, critical casting diameter and supercooled liquid range by using decision trees and RF. Ward et al. [161] and Ren et al. [162] developed accelerated discovery of metallic glasses using ML iteration and high-throughput experiments.

In case of catalytic materials, ML used for a range of applications including the development of platinum-modified amorphous alloy surface catalysts [163], optimizing ternary catalytic alloy electrode for efficiency improvement of semiconductor performance [164], electrocatalytic for oxygen reduction [165], composition and activity of electrocatalytic nanoalloys in aqueous solvents [166], catalytic activity of nanoparticles [167], generated feature engineering of ML chemisorption modeling [168], bimetallic catalysts [169], scaling relations for the description of catalytic material and beyond [170], predicting binding energies by building convolutional NN for atomic surface structures [171], CO₂ electrocatalysts [172], and nanocatalysts for oxygen reduction reaction [173].

Other studies have covered vast scientific research areas naming: Inconel 718 alloys [174], thermoelectrics [175], CO₂ electroreduction catalyst screening [176], electronic density states [177], nanoclusters [178,179], casting parts [180], electrochemical curve simulation of corrosion and its application [181] and copper alloys [182]. The search for stable Cu-Pd-Ag nanoparticles [183] predicting stress hotspots in face centered cubic materials [184] search for rare-earth-free permanent magnets [185] were other research in the field. Predicted the Curie temperature of ferromagnets Nelson and Sanvito [186], the discovery of new half-heusler [187], low-thermal-conductivity of half-heusler semiconductors [188,189], elastic moduli of k-nary inorganic polycrystalline compounds [190], properties of metastable polymorph structures [191] amorphous LixSi [192] low-melting alloys [193] predicting properties of inorganic materials [194] and processing-structure relationships in soft magnetic alloys [195] were the next groups of research in the field.

3.8. Ni-based superalloy

Distinct groups could be identified upon careful examination of the abstracts of the selected papers on ML methods for developing nickel alloys. The first group comprises Tancret [196], Menou, et al. [197], and Conduit et al. [198], who shared a common focus on the design and optimization of nickel alloys. These papers employed various computational tools, optimization algorithms, and techniques such as computational thermodynamics, genetic algorithms, and data mining to optimize alloy compositions and achieve desired mechanical and microstructural properties.

The second group includes Jiang et al. [199], Chandran et al. [200], and Schooling et al. [201], who rather focused on the application of ML for a target property prediction. These papers explore lattice misfit prediction, estimation of interface energy, and modeling of fatigue thresholds in nickel alloys. They leverage ML algorithms, such as SVR, NNs, and neuro-fuzzy networks, to accurately predict and analyze several material properties. Taylor and Conduit [202] have used Gaussian process regression ML to predict good properties for laboratory and commercial Ni-based superalloys. Wu et al. [203] proposed a novel methodology for classifying multi-principal element alloys with excellent strength – ductility. They predicted a yield strength of more than 1 GPa and a ductility of over 20%. Islam et al. [204] have employed a NN in the ML framework to gain insights into designing multi-principal element alloys (MPEA) to recognize the underlying data pattern using an experimental dataset to classify the corresponding phase selection in MPEAs.

4. ML and alloy

This chapter presents the approaches of researchers using ML algorithms to address the challenges in alloy research. Their strategies for selecting predictive parameters, dataset size, and ML model optimization are examined. The most commonly employed ML models, including ensemble techniques and ANN, are also investigated. Furthermore, the chapter explores methodologies for designing and predicting mechanical properties and assesses the accuracy of ML models. Additionally, it delves into the utilization of first-principles, CALPHAD, and thermodynamics in related research. The challenges of data generation, high-throughput approaches, and image processing are discussed in detail. Finally, the most effective ML models are presented.

4.1. Predicted parameter

4.1.1. Predicted parameter, country and alloy

Choosing the right predicted parameter is crucial because ML is utilized to optimize specific alloy properties, a consistent focus in reviewed papers. The Sankey diagram of Figure 4 is structured with distinct columns for countries, predicted parameters, and the studied alloys. Notably, China emerges as a preeminent contributor, accounting for the highest volume of publications, dedicating 40% to the prediction of physical properties, 45% to mechanical properties and 15% on other parameters. In contrast, research publications from the U.S.A. allocate 35% toward physical properties, 26% toward mechanical properties, and 39% toward various other parameters. Significantly, a substantial proportion of research pertaining to catalytic properties (46%), crystal properties (77%), and process parameters (75%) originates from U.S.A. researchers. In the case of the United Kingdom, 50% of their research endeavors are centered on the prediction of physical properties, while 33% are focused on mechanical properties.

Figure 4. The Sankey diagram with the countries on the left side, predicted parameters in the middle and studied alloys on the right side.

In addition to the conventional single-parameter prediction approach, an alternative strategy has surfaced, wherein a combined and integrated approach is employed to simultaneously predict both physical and mechanical properties. This innovative methodology is exemplified in the references [12,37,44].

This collective analysis suggests that while researchers from diverse countries engage in predicting a spectrum of alloy properties, the U.S.A. exhibits a proclivity for a more extensive range of parameter prediction when employing ML techniques compared to their international counterparts. This implies a certain level of diversification and specialization in the global research landscape, with implications for the unique research priorities and strengths of each contributing nation.

Figure 4 reveals a comprehensive analysis of predicted parameters, encompassing a range of properties including mechanical and physical properties across a diverse array of alloys. Notably, the research landscape displays distinct tendencies, with 57% of studies focusing on steel, 58% on aluminum alloys, and 57% on titanium alloys to predict the mechanical properties. In contrast, the prediction of physical properties is notably prevalent in specific domains, with 25% of steel research, 65% of HEA investigations, 17% of aluminum alloys’ research, and 67% of metallic glass studies concentrating on this aspect. A salient observation pertains to the strong inclination among studies that encompass multiple alloys, where 60% of such research endeavors prioritize the prediction of physical properties, exemplifying the multifaceted nature of the research paradigm.

4.1.2. Predicted parameter and ML model

Various ML models are employed for predicting specific alloy properties and researchers are divided in choosing ML models to predict alloy properties. The Sankey diagram in Figure 5, shows the associations between predicted parameters and the corresponding ML models employed for prediction. 38% of researchers utilize NN for predicting mechanical properties, and 22% for predicting physical properties. An observed preference is noted for Linear Regression, where 60% of researchers employing this model for mechanical property prediction. Moreover, 40% of researchers resort to NN for predicting catalytic properties. Interestingly, 66% of researchers harness Gaussian Process to predict physical properties.

Figure 5. The Sankey diagram represents the associations between predicted properties (on the left side) and the corresponding ML models employed in the analysis, as evident from the collected publications (on the right side). The figure provides insights into the distribution and utilization of ML models for predicting specific properties in the context of the collected publications.

Further analysis reveals that predominantly, NN, RF, and SVM constitute the preferred ML models that collectively representing 20% of all models employed. Notably, NN is frequently utilized, with 40% of its applications dedicated to predicting both mechanical and physical properties. In the case of RF, 40% of its applications focus on predicting physical properties, while 40% are oriented toward mechanical properties. SVM allocations reveal 38% for mechanical property prediction and 34% for physical property prediction.

The co-utilization of ML models for predicting both mechanical and physical properties is evident that is highlighting the adaptability and utility of these models in alloy research. Researchers exhibit diverse preferences for ML models, and while certain models are specialized, others, like Linear Regression, have specific applications in the eyes of researchers.

4.2. Large/Small datasets, and raw data collection

The size of the dataset has a significant impact on the accuracy of ML models. A larger dataset can improve model accuracy by reducing overfitting and increasing generalization. However, most of dataset provided from metallurgy for ML applications are small and limited to few samples. Overfitting occurs when a model is trained too well on a small dataset and performs poorly on new data. A larger dataset can also enhance the robustness of a model by making it more resistant to noise and outliers. However, collecting large datasets of alloys can be expensive and time-consuming. One of most robust methods in materials search adapted for small dataset is based on a trade-off between an exploitation (ML model) and exploration (uncertainties) approaches. In this regard, Xue et al. [205] have developed an adaptive design strategy, coupled with experiments, that can accelerate the discovery process of NiTi-based shape memory alloys.

Several initiatives have emerged to build materials databases due to the Materials Genome Initiative, data-management policies enforced by funding agencies, and the recent awareness within the materials community of the positive impact of data sharing and dissemination. A wide range of databases, both empirical and computational, have become available that cover a diverse set of materials properties such as structures, formation energetics, thermodynamic phase diagrams, and electrical and mechanical properties across different material classes, including metals, ceramics, alloys, glasses, 2D materials and nanocomposites [62]. Table 1 shows some notable data repositories and their application in the studied publications. Although a few of these data repositories are frequently used by researchers, a significant number of them remain largely unnoticed. It is intriguing to note that researchers often struggle to create more data to make their ML models better, even though there is a lot of unused data in existing databases. We’ll delve deeper into this in Chapter 7, which titled ‘Data and Code Availability’.

Table 1. Known data repositories of metals and used in the collected papers.

Data repository	Refs
Open Quantum Materials Database (OQMD)	[6,163,174,175,190,207]
NIST ICSD	[39,113,198,200,207]
Materials Project database	[43,59,205,214]
NIST MATERIALS DATA REPOSITORY	[43,196]
MatNavi materials database by the National Institute for Materials Science, Japan	[108]
NOMAD	[178]
Pauling File	Not used
Cambridge Structural Database (CSD),	Not used
MatWeb	Not used
Total Metals	Not used
INTERGLAD	Not used
FIZ Karlsruhe ICSD	Not used
SpringerMaterials Databases	Not used
AFLOWLIB consortium	Not used
Material Go (MG)	Not used
CMR (COMPUTATIONAL MATERIALS REPOSITORY)	Not used

Researchers are facing a significant challenge arises in forming the libraries used for ML predictions. The most likely scenario is to consider multiple databases specialized around a specific type of desired data, e.g. first-principles calculations, crystallography, mechanical properties, Scanning Transmission Electron Microscopy (STEM) imaging, etc. Having open, well-documented, and standardized dataset models is essential in all cases to enable better integration [206].

Despite presenting intriguing research findings, some attempts in this review did not yield successful outcomes. One such endeavor was to compare the sizes of datasets used in constructing ML models. However, making such comparisons among published papers often proved challenging, as several studies did not provide information about the size of their datasets. In cases where data sizes were reported, there was considerable variability. For example, Tang et al. [140] utilized a dataset comprising 2083 inputs representing 36 different elements, while Yan et al. [94] mentioned 1807 entries. This is while some studies indicated just the number of rows and columns of the datasets [207,208]. These disparities made it difficult to establish clear dataset size comparisons. As a result, the dataset sizes often remained unreported. It would be beneficial for future research to standardize and report dataset sizes consistently for better comparisons.

4.3. ML optimization: feature selection and hyperparameter tuning

Feature selection is a process where the most relevant features in a data are automatically selected. Hyperparameter tuning is the process of selecting the optimal set of hyperparameters for a learning algorithm [209]. Evaluating a model means analyze how it will perform on the test dataset. For instance, ML data scientists train their models and compare how well it generalizes utilizing the test set. It is supposed that they selected the best model configuration, but now they must apply some regularization to avoid model overfitting. The main question is, how do they choose the value of the regularization hyperparameter? One option is to train models using different values for this hyperparameter, by running hyperparameter tuning. Most publications do not apply feature selection or processing and hyperparameter tuning to their models. Some only highlighted their feature selection [24,29,31,34,140], and others only tuned their model hyperparameters [38,40] or used default settings [25,102]. Studies considering both feature selection and hyperparameter tuning are rare [2,11,16,19]. The most used hyperparameter search approaches are the grid search method with cross-validation [21] or the random search method with cross-validation [36]. These all mean the research community could benefit from more comprehensive and systematic approaches to model refinement.

4.4. Ensemble techniques

Suppose a complex question presented to thousands of random persons, then their answers are collected. Generally, their collective answer is better than an answer from an expert. This is called the wisdom of the crowd. Similarly, if a material property is predicted by using a group of predictors (such as classifiers or regressors), often better predictions are carried out than the best individual predictor. A group of predictors is called an ensemble, and the technique is called ensemble learning. An ensemble learning algorithm is also called an ensemble technique. For example, Yan et al. [128] used 3 ensemble models to predict hardness of steel. A typical example of ensemble learning is RFs which perform better than individual decision trees [209]. RF is employed in a variety of alloy development research that is discussed later sections in this chapter.

4.5. Artificial neural network

ANNs are ML models inspired by biological neuron networks in our brains [209]. ANNs have gradually become quite different from their biological cousins. They are versatile, robust, and scalable, ideal for tackling large and highly complex ML tasks such as classifying billions of images, powering speech recognition services, or recommending the best videos to watch to hundreds of millions of daily users.

A massive quantity of data is nowadays available to train ANNs in different fields, and ANNs frequently outperform other ML techniques on vast and complex problems. The significant increase in computing power since the end of the 1990s and the beginning of the 2000s, also thanks to the gaming industry, which has stimulated producing powerful GPU cards, made it possible to train large ANNs in a reasonable amount of time [209].

A required large dataset, which most cases not available for particular materials or alloys, is one of the main theoretical limitations of ANNs. Also, many researchers thought that ANN training algorithms would likely get stuck in local optima. Still, this is not a big problem in practice, especially for more extensive ANNs: the local optima often perform almost as well as the global optimum [209]. ANNs had slow progress because of their complexity and lack of interpretability of their results. Nevertheless, this did not stop more attention toward them, resulting in more and more improvement and even more unique predictions.

It’s essential to note that, the terms ‘neural network’ (NN), ‘artificial neural network’ (ANN), and ‘deep neural network’ (DNN) are not used interchangeably in this research because it is important to use the terminology that accurately describes the type of network you are discussing.

4.6. Design and prediction of mechanical properties

Researchers used ML to enhance design of experiments including developing high-throughput rapid experimental alloy development [210], proposing a general experimental design [211], maximin and centroid design strategies [212], improving alloy design efficiency [213,214] and catalyst design [215].

Estimating the mechanical properties (e.g. Yield strength) of an indented material is often challenging. Conventional optimization techniques are generally unable to yield accurate values. Fernandez-Zelaia et al. [216] have proposed combining a Gaussian Process surrogate model using finite element models of spherical indentation, a Bayesian optimization and Markov Chain Monte Carlo sampling. The efficiency of the approach was tested against the experiment with good agreement. In a separate instance, ML models were applied to anticipate the tensile strength of metallic materials subjected to hydrogen exposure [217]. Additionally, ML was employed to classify stress hotspots in another case [218].

4.7. ML models and accuracy

In Figure 6, a sankey diagram illustrates the relationship between ML models and the alloys under study. Notably, NN, RF, and SVM, which are the most frequently employed ML models, are used to predict parameters across a diverse array of alloys. This indicates that researchers do not confine themselves to a particular ML model when investigating specific alloys. Notably, steel, HEA, aluminum, nickel, and range of alloys (researches that encompassing a range of alloys within a single paper), collectively account for 50% of the papers employing ML in alloy development. Furthermore, it is observed that 18% of steel research and 33% of aluminum research employ NN as their preferred ML model. The graphical representation underscores that researchers do not impose limitations on the choice of ML models for specific alloys, resulting in a relatively equitable distribution of models across the various alloys studied.

Figure 6. Sankey diagram with ML models on the left side and the studied alloys on the right side. The diagram is an illustration of the relationship between the ML model and predicted alloys.

Various ML models such as ANNs, SVMs, and decision trees have been applied to the alloy development process. These models can be used to predict the properties of an alloy based on an optimal composition for a given set of desired properties.

4.8. ML, first-principles, CALPHAD and thermodynamic approaches

Inputs derived from first-principles calculations [59,150] and thermodynamic modeling methods such as CALPHAD [210,213] have been heavily used in ML applications in alloy research. First, theoretical modeling can generate big data sets for ML models. Theoretical modeling calculations are heavy and slow for computing machines, while similar calculations of ML can be performed faster in similar computing machines. Secondly, traditional modeling methods can be used to validate the outcome of the ML models. Both advantages show how traditional modeling and ML can balance each other.

One approach to using ML in alloy development is first to gather a large dataset of alloy compositions and their related properties. This dataset can then be used to train an ML model, which can then be used to make predictions about the properties of new alloy compositions. The accuracy of the model can be improved by increasing the size and diversity of the training dataset and by hyperparameter tuning of the ML model.

Another approach is to use an evolutionary model, such as genetic models [196,197], to search for the optimal alloy composition. This approach generates relevant libraries. Therefore and evaluates an initial population of alloy compositions based on their predicted properties. The compositions that perform best are then used to generate a new population, which is again evaluated, and the process is repeated until the optimal composition is found.

4.9. The challenge to generate data

Research shows that the accuracy of ML models can differ even with the same data set [219–221]. Each ML model has its unique structure with underlying mathematical concepts and relevant libraries. Therefore, it is essential to identify the best-fit model by critically analyzing performance parameters before applying it to real-world scenarios. Such an approach in ML model selection is a promising methodology with minimal effort to discover novel alloy compositions compared to conventional alloy development procedures.

Results of the published papers show that the accuracy of ML models can differ even with the same data set. So, different accuracies are reported in a single article. Table 2 shows the pros and cons of using some of the ML models. Researchers are encouraged to make informed ML model selections by weighing these factors. Highlighting models that outperform their counterparts, this paper recommends top ML models for alloy development, with further discussion in the ‘ML Models and Accuracy’ section.

Table 2. Pros and cons of some of ML models [85,112,148,209,220].

ML model	Pros	Cons
Linear regression	Simple but efficient model	Linearity assumption and outlier effect
Polynomial regression	Less impact from the size of the database	Polynomial degree optimisation
Support vector regression with linear kernel	Efficient in high dimensional spaces, Memory efficient	High impact of noisy data- not suitable for large database
K-nearest neighbouring	No assumptions and simple model	K value optimisation cannot deal with missing values
Artificial neural network	Ability to work with incomplete data	Need higher processing capacity, complex behaviour.
Random Forest	Handles large number of training examples and high dimensional spaces well, No pre-processing required, Robust to outliers	Can overfit if there are noisy data, Difficult to interpret
Support Vector Machine	Works well in high dimensional spaces, Fast prediction, Memory efficient	Not suitable for large datasets, Sensitive to noisy data with overlapping classes, Requires feature vectors
XGBoost	Highly customizable, Works well with large datasets, Handles missing values efficiently	Cannot handle categorical features, More memory-hungry than some other models, Can be slower than some other models

4.10. High throughput approach

In total, 28 of the studied papers used high throughput methods, e.g [102]. used High Throughput CALPHAD approach [187], and [189] used high throughput ab initio method, and [69] used high throughput molecular dynamics, the rest of the papers studied experimental High Throughput methods. While U.S.A. and China are the frontiers in using High Throughput, Carrete, et al. in France are using the method to predict the physical properties of Half-Heusler [187–189]. It is important to highlight that in High Throughput studies, RF, SVM, and XGBoost have consistently emerged as the ML models with the highest reported accuracy. Interestingly, even though the high throughput approach is employed to generate extensive data in materials science, NN have not been widely utilized for modeling this type of data. This stands in contrast to the broader field of alloy development, where on average, NNs have been the researchers’ preferred choice for ML applications.

4.11. Computer vision in image processing

Computer vision and Convolutional neural networks (CNNs) emerged to solve problems related to visual tasks. Power image search services, self-driving cars, and automatic video classification systems are among their applications and more [209].

By using image processing techniques, researchers can analyze the microstructure of alloys at various scales, from the atomic to the macroscopic levels. A small portion of the studied publications used image processing in alloy exploration and development [29,58,125,184,222]. Image processing is mainly used for microstructure evaluation, such as identifying stress hot spots [184].

4.12. The challenge to find the best ML approach

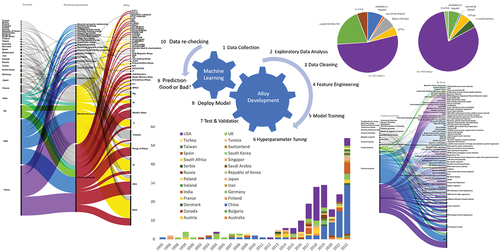
The Pie chart of Figure 7 reveals that the majority of publications (68%) rely on a single ML model for their research while others used more than one ML model to predict parameters. It is notable that one publication authored by C. Wen et al. [79] stands out as an exception, employing an extensive array of 12 ML models in a single research paper. The remaining publications utilize a varying number of ML models, ranging from 2 to 11, demonstrating diversity in the approaches taken by researchers in selecting and applying ML models to their work. This is showing at least 32% of the researchers may have encountered uncertainty or difficulty in determining one ML model as the most appropriate model for their specific application.

Figure 7. The pie chart illustrates the frequency of ML model usage within a single published paper. For example, one paper used 12 ML models in one published paper while the majority of papers used only one ML model.

Following uncertainty for the best ML model for the application, researchers compare the results from every ML model to find the best. Figure 7 shows the frequency of using other ML models in every publication. This statistical result reflects the popularity of the ML models and not necessarily the accuracy of the predictions or the advantage of using two or more ML models. Those researchers who used more than 1 ML model compared the accuracy of the models and presented their best ML model. A review of the best suggested ML models presented earlier in 4.7, ML models and accuracy.

As previously discussed, some researchers adopted a multi-model approach to identify the most accurate solution for their specific applications within the realm of ML. They conducted assessments of accuracy and reported their findings, while others chose not to share accuracy information [110]. Figure 8 shows predicted parameters and their correspondent best-reported ML models. The connections between the predicted properties and ML models reveal which ML model was reported as the best performer for predicting a particular alloy property. For instance, if mechanical property is connected to RF, it suggests that RF was found to be the best ML model for predicting mechanical properties. The suggested model was selected the best in comparison with the other models that used in the same paper. The graph is extracted only from the papers that used more than one ML model, compared those models and reported the best. RF, SVM, XGBoost, and SVR are introduced as the best ML models for all the predicted parameters. It is interesting to learn that while NN is the most used ML model (section 4.1 Predicted Parameters), however among more than 200 studied papers, just two researchers reported NN as the best ML model [18,140]. Furthermore, it is noteworthy that 12 distinct ML models were reported as the best for predicting mechanical properties, and 7 ML models excelled in predicting physical properties. With one exception, the ML models ideal for predicting mechanical properties were not the same as those for predicting physical properties.

Figure 8. Sankey diagram with predicted parameters on the left side and the best-suggested ML models on the right side. The diagram is an illustration of the relationship between the predicted property and the alloy of the best-suggested ML model for predicted properties. This graph is not showing all of the studied papers. It is only showing the results of those papers that compared different ML models and reported the best ML model.

5. ML deployment

Suppose a model is launched into production, but unfortunately, it does not perform as well as expected and produces large errors. The problem lies in the fact that the generalization error was measured multiple times on the test set, and the model and hyperparameters were adapted to yield the best model for that dataset. This means the model is unlikely to perform as well on new data. Therefore, ML deployment task is often missed or ignored in the journey of building the model in the vast majority of the ML publications. Figure 9 illustrates how data flow is used to improve alloy development. The data flow begins with data collection and concludes with data re-examination and re-assessment. This data flow aids researchers in enhancing their processes by reviewing the steps.

Figure 9. Building a data flywheel for ML modelling: (1) data collection, (2) Exploratory Data Analysis (EDA), (3) data cleaning/preprocessing, (4) feature engineering, (5) training an ML model, (6) optimization through hyperparameter tuning, (7) testing and validation of the best ML model, (8) Model deployment for production, (9) evaluation of the accuracy and the quality of final predictions, (10) data re-checking and re-evaluation. Steps 8–10 are usually missed or neglected in most of the published works.

To deploy ML algorithms, it is possible to use a cloud-based environment (e.g. AWS, Google Cloud and Microsoft Azure) to train, deploy, automate, manage, and track ML models. It is often used with cloud storage where potentially large amounts of data are also considered in the ML process. Using cloud-base environment is not expanded in this research because it is not used by majority of the researchers in field of alloy development.

6. Data and code availability

It is crucial to present the primary data used to construct ML models as it enables other researchers to reproduce the results and validate the findings. This practice also ensures that the data utilized in the model is precise and impartial. Moreover, it allows other researchers to reproduce the results, build upon the work, and develop novel models based on the same data. Figure 10(a) shows the availability of the primary dataset in the studied publications. In some cases, the dataset was presented in the text [180], some in a supplementary file [7], in some cases, an external link [166] was given; some said it would be available on request [67], some said they could not share the data [57] and some referred to their github.com repository [21]. This is while most of the researchers did not present the primary dataset at all. This research shows that recent publications have more tendency to share their dataset. It should be mentioned that sharing the dataset and code in some journals is mandatory.

Figure 10. Pie charts showing (a) data availability and (b) code availability, in the studied publications. The figures provide insights into how often data and code are shared within the research community have implications for the transparency and reproducibility of the research.

Sharing the code of ML models is crucial as it enables other researchers to reproduce the results and validate the findings. This practice also ensures that the code utilized in the model is precise and impartial. Moreover, it allows other researchers to build upon the work and develop novel models based on the same code. Figure 10(b) shows abundance of publications that shared the code of their ML model. Surprisingly, 81% of the researchers did not share their code while 14% said the code will be available on request.

7. Conclusion and outlook

In recent years, ML approaches have gained significant attention in alloy development. This statistical literature review highlighted advanced ML methods used in alloy design worldwide, where the U.S.A. and China are the leading countries in the selected publications.

It is found that steel, HEA, and aluminum were the most extensively studied alloys in the field. Investigators from the U.S.A. have extensively examined a range of alloys, while researchers of other nations mostly focused on a single alloy system in one publication.

Computational Materials Science is the journal with the highest publication rate in the field, with 10% of the published papers.

The use of ML approaches in predicting physical, mechanical, and catalytic properties in several alloys ranging from light and HEA to amorphous, Ni-based alloys and steels were thoroughly. The fact that researchers explored and utilized a wide spectrum of ML tools and approaches to improve and advance the development of alloys is indicating the versatility and comprehensiveness of their approach. This research indicates that the U.S.A. leads in diverse alloy property prediction using ML compared to other countries.

This comprehensive analysis underscores the diverse ML models adopted in property prediction and reveals a desire of researchers for NN, RF, and SVM that collectively representing 20% of all models employed. These models are used to predict parameters across a diverse array of alloys. This suggests that researchers do not limit their research to a specific ML model when studying a particular alloy. So, the models distributed equally for the alloys.

Researchers display a wide range of preferences when it comes to ML models, and while some models are tailored for specific tasks, others, such as Linear Regression, are seen as having distinct applications by researchers.

This research shows most publications neglect feature selection, hyperparameter tuning, or both. Only a few studies address both aspects, primarily employing grid or random search methods with cross-validation. The materials’ research community could benefit from more comprehensive and systematic approaches to model refinement.

The dataset size and structure essential to the model accuracy were discussed. Most used ML approaches, such as ensemble techniques, NNs, and computer image processing, were also revisited. Those which underwent careful feature selection and hyperparameter tuning and reported the best optimal models were highlighted. Often available data useful for alloy property prediction is too small, with few features. This creates a challenge of generating the extra necessary data from other resources, such as first-principles calculations and thermodynamic approaches, which can benefit some studies.

It is worth noting that 68% of the publications used only one ML model, 9% used two ML models, and the maximum number of ML models used in a single paper was 12. Most used ML models were in the following order: NN, RF, SVM, SVR, Gaussian process, and Linear Regression.

While NN is the most used ML model, only two papers presented NN as the best model, in comparison with the other models. Notably, the ML models that had been the best for predicting mechanical properties were not the same as those for predicting physical properties.

Linear regression and XGBoost were the most frequently used models for predicting mechanical properties, while the Gaussian process and Bayesian optimizations were the preferred models for predicting physical properties. Steel, aluminum, and titanium were the most studied alloys in terms of their mechanical properties, whereas in the case of HEA and metallic glasses, the focus of the studies was on their physical properties.

Researchers reported that ensemble techniques with SVM provided the highest accuracy in predicting the properties of alloys, while NN was the most used model. High Throughput methods were used in 12% of the publications. It is alarming that 53% of the publications did not share their datasets, and 81% did not share the code used to build their ML models. So, sharing datasets and codes used to build and deploy ML models should be encouraged to promote reproducibility and facilitate future research in this field. Also, only 2% of the publications used image-processing techniques for alloy development.

Overcoming obstacles requires standardization, enhanced collaboration, and innovative algorithms that can handle the complexities of alloy systems. Continuous interdisciplinary collaboration will be vital in pushing the boundaries of what is possible, ensuring that the insights gained from computational methods are effectively translated into real-world applications.

This research demonstrated how standardization is the lost part of using ML in alloy development research. Standardized formats and protocols for data collection, storage, and sharing make it easier to combine datasets from various sources including experiment and CALPHAD results. Standardization can help ensure data quality and consistency. It provides guidelines for data validation, calibration, and error correction, reducing the chances of erroneous results. This statistical literature review has aimed to compare models, but it becomes evident that the best benchmarking can only be achieved through the use of standardized datasets and evaluation metrics, enabling equitable model comparisons and performance assessments among peers.

Authorship contribution statement

Alireza Valizadeh: Investigation, Data curation, Conceptualization, Methodology, Writing – original draft, Visualization, Writing – review & editing. Ryoji Sahara: Conceptualization, Writing – review & editing. Maaouia Souissi: Investigation, Conceptualization, Methodology, Writing – original draft, Supervision, Project administration, Writing – review & editing.

Acknowledgements

We acknowledge Dr Taylor D.Sparks from The University of Utah for many useful discussions.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Notes on contributors

Alireza Valizadeh

Alireza Valizadeh, is a distinguished scientist in materials informatics, and specializes in energy materials. With a Ph.D. from Brunel University London, he currently researches at NEX Power Ltd, utilizing AI and machine learning for materials development. Focused on the energy sector, his goal is to innovate sustainable energy solutions. In 2018, he was awarded the Frank Fitzgerald medal by the Institute of Materials, Mines and Minerals for his extensive work in the iron and steel industry. Through his pursuit of scientific excellence, Alireza shapes a sustainable energy landscape for societal and environmental benefits.

Ryoji Sahara

Ryoji Sahara, graduated in Materials Science from Tohoku University, Japan, in 2000. He worked as an assistant professor at the Institute for Materials Research (IMR) and later joined the National Institute for Materials Science (NIMS) as a principal researcher in 2003. At NIMS, he supervised postdoctoral researchers, leading projects on carbide formation in heat-resistant creep steels, oxidation of titanium alloys, and materials design using machine learning. He collaborates with researchers from Saveetha University, TU-Deft, and Ohio State University. As chairman and member of ACCMS, he contributes to computational materials science. With 60+ publications, he currently leads the Computational Structural Materials Group at NIMS’s Research Center for Structural Materials.

Maaouia Souissi

Maaouia Souissi, graduated from the National School of Engineering of Sfax in 2005 and worked as a research assistant in Tunisia until 2007. He obtained his Ph.D. in Materials Science from Tohoku University, Japan, in 2011. Following that, he conducted postdoctoral research at Osaka Prefecture University for five years, focusing on defect modeling in steels using density functional theory. In 2016, he joined NIMS, Japan, investigating structural materials modeling for high-strength heat-resistant applications. Later, he joined Brunel University London as a research fellow, collaborating with Constellium partnership on aluminum alloy development for aerospace and automotive purposes. He has over 15 years of research experience, contributed to prestigious journals, and actively participated in international conferences.