Impossibilities without impossibilia

ABSTRACT

Circumstantialists already have a logical semantics for impossibilities. They expand their logical space of possible worlds by adding impossible worlds. These are impossible circumstances serving as indices of evaluation, at which impossibilities are true. A variant of circumstantialism, namely modal Meinongianism (noneism), adds impossible objects as well. These are so-called incomplete objects that are necessarily non-existent. The opposite of circumstantialism, namely structuralism, has some catching-up to do. What might a structuralist logical semantics for impossibilities without impossibilia look like? This paper makes a structuralist counterproposal. We present a semantics based on a procedural interpretation of the typed λ-calculus. The fundamental idea is that talk about impossibilities should be construed in terms of procedures: some yield as their product a condition that could not possibly have a satisfier, while the rest fail to yield a product altogether. Dispensing with a ‘bottom’ of impossibilia requires instead a ‘top’ consisting of structured hyperintensions, intensions, intensions defining other intensions, a typed universe, and dual (de dicto and de re) predication. We explain how the theory works by going through several examples.

KEYWORDS:

• Impossibility
• predication
• structuralism
• circumstantialism
• modal Meinongianism
• Transparent Intensional Logic

1. Introduction

The aim of this paper is to put forward a structuralist counterproposal to the dominant circumstantialist account of impossibility.¹ Circumstantialism belongs to model-theoretic semantics and needs circumstances that can serve as points of evaluation, at which propositions are evaluated. This motivates adding impossible worlds to the logical space. Evaluation presupposes the predication of properties of objects at impossible worlds. This enables predicating properties (including ones that could not possibly have an instance) of impossible objects such as round squares or divorced bachelors. Circumstantialism makes it feasible to stick to the well-entrenched world idiom in semantics. Model-theoretic semantics centres around truth-conditions and so is born intensional. The hyperintensions of circumstantialism are generated by means of mappings defined on an expanded logical space. Adding impossible worlds to logical space enables circumstantialism to go hyperintensional. Any two formulae that are equivalent across all possible worlds still have distinct truth-conditions, because these two formulae have different distributions of truth-values across the impossible worlds.

Structuralism introduces structured hyperintensional entities sui generis straight away and so is inherently hyperintensional. This explains why structuralism does not invoke impossible worlds, nor predicates properties of impossible objects. Impossible objects are not construed as objects that are impossible. Rather, impossible objects are accounted for by way of abstract logical structures that are structured (and in some theories also typed) to yield an object with such-and-such incompatible properties. Impossible objects are elevated, as it were, to concepts, with structures playing the role of concepts. This reorientation makes for a concept-first (structure-first) and top-down approach of an extreme kind, because there is no backward path from objects to concepts simply for want of impossible objects. Dispensing with a heavy bottom of impossibilia requires instead a heavy top containing, at least, structured hyperintensions, intensions, and dual (de dicto versus de re) predication, with a typed universe as an option to keep track of what is going on within the structures and between top and bottom. The resulting structuralist account of impossibilities turns out to be an account of a particular cluster of limiting cases within an overall structuralist framework. Worlds are indispensable, because extreme intensions (functions from worlds) are indispensable, although also insufficient, because the account of impossibility is cast in terms of structures.

The focus in this paper is on how predication works in the case of impossibility. Getting a handle on predication is crucial for how inference from instances of ‘impossible predication’ works. The reference to inference serves to motivate an inquiry into the conceptually prior notion of predication. More specifically, what we are putting forward is an outline of a structuralist semantics for impossible predication. The semantics for impossible predication falls out of an existing theory that has already been applied and tested across a wide range of topics, and the semantics involves no ad hoc epicycles or novel entities.

The rest of the paper is structured as follows. Section 2 provides background for the clash between circumstantialism and structuralism, and summarises the relevant portions of a Meinongian variant of circumstantialism. Sections 3 through 5 explain the philosophy of a procedural variant of structuralism, defines its fundamental notions, and goes through a number of examples.

2. Impossible predication and Meinongian circumstantialism

First, we describe the problem of impossible predication, which both circumstantialism and structuralism address. Then we turn to circumstantialism and the problems we have with it.

It is an analytic triviality that impossible objects could not possibly exist. But then how could a property be predicated of an impossible object? This is the problem of ‘impossible predication’. It is understood that when, contingently, the King of France fails to exist there is no appropriate individual of whom to predicate that he is bald. It is also understood that there are alternative worlds equipped with a unique King of France, and that he can be predicated to be bald. Any such individual is denoted by ‘a’ in the makeshift schema Pred (F, a). A subset of worlds each has a unique King of France, and a subset of that subset is such that its world-relative Kings of France are bald. But Pred (F, a) fails for impossible objects, unless one settles for the puny result that Pred (F, a) invariably turns out false or else gappy (devoid of a truth-value), depending on one’s overall theory. This puny result is incapable of accommodating valid inferences such as: ${\displaystyle \frac{\mathrm{The}\mathrm{round}\mathrm{square}\mathrm{is}\mathrm{round}\mathrm{and}\mathrm{square}}{\mathrm{There}\mathrm{is}\mathrm{something}\mathrm{that}\mathrm{is}\mathrm{identical}\mathrm{to}\mathrm{the}\mathrm{round}\mathrm{square}}}$ ${\displaystyle \frac{\mathrm{The}\mathrm{round}\mathrm{square}\mathrm{is}\mathrm{round}\mathrm{and}\mathrm{square}}{\mathrm{There}\mathrm{is}\mathrm{something}\mathrm{that}\mathrm{is}\mathrm{both}\mathrm{round}\mathrm{and}\mathrm{square}}}$We are treating the above inferences as data to be accommodated, and extract from these data the explanandum how predication works for the respective premises and conclusions. We will take it to be a philosophical desideratum that such inferences not be degenerate cases of truth-conditional vacuity, as with material conditionals whose antecedent is a necessary falsehood. We will also take it to be a philosophical desideratum that it must not be arbitrary what can be validly inferred from a categorical (as opposed to conditional) proposition. Thus, we are not going to invoke ex falso quodlibet.

Next, we outline a Meinongian variant of circumstantialism. Whereas alethic impossibility may be harder to get one’s head around pace dialetheists, doxastic impossibility (‘believing the impossible’) should be common fare.² Within the model-theoretic world idiom, the standard axioms for belief (i.e. the doxastic interpretation of □) is KD45 (i.e. distribution, seriality, positive and negative introspection). A proposition α believed to be true need not be true at the world, at which the belief is entertained, but it must be true at some world accessible from that world, which entails that α must be logically consistent:

Axiom (D) is valid on serial frames: ∀w∃w′(Rww′). Being possibly true is a necessary condition for possibly being believed. This requirement rules out believing necessary falsehoods, i.e. impossibilities. This is a case of a formal framework dictating what is philosophically feasible, which gets the priorities back to front. A strong philosophical case, pace Hume, can be made for the existence (and not just the theoretical possibility) of ‘impossible beliefs’. (For instance, Frege thought that Basic Law V was consistent.) Modelling them requires preserving seriality. The consequent requires the existence of a world, at which α is true. The Meinongian circumstantialist move is to introduce a second logical space, one populated with impossible worlds, and conjoin it with the original logical space of possible worlds: W∪IW. A proposition α is now identified with the set of possible and impossible worlds, at which it is the case that α. The benefit is that there is an (accessible) impossible world w′′, a point of evaluation, at which α is true: ∃w′′(α_w′′). The situation is now that believer a believes α at w∈W, a world at which α could not possibly be true, though fortunately α is true at w′′∈ IW. Axiom D still stands as a formal feature of belief, and ‘impossible beliefs’ have become an option.

The price exacted is the adoption of impossible worlds to provide additional circumstances. (In the following paragraph, we explain why we consider this price too high.) Impossible worlds remain problematic, even when taken onboard as mere theoretical artefacts exclusively for the purposes of capturing the right inferences. They are equally problematic, we think, regardless of whether the modality is alethic or doxastic, i.e. never mind whether ‘woodchucks might not be groundhogs’, ‘π might have a final decimal’, ‘fallen angels might not have been angels’, etc., are construed as expressing alethic or doxastic possibilities. We share the standard view that alethic possibility requires an objective potential or capacity in a given (kind of) object, while doxastic possibility requires an agent’s intellectual capacity to combine concepts in a particular way (unencumbered by logical inconsistency). Epistemic possibility, then, is predicated on an agent’s ignorance: for all (the little) an agent knows, such-and-such is epistemically possible for the agent, i.e. the agent’s knowledge is not strong enough to eliminate such-and-such as not being epistemically possibly true.

Here are the three problems we have with impossible worlds. First, impossibilia are being assumed straightaway by frontloading impossible worlds in the account of impossibility. The availability of impossible worlds enables the circumstantialist to remain squarely within model-theoretic semantics, equating sentential meaning with truth-conditions, and maintaining an extensional or denotational theory of singular terms, predicates, etc. It is an option to include not only ‘℩xφ’ but also ‘ϵxφ’, the latter earmarked for arbitrary reference: given an equivalence class of objects, of whom or which φ is true, a specific member is randomly selected and made the referent of ‘ϵxφ’.³ This position combines a conservative, almost reactionary choice of framework with a bold expansion of one’s (formal) ontology.⁴ However, an impossibility is modelled as something that occurs at an impossible world. This is potentially circular, and viciously so. Of course, a circumstantialist rejoinder may be that this is no worse than modelling a possibility as something that occurs at a possible world.⁵ The circumstantialist may add that their straightforward semantics can model talk about impossibility at face value (e.g. when apparently talking about an impossible object, then there is, in a noneist manner, an impossible object that is being talked about being available for predication), whereas the structuralist will need to reinterpret talk about impossibility, apparent reference to impossible objects, etc.

Second, circumstantialism trades in impossible objects. This point must be phrased carefully, though. If a constant domain for the union of possible and impossible worlds is assumed, then actual (hence possible) objects will be instantiating impossible properties at impossible worlds. (You, for instance, get a go at being a divorced bachelor, a triangular pentagon, etc.) But when it is true at w′′∈ IW that you are a divorced bachelor who is a triangular pentagon, then you are, at w′′, an impossible object. This is required, because predication needs to be predication de re for the Meinongian circumstantialist.⁶ However, it is not a very helpful explanation of ‘impossible predication’ to be told that this or that actual individual has this or that impossible property at some impossible world. The real issue, we contend, is with the property and its very inability to be instantiated at any possible world, not with it being applied to a hapless individual at an impossible world. Thus, we are inferring the impossibility of predication de re from the impossibility of instantiation. The Meinongian indifference as to who or what the subject of predication is, is reflected by the fact that the subject is selected randomly (because, why not, the predication is impossible, anyway). Alternatively, by adopting varying domains, one can have not only non-actual but impossible individuals populate the domains of impossible worlds. Going for varying domains, however, only perpetuates the problems besetting varying-domain semantics for possible worlds. How are we to identify and individuate non-actual individuals, now that ostension and other non-qualitative ways of identification and individuation are not an option? We will need descriptive material for this, but if the descriptive material is indispensable, then why not discard these presumed individuals and make do with the descriptive material? This move shifts the weight from extensional onto intensional entities.⁷

Third, circumstantialism fails to distinguish between intension-involving and non-intension-involving, or empirical and non-empirical, impossibilities. For instance, in circumstantialism there is an impossible world, at which e is rational, another where the Euler identity fails to hold, yet another at which denying the antecedent is a valid inference, and still some other where trilateral pentagons abound. But are mathematics and logic a worldly matter? Does it even make sense to say that the sum of 7 and 5 is 12 at the actual, hence some possible, world? To make sense of this, numbers will have to be assigned to domains of worlds. And more generally, domains will have to be populated with logical and mathematical entities. We struggle to understand this idea, especially when these abstract entities are supposed to have different properties at different impossible worlds. We understand that magnitudes are worldly matters, like the temperature in the room being 25⁰. But magnitudes are numbers-in-intension: functions from worlds to numbers. We prefer to reserve worlds for empirical contingencies, using different points of evaluation to bring out different functional values, such as satisfaction classes, truth-values, etc., which is the contrast between the actual and the merely possible. Necessity and impossibility are limiting cases that gain nothing, in point of explanation, from the variability between different values at different worlds that contingencies do. The structuralist alternative does not evaluate Euclidean geometry, elliptic geometry, hyperbolic geometry, etc., at worlds. This does not exclude applying one or the other geometry to possible worlds. This clears the path for measuring, say, triangles, the sum of whose angles is at most, at least, etc., 180⁰. This sort of application makes sense when exploring worlds whose laws of nature are such that, say, parallel lines do converge at one end and diverge at the other. When nomological necessity is ‘soft’, nomologically impossible worlds (i.e. worlds whose laws are not those of the actual world or any other world nomologically indistinguishable from it) are still logically possible worlds.⁸ The adjacent geometry defines for any such subset of logical space what a triangle is, what parallel lines are, etc. For instance, a set of laws of nature may come with a notion of space that is incompatible with Euclidean geometry; instead, space is a sphere structure that is compatible with elliptic geometry, or space is a saddle structure that is compatible with hyperbolic geometry. Still, any intensions required to model equivalence classes of laws of nature will be defined on possible worlds only.

These three objections converge in the overall objection that circumstantialism misconstrues impossibility philosophically.⁹ As we see it, an impossibility is not something that could not possibly exist. Impossible-world semantics treats impossibilia as actual relative to some impossible world, hence as possible relative to a subset of logical space. Hence, an impossibility is, technically speaking, a contingency, something which occurs at some but not all worlds in IW. This Meinongian construal does not take it seriously enough that an impossibility is nothing. Our philosophical objection is that the world idiom is guilty of imperial overstretch, because it misconstrues impossibility as possibility in an alternative logical universe.¹⁰ If instead no domain of any world contains impossible objects, predication de re is ruled out as an option. Our conclusion is that a bottom-up, object-based account of impossibility is philosophically flawed.

3. The philosophy of procedural structuralism

When insisting that there are no impossibilities (no impossibilia), even in a non-committal noneist manner, simply because there could not possibly be any, we are not explaining impossibility away. Rather we are shifting the weight away from impossibilia and onto procedures that are structured and typed to produce an entity of a particular type and with a particular blend of properties. Hence, an impossible object is not an object at all, but the impossible (hence, necessarily absent) product of a procedure structured and typed in a particular way. There is no such object anywhere in logical space. There is, instead, the abstract construction, or mode of presentation, of such an object: a procedure together with a logical type and a condition. In our view, the modifier impossible has a privative effect on its argument property, whereby an impossible X is not an X that is impossible, but no X at all.¹¹ Thus, for instance, the only way we can make sense of the notion of an impossible world is as a condition that no possible world could possibly satisfy. It is this sort of ascent from the objectual to the conceptual that we want to make formally explicit below.¹²

Our structuralist counterproposal is developed within Transparent Intensional Logic (TIL). The ontological commitments of TIL are its typed universe, in which each entity is either a procedure or a function (including medadic ones like individuals and truth-values). The types are doing much of the heavy lifting. While there is no object such as a Russell barber or a last decimal of the expansion of π, there are the types of such objects. The logical machinery is hardwired to yield structured procedures that detail the procedure of, for instance, a property being predicated of an object of whatever type. Hence, the logical type of a in ⁣ Pred (F, a) needs to be radically reconsidered. We are mindful not to be stuck with instances of predication that would be a nexus between type-theoretically incongruent entities, as when predicating the property of wearing a wig of an individual-in-intension.¹³ Of course, just that may be what is wanted, and we can model it, but more likely the analysandum is something like ‘The local Russell barber wears a wig’, which is what we typically need to capture formally.

TIL is erected on a procedural interpretation of the typed λ-calculus. The various sorts of λ-terms denote various sorts of procedures; they do not denote or otherwise represent mappings or values of mappings. Procedures are algorithmically structured, higher-order objects that are conceptually prior to execution, if any.¹⁴ Some of them are impossible to successfully execute, yet still detail a specific intellectual itinerary. Some procedures yield a product, others do not and are in this sense ‘roads to nowhere’, itineraries without a destination. The underlying philosophy is ante rem Platonism.

Two complex, or multi-step, procedures are the ones of functional abstraction, which specifies how to generate a function, and functional application, which specifies how to obtain the value, if any, of a function at an argument. Two simple, or one-step, procedures provide the complex procedures with (specific or arbitrary) entities of a specific type to work on. The entire ontology is organised within a ramified type hierarchy. The ontology encompasses extensional entities such as individuals, truth-values and sets, intensional entities (mappings from possible worlds) such as individual concepts or individuals-in-intension (e.g. the largest desert on Earth), empirical truth-conditions and empirical properties, and hyperintensional entities, which are procedures. For instance, the procedure prescribing the application of the factorial function to 5 and the procedure prescribing the multiplication of 60 by 2 are two distinct procedures that converge in the same product, the number 120. The product is never a constituent of any procedure producing it.

The overarching idea is that impossibilities should be analyzed by means of fine-grained procedures accompanied by type specifications. The types specify the respective types of the respective entities involved, and the procedures specify the logical interaction between these entities. A procedure is structured and typed to produce an entity of a particular type. For instance, the procedure specifying the application of the addition function (taking pairs of numbers to a number) to the pair (7, 5) is structured and typed to produce a number, which is the sum of (7, 5). As a limiting case, a procedure typed to produce an entity fails to produce a product. For instance, no procedure structured and typed to produce the integer between 1 and 2 will produce anything. Turning up empty-handed never happens with an instance of the procedure of functional abstraction, including one typed to produce an intensional entity. At the limit, the product is going to be a degenerate function, which is not much, but still something. Either the function returns no value at any argument, or the function returns invariably the truth-value F. Note that sets and relations are identified with their characteristic functions, so sets and relations are typed to yield truth-values.

The fundamental bifurcation among ‘impossible’ procedures is between those that could not possibly produce a product, and those that do produce a product, though a degenerate or negative one. It may be helpful to think of intensions as conditions.¹⁵ Some intension-producing procedures produce as their product a condition that could not possibly have a satisfier. These are the procedures we are interested in. Here is how these procedures fit into the overall architecture. The typed universe yields a tripartite structure with procedures at the top, intensions in the middle and extensions at the bottom. Two things to note. One is that these intensions are invariably going to be degenerate, or constant, or undefined throughout logical space. This explains why an account of impossibility exclusively in terms of intensions would be unhelpfully crude. Hence, logical space is not really where the action is when it comes to impossibilities.¹⁶ The other is that the extensional entities, if any, are even less significant than the intensions above them. Constant values like an empty set or F, or gaps throughout, serve only to make the intensions degenerate, etc. Lacking satisfiers throughout logical space reflects the fact that these intensions are impossible conditions. Procedures are foisted upon them, both in order to fine-grain impossibilities and to provide what we consider a philosophically more accurate theory of impossibilities.

To exemplify the bifurcation between extension-producing and intension-producing procedures, ‘is a woodchuck that is not a groundhog’ is a predicate whose meaning is a procedure that generates the impossible empirical property typed to be satisfied by individuals. Every empirical index will return the empty set of individuals, but there are infinitely many distinct procedures that generate the function from empirical indices to the empty set of individuals. More factors are involved in an intension-producing procedure than an extension-producing procedure. The definite description ‘the final decimal in the expansion of π’ has as its meaning a procedure that cannot generate a number. Still, there are infinitely many distinct procedures structured and typed to generate an entity of a particular type (here, the type of natural numbers) that fail to produce one. The difference between the two kinds of procedure is whether we descend from the hyperintensional through the intensional to the extensional level, or descend straight from the hyperintensional to the extensional level. Thus, the predicament for a procedure that conceptualises the largest prime number is that it bypasses the intensional level of constant functions and fails to pick up a satisfier at the extensional level. Therefore, notions like the largest prime number put extra pressure on one’s realm of hyperintensions, because hyperintensions are all we can have recourse to.

4. Foundations of Transparent Intensional Logic

Below follows an exposition of the fundamental definitions and technical notions we need for the purposes of developing the TIL theory of impossibility, accompanied by short explanations.

4.1. Procedures

Selected from the inductive definition of procedure, these five are the procedures we need for present purposes.

Definition 1 (procedure).

1. Variables x, y, … are procedures that produce objects (elements of their respective ranges) dependently on a valuation v; they v-produce.

2. Where X is an object whatsoever (an extension, an intension or a procedure), ⁰X is the procedure Trivialisation. ⁰X produces X without any change of X.

3. Double Execution, ²X, is the following procedure. Let X be any entity; the Double Execution ²X is v-improper (yielding nothing relative to v) if X is not itself a procedure, or if X does not v-produce a procedure, or if X v-produces a v-improper procedure. Otherwise, let X v-produce a procedure X’ and X’ v-produce an entity Y. Then ²X v-produces Y.

4. Let X, Y₁, … , Y_n be arbitrary procedures. Then Composition [X Y₁ … Y_n] is the following procedure. For any valuation v, the Composition [X Y₁ … Y_n] is v-improper if at least one of the procedures X, Y₁, … , Y_n is v-improper by failing to v-produce anything, or if X does not v-produce a function that is defined at the n-tuple of objects v-produced by Y₁, … ,Y_n. If X does v-produce such a function, then [X Y₁ … Y_n] v-produces the value of this function at the n-tuple.

5. The (λ-) Closure [λx₁ … x_m Y] is the following procedure. Let x₁, x₂, … , x_m be pair-wise distinct variables and Y a procedure. Then [λx₁ … x_m Y] v-produces the function f that takes any members B₁, … , B_m of the respective ranges of the variables x₁, … , x_m into the object (if any) that is v(B₁/x₁, … ,B_m/x_m)-produced by Y, where v(B₁/x₁, … , B_m/x_m) is like v except for assigning B₁ to x₁, … , B_m to x_m.

6. Nothing is a procedure, unless it so follows from (i) through (v). □

Remark. While Composition is the very procedure of functional application, Closure is the very procedure of functional abstraction. Even when a procedure is improper, as may happen with a Composition, the type of the entity the procedure is typed to produce can still be read off of the procedure in question.

Remark. There are two different sources of improperness. One is that a function f, though having an argument a, returns no value at a; that is, f(a) is a blank. The other is that f receives no argument a and so cannot return a value at a; that is, f trades a blank for a blank. This happens when a sub-procedure (see Def. 3 below) of a Composition C is improper, causing C to be improper. Still, the very procedure of functional application remains intact, even though on such occasions the procedure cannot be successfully executed so as to produce a product.

Remark. Trivialisation serves two purposes. First, it supplies non-procedures as objects to operate on. Every constituent of a molecular procedure is itself a procedure: Mont Blanc cannot occur within a procedure; ⁰Mont_Blanc can. Thus, if we want to specify the application of a function to Mont Blanc as an argument, a Composition must contain ⁰Mont_Blanc as a constituent sub-procedure. Second, Trivialisation serves to display other procedures.

Remark. Procedures can occur in one of two modes, displayed or executed. This distinction makes for a difference in logical form. A procedure occurring displayed occurs as the procedure it is, displaying what its constituents are, which types of entities they produce and how they interact so as to form a whole. A procedure occurring displayed does not descend to the level of a procedure occurring executed.

The ability to display procedures makes it feasible for a procedure to occur as a functional argument. This feature is what helps TIL to a logic of hyperintensional attitudes, as procedures (hyperintensions) can now appear as the second argument of an attitude relation. It likewise makes it possible to predicate properties of procedures. For instance, being improper, i.e. lacking a product, is a property of procedures that is central to our account of impossibility. The default mode for a procedure to occur in is as executed, which explains why it must be indicated, both conceptually and in the ideography, when a procedure occurs displayed. Occurring in executed mode means that the procedure specifies the descent from the procedure to its product: the object to be operated on in the following step(s) is the product and not the procedure. (There is an analogy between the descent from procedure to product, namely the intensional descent, or extensionalization, from intension to extension.) It is an additional issue whether a procedure occurring in executed mode can be successfully executed. Still, improper procedures can be executed, only not successfully so, because the execution yields nothing. What one can do, whether the procedure is proper or improper, is run a type check to figure out the type of the object the procedure is structured and typed to produce. Alternatively, a type check can reveal that a procedure occurring executed is ill-typed. In this case the execution will abort at some point, as when a function requiring α-typed arguments is offered a β-typed argument instead. A typical mistake would be attempting, in vain, to apply the extension of a property directly to an individual-in-intension, witness the example of the King of France and wearing a wig.

4.2. Intensions and extensions: first-order entities

Definition 2 (simple type).

Let B be a base, where a base is a collection of pair-wise disjoint, non-empty sets. Then:

1. Every member of B is an elementary type of order 1 over B.

2. Let α, β₁, … , β_m (m > 0) be types of order 1 over B. Then the collection (α β_1 …β_m) of all m-ary partial mappings from β₁ × … × β_m into α is a functional type of order 1 over B.

3. Nothing is a type of order 1 over B unless it so follows from (i) and (ii). □

For the purposes of natural-language analysis, we are currently assuming the following base of ground types, which form part of the ontological commitments of TIL:

ο: the set of truth-values {T, F}

ι: the set of individuals (the universe of discourse)

τ: the set of real numbers (doubling as times)

ω: the set of logically possible worlds (the logical space)

Hence, we can type both extensional and intensional entities. Extensions come in two flavours. Either an extension is a function that maps arguments of another type than ω to a type α (such as +, which maps pairs of numbers to a number), or it is a medadic function, i.e. a function without arguments, i.e. a function that coincides with its values, i.e. a constant. Individuals and truth-values are medadic functions. Intensions are polymorphous functions of type (βω), where β is frequently a chronology of α-objects of type (ατ); thus α-intensions are frequently of type ((ατ)ω), which will be abbreviated as ‘α_τω’. An object of type α_τω is a function from worlds to a function from times to α-typed objects. Some important extensional and intensional entities include:

• Characteristic function (here, set of individuals) / (οι)

• Set-in-intension (here, property of individuals) / (οι)_τω

• Individual-in-intension (individual office or role) / ι_τω

• Truth-value-in-intension (truth-condition or PWS proposition) / ο_τω

• Binary relation-in-intension (here, attitude) / (οια)_τω

The following schematic formula is characteristic of explicit intensionalization and temporalization: $\lambda w\lambda \mathrm{t}\left[\dots w\dots .t\dots \right]$with w_i ranging over ω and t_i ranging over τ. The schematic Closure denoted by this formula produces a function from possible worlds to a function from times to whatever the yet-to-be-filled-in sub-procedures and types specify.¹⁷ Reference to empirical indices such as worlds and times is not relegated to some meta-language. Instead, variables ranging over worlds and times are themselves (sub-)procedures and so contribute to how a particular type of entity is typed to be produced. Therefore, an ideography whose formulas represent procedures must refer to each sub-procedure occurring within a molecular procedure:

Definition 3

(sub-procedure).

Let C be a procedure. Then:

1. C is a sub-procedure of C.

2. If C is ⁰X or ²X and X is a procedure, then X is a sub-procedure of C.

3. If C is [X X₁ … X_n] then X, X₁, … , X_n are sub-procedures of C.

4. If C is [λx₁ … x_n Y] then Y is a sub-procedure of C.

5. If A is a sub-procedure of B and B is a sub-procedure of C then A is a sub-procedure of C.

6. A procedure is a sub-procedure of C only if it so follows from (i) – (v). □

4.3. Higher-order entities

The Closure above can itself be displayed by Trivialising it: ${}^0\left[\lambda w\lambda \mathrm{t}\right[\dots w\dots .t\dots \left]\right]$The Trivialised Closure occurs in displayed mode, as does any sub-procedure occurring within it. The Trivialisation of this Closure occurs in executed mode. This Trivialisation can, in turn, itself occur in displayed mode, with infinite iteration a theoretical possibility: ${}^{00}\left[\mathrm{\lambda w\lambda t}\left[\dots w\dots .t\dots \right]\right]$However, as soon as procedures are displayed, we have ascended into the higher-order realm of TIL:

Definition 4

(ramified hierarchy of types).

T₁ (types of order 1). See Definition 2.

C_n (procedures of order n)

1. Let x be a variable ranging over a type of order n. Then x is a procedure of order n over B.

2. Let X be a member of a type of order n. Then ⁰X, ²X are procedures of order n over B.

3. Let X, X₁, … , X_m (m > 0) be procedures of order n over B. Then [X X₁ … X_m] is a procedure of order n over B.

4. Let x₁, … , x_m, X (m > 0) be procedures of order n over B. Then [λx₁ … x_m X] is a procedure of order n over B.

5. Nothing is a procedure of order n over B unless it so follows from C_n (i)–(iv).

T_n + 1 (types of order n + 1). Let *_n be the collection of all procedures of order n over B. Then:

1. *_n and every type of order n are types of order n + 1.

2. If m > 0 and α, β₁, … , β_m are types of order n + 1 over B, then (α β₁ … β_m) (see T₁ ii)) is a type of order n + 1 over B.

3. Nothing is a type of order n + 1 over B unless it so follows from T_n + 1 (i) and (ii). □

Notational conventions. ‘y → α’ means that variable y ranges over type α. If C is a procedure, then ‘C → α’ means that C is typed to produce an entity of type α. That an object a is of a type α is denoted ‘a/α’. Thus, for instance, ‘C/*_n → ι’ means that the procedure C is of order n (i.e. belongs to type *_n) and is typed to produce an individual. That a variable v-constructs means that the variable constructs its product relative to a valuation v. Throughout this paper we use variables w → ω and t → τ. If C → α_τω then the frequently used Composition [[C w] t] → α will be written as ‘C_wt’ for short.

Definition 5 (existential and universal quantifiers).

The existential quantifier ∃^α/(ο(οα)) is a total polymorphic function that takes a set of α-typed elements to the truth-value T if the set is non-empty and otherwise to F. The general quantifier ∀^α/(ο(οα)) is a total polymorphic function that takes a set S of α-typed elements to the truth-value T if S contains all the elements of type α and otherwise to F. □

‘∃’, ‘∀’ are categorematic terms in TIL, namely functors that denote functions of the above type. Once a set produced by, e.g. λy [… y …] is inputted as an argument to ∃ or ∀, the quantifier returns a truth-value as value. The strings ‘∃y’, ‘∀y’ count as ill-formed in TIL, because all binding is λ-binding or ⁰-binding (see below for the definition). The proper notation is ‘[⁰∃λy [… y …]]’, ‘[⁰∀λy [… y …]]’. Anyway, for the sake of simplicity, we may stick to ‘∃y [… y …]’, ‘∀y [… y …]’, when no confusion can arise.

4.4. Partiality

TIL being a logic of partial functions, it is apt for dealing with, e.g. presuppositions, truth-value gaps, and non-referring terms. Yet partiality brings about technical complications. Propositions (i.e. truth-conditions parameterised to worlds and times), properties and relations can take the truth-value T at some worlds and times, F at others, and at yet other worlds and times have truth-value gaps. Two things. First, generating a formula of the form α∧¬α, though necessary, is not sufficient for a contradiction, in case it is required that the result is False, i.e. both conjuncts must be defined.¹⁸ However, we can relax this condition sufficiently, if we only demand that α∧¬α must nowhere and never be true. This leaves it open that a conjunct, or both, may be false or else undefined. Second, if not all the premises of an argument are true, some may be false and others gappy.¹⁹ Consequently, while entailment in a logic of partial functions is (obviously) truth-preserving from premises to conclusion, it is not falsity-preserving from conclusion to premises. To manage partiality properly, we need the empirical propositional property of True. For completeness, we also define two other propositional properties, namely False and Gappy, all of type (oo_τω)_τω. They are defined as follows (A → o_τω):

[⁰True_wt A] v-produces T if A_wt, otherwise F.

[⁰False_wt A] v-produces T if ¬A_wt, otherwise F.

[⁰Gappy_wt A] = ¬[⁰True_wt A] ∧ ¬[⁰False_wt A]

Hence:

Definition 6 (Analytical entailment).

Let P, Q₁, … , Q_n → o_τω be hyperpropositions. Then P is entailed by Q₁, … , Q_n, denoted Q_1, … , Q_n ⊨ P, iff ⁰∀λw [⁰∀λt [[[⁰True_wt Q₁] ∧ … ∧ [⁰True_wt Q_n]] ⊃ [⁰True_wt P]]]. □

4.5. Requisites

Given two intensions, one can, by definition, be made to supervene on the other. This family of supervenience relations-in-extension is called the requisite relations: one intension is said to be a requisite of another. Different types of intensions can be requisites of intensions of the same or different types. A typical example is the requisite relation between two ι-properties, as when the property of being a mammal is a requisite of the property of being a whale. Here is the definition, where ‘[⁰Req D C]’ means that the property produced by D is a requisite of the property produced by C, which translates logically into the latter property entailing the former property.

Definition 7

(Requisite relation between properties of individuals).

Let C, D be procedures such that C, D/*_n → (οι)_τω; x → ι. Then: [⁰Req D C] = [⁰∀λw [⁰∀λt [⁰∀λx [[⁰True_wt λwλt [C_wt x]] ⊃ [⁰True_wt λwλt [D_wt x]]]]]. □

The underlying idea behind requisites is that a set of requisites are individually necessary and jointly sufficient for an individual to instantiate the initial property.

The notion of requisite is our counterpart to the Meinongian’s Sosein, but there is an important difference. The Meinongian’s Vulcan is an inexistent object whose Sosein includes the property of being a planet. It counts as a truth that this inexistent planet is a planet. This predication has no direct Fregean counterpart. Vulcan is an office, and to predicate the property of being a planet of this office is to make a category, or type-theoretic, mistake. The right thing to say is that this property is among the requisites of this office. The correct bearer of this property is whatever individual happens to occupy the office at a given world/time pair. Likewise, from the truth of the reading de dicto of ‘Vulcan is an intermercurial planet’ it does not follow that there are intermercurial planets. What does follow is just that this property has been assigned to an office as a requisite.

We will walk you through an example. Priest (2005, 95, fn. 16) has us consider ‘the mermaid in my room’ and ‘the centaur in my room’:

If we had extensionality, it would follow that it is true that the mermaid in my room is the same as the centaur in my room. But this seems wrong. […] [A]rguably the mermaid in my room is identical with the creature in my room with the top half of a woman and the bottom half of a fish. If this is the case, then ϕ can be constrained appropriately. Thus, the following condition ensures that co-entailing conditions pick out the same object: if, for all s, @∣⊦_s⁺Ux(A(x) ↔ B(x)) then ϕϵxA(x) = ϕϵxB(x).

This is how we parse this formula: ‘If, for all evaluations of variables, it is true at the actual world that it holds for all x that x is an A only if x is a B then the (randomly selected) A-thing being a ϕ is identical to the (randomly selected) B-thing being a ϕ’. TIL agrees that the mermaid in Priest’s room is distinct from the centaur in Priest’s room, also when there is neither a mermaid nor a centaur in his room, i.e. the mermaid and the centaur in Priest’s room turning out extensionally indistinguishable. TIL also agrees that a mermaid is identical to a creature with the top half of a woman and the bottom half of a fish. It is easy to capture this by means of requisites:²⁰

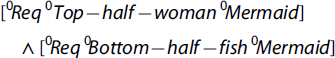
It may be instructive to consider how TIL fleshes out Priest’s example, as the way TIL handles it carries over to how TIL handles impossibilities. First, we define two different ι-offices (a Meinongian would speak of characterisation principles), where M′, C′, P are the properties being a mermaid, being a centaur, being in Priest’s room; M, C are the offices the mermaid in Priest’s room, the centaur in Priest’s room;  = /(οι_τωι_τω);  = ′/(οιι); ℩/(ι(οι)).²¹

Next, we express that these two offices are contingently co-occupied:

This Closure constructs the set of world/time pairs at which these two offices happen to be co-occupied. For [⁰= ′ [⁰M_wt ⁰C_wt]] to produce a truth-value, an individual would have to be the extension of both intensions. For [⁰= ′ [⁰M_wt ⁰C_wt]] to produce F, both offices would have to be occupied, though necessarily not by the same individual. This truth-condition goes unsatisfied in the actual world at the present time (or in 2005, for that matter). Both offices happen to be vacant, as per the assumption in Priest’s example. We say that ⁰M_, ⁰C are empirically empty procedures:

Definition 8

(Empirically empty procedure).

Let C be a procedure producing an intension. Then C is an empirically empty procedure at 〈w, t〉 iff the intension produced by C either (i) lacks a value at 〈w, t〉 or (ii) its value at 〈w, t〉 is an empty set. □

Remark. This definition is compatible with either necessary or contingent emptiness, leaving it open whether a given C is empty at all 〈w, t〉 or only some. Def. 9 below leaves room only for necessary emptiness.

Contingent co-extensionality is, obviously, far from enough to yield identity. Only co-intensionality entails identity of offices:

Type:  = /(οι_τωι_τω).

But, of course, M, C are two distinct offices, so the antecedent is false. We agree with Priest’s non-extensionalist stance that it is not true ‘that the mermaid in my room is the same as the centaur in my room’.

4.6. Dual predication

The availability of requisite properties enables predication de dicto, in addition to predication de re. TIL embraces dual predication, as in Zalta’s Object Theory, and unlike Priest’s MM. Informally, predication de dicto amounts to predicating a property of a dictum, which is either an intension or a hyperintension (procedure), while predication de re amounts to predicating a property of the extension of an intension or of the entity produced by a procedure. An argument in favour of dual predication might be a perceived structural or lexical ambiguity in a predication like ‘The Queen of Bhutan is a queen’. TIL excludes lexical ambiguity and stakes its case on structural ambiguity:

• Predication de dicto: being a queen is a necessary condition for being the Queen of Bhutan.

• Predication de re: the individual who happens to be the Queen of Bhutan is a queen.

These two different modes of predication will be captured by two different logical structures in the ideography. The definite description ‘the Queen of Bhutan’ is not lexically ambiguous in TIL, because it denotes the same entity in all contexts: the office of Queen of Bhutan.²² The feasibility of dual predication requires the technical ability to descend from the type of the office, ι_τω, to the type of the occupant, ι.²³ This is achieved by dint of functional application to worlds and times.

Qua office, this semantic value can occur either de dicto or de re, and the logical structure makes explicit which one it is. This suffices for present purposes:

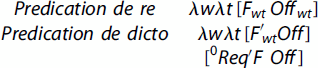
Types: F/*_n → (οι)_τω; F′/*_n → (οι_τω)_τω;; Off/*_n → ι_τω; Req^′/(ο (οι)_τω ι_τω).

λwλt [F^′_wt Off] is the logical form of a predication of a property of an office (not of its occupant), e.g. that the office happens to be vacant. As for λwλt [F_wt Off_wt] versus [⁰Req^′ F Off], ‘Vulcan has a molten core’ can be construed as predication de re or predication de dicto. Predication de dicto is tantamount to making having a molten core a requisite property of the Vulcan office. Predication de re is tantamount to predicating this property of the occupant of the office at the world/time of evaluation. It is important to understand that TIL describes predication in terms of what type of entity a given property is typed to be predicated of. The either contingent or necessary inexistence of a particular type of object does not affect the logic of predication either de re or de dicto. It will affect the truth-value, though. The type theory and the logical form together disambiguate which type of predication is the case.

Here are the three relevant schematic inferences pertaining to empirical, or ‘possible’, predication de re in the respective conclusions:

(1)	¬[0Occwt 0Off] ∴ [0Gappywt λwλt [0Fwt 0Offwt]]

Remark. It is irrelevant for the conclusion that F is a requisite of Off, so [⁰Req ⁰F ⁰Off] is not a premise. Similarly for ¬[⁰Req ⁰F ⁰Off].

(2)	[0Req 0F 0Off] [0Occwt 0Off] ∴ [0Fwt 0Offwt]
(3)	¬[0Req 0F 0Off] ∴ [0∃λw′ [0∃λt′ [0Fw′t′ 0Off w′t′]] ∧ 0∃λw′′ [0∃λt′′ ¬[0Fw′′t′′ 0Off w′′t′′]]]

where w′ ≠ w′′, t′ ≠ t′′. The open question is whether the world/time pair in the premises is identical to 〈w′, t′〉 or 〈w′′, t′′>.

Remarks. It is irrelevant for the conclusion that the office is occupied, so [⁰Occ_wt ⁰Off] is not a premise in (3). The validity of the derivation presupposes that Off is not impossible (not necessarily vacant).

We have generated a trifurcation of cases: gappiness, necessary truth, contingent truth or falsehood. For instance, having a molten core may not have been assigned to the Vulcan office as one of its requisite properties, nor follow from any requisite property assigned. To obtain a necessary falsehood, we need to negate an analytic truth, as in ‘It is not the case that Vulcan is [de dicto] a planet’ when being a planet is a requisite property of the Vulcan office. We obtain, e.g. ‘The intermercurial planet is not a planet’.

5. Applications

We turn now to a series of applications, adding further definitions as needed.

5.1. Non-intension-involving alethic impossibility

Non-intensions involving alethic impossibility are mathematical sentences like ‘Some squares are round’, ‘e is a natural number’, ‘The largest prime is even’ or ‘The largest prime is a prime.’ We are going to analyze the first and the fourth one.

5.1.1. Some squares are round

Already Meinong’s own variant of Meinongianism tackles the problem of impossible objects by introducing a distinction between being (‘there is’) and existence.²⁴ In cases involving predication, non-existent objects and existential generalisation, one obtains two variants:

• If a is an F, then there is something that is a.

• If a is an F, then a exists.

Within a Meinongian framework, these two readings are not equivalent. Since a Meinongian accepts only the weaker version (i) of the predication principle, the unacceptable inference (ii) is blocked. Applying these principles to impossible objects, the Meinongian obtains plausible results. The sentence.

‘Round squares are round and square’

expresses an analytic truth. Inferences like the following are also valid: ${\displaystyle \frac{\mathrm{The}\mathrm{round}\mathrm{square}\mathrm{is}\mathrm{round}\mathrm{and}\mathrm{square}}{\mathrm{There}\mathrm{is}\mathrm{something}\mathrm{that}\mathrm{is}\mathrm{a}\mathrm{round}\mathrm{square}}}$ ${\displaystyle \frac{\mathrm{The}\mathrm{round}\mathrm{square}\mathrm{is}\mathrm{round}\mathrm{and}\mathrm{square}}{\mathrm{There}\mathrm{is}\mathrm{something}\mathrm{that}\mathrm{is}\mathrm{round}\mathrm{and}\mathrm{square}}}$If ‘there is’ is synonymous with ‘exists’, these inferences come out invalid. However, on a Meinongian approach, these are acceptable consequences, since they do not entail the existence of something that is both round and square.

This solution seems to be plausible, and close to our hyperintensional approach. We are going to develop our counterpart of this distinction. While ‘there is’ concerns abstract objects like procedures or functions, ‘exists’ denotes a property of such abstract entities; namely, the property of producing an output entity (in the case of procedures) or the property of having a value at an argument (in the case of functions).

Accordingly, the sentence ‘There is a round square’ talks about a procedure, structured and typed to produce such geometric figures as are round squares, that is improper. On the other hand, the sentence ‘Round squares exist’ is understood to mean that some procedure structured and typed to produce round squares is successful in doing so. While the former expresses a truth, the latter expresses a necessary falsehood. Thus, in Meinongianism as in TIL, it is not only sensical, but also true, to say that there are non-existent and impossible entities and that non-existent, impossible entities do not exist.

Below we will be using the notion of a concept. A concept is defined, in TIL, as a closed procedure in normal form.²⁵ Intuitively, a concept is a procedure devoid of free occurrences of variables and with the most reduced structure possible. The basic idea behind our counterpart is this. There is a concept that is structured and typed to produce a non-empty set of geometrical figures that are round and square. However, this concept produces an empty set of such figures, as being round and being square are incompatible properties. That is, round squares do not exist. Formally, we obtain these analyses.²⁶

1. There is something that is round and square

2. [⁰Ǝλc [c = ⁰[λx [[⁰Square x] ∧ [⁰Round x]]]]]

Types: ∃/(ο(ο*₁); c/*₂ → *₁; x/*₁ → ι; Square, Round/(οι).

The above Composition produces the truth-value T. The set of procedures (λc) such that c is equal to the Closure [λx [[⁰Square x] ∧ [⁰Round x]]] is non-empty. Note that this Closure here occurs displayed, i.e. hyperintensionally. We are not talking about its product; rather, this very procedure is the object of predication.

1. Round squares exist

2. [⁰∃’ λx [[⁰Square x] ∧ [⁰Round x]]]

Type: ∃’/(ο(οι)).

This Composition produces the truth-value F. The set of individuals (λx) that are square and round is empty. Note that now the procedure [λx [[⁰Square x] ∧ [⁰Round x]]] occurs executed; we are talking about the product of the procedure.

5.1.2. The largest prime is a prime

For this kind of example, we need the following definition:

Definition 9

(Strictly empty procedure). Let C be a procedure. Then C is a strictly empty procedure iff C is improper. □

Remark. Since being improper is a property of procedures, it is of type (ο*_n). A procedure is improper simpliciter when it is v-improper for any valuation v.

There are persuasive reasons for any of these three interpretations of ‘The largest prime is a prime’:

1. true, because being a prime goes into the definition of the largest prime;

2. false, because whatever set of numbers is picked, none is going to contain the largest prime as a member;

3. gappy, because the largest prime is not around to make predication about this number either true or false.

Option (i) presupposes predication de dicto and hyperintensional occurrence of the concept of the largest prime. The sentence is understood like this: The concept of prime is subsumed under the concept of the largest prime. Option (ii) presupposes predication de dicto, paired with intensional occurrence of the concept of the largest prime. The topic of the sentence is ‘prime’, and it can be read as ‘Among the prime numbers there is the largest prime.’ Option (iii) presupposes predication de re, which comes with extensional occurrence of the concept of the largest prime.

The basic types we need are just two in number:

• ο

• ν (natural numbers)

To get started, we first lay down the structure of the meaning of the definite description ‘the largest prime’, ℩/(ν(ον)):

This Composition is typed to produce a set of primes and then extract its single element. However, as a matter of arithmetic fact, there is no such singleton. Hence, the Closure λy [[⁰Prime y] ∧ ⁰∀λz [[⁰Prime z] ⊃ [⁰≥ y z]]] produces the empty set of ν-typed entities. Hence, the function denoted by the functor ‘℩’ is undefined at the argument produced by this Closure. The logical effect is that the Composition is improper simpliciter.

The general pattern is to produce an empty set and then apply the ‘singularizer’ function ℩, which fails to receive a singleton as input and, therefore, fails to yield an output. This pattern applies to ‘the largest positive real number’, ‘the final decimal in the expansion of π’, etc., which also fail to denote. All three definite descriptions are co-extensional in the extreme sense that they are without extension. Of course, adherence to extensional individuation would spell disaster, as they would come out notational variants of one another. So where does fine-grained individuation come from? Two factors help avert disaster, namely type distinctions and distinctions in structure or constituents. Each type has its own empty set. Sets are characteristic functions, and so also empty sets are of the polymorphous type (οα). Therefore, the empty set of natural numbers is of type (ον) whereas the empty set of real numbers is of type (οτ). Hence, ℩ above is of type (ν(ον)) whereas ℩′ is of type (τ(οτ)). Therefore, the fact that one singularizer fails to be defined is distinct from the fact that some other singularizer also fails to be defined.²⁷ This still only makes for a rough individuation, because there is still just one empty set per type, but it is a step in the right direction. For instance, it already contributes to distinguishing structurally non-isomorphic procedures. The meaning of ‘the largest positive real number’ has this familiar structure, with x, y, z ranging over reals:

The other two differences from [⁰℩λy [[⁰Prime y] ∧ ⁰∀λz [[⁰Prime z] ⊃ [⁰≥ y z]]]] are ⁰Prime versus ⁰Positive as sub-procedures, and the fact that ⁰Prime produces an entity of type (ον) whereas ⁰Positive produces an entity of type (οτ). In virtue of these differences, the two Compositions [⁰℩λy [[⁰Prime y] ∧ ⁰∀λz [[⁰Prime z] ⊃ [⁰≥ y z]]]] and [⁰℩′λy [[⁰Positive y] ∧ ⁰∀λz [[⁰Positive z] ⊃ [⁰≥ y z]]]] are two distinct procedures. They are, strictly speaking, also structurally distinct procedures, because ⁰Prime and ⁰Positive, though both Trivializations of a property of numbers, are two distinct Trivializations.

Therefore, they are suitable as the respective meaning of two semantically different definite descriptions. The logical relationship between these two procedures is that they are both v-improper for all valuations v, hence v-congruent for all v, hence equivalent. As procedures bereft of a product, they are both roads to nowhere, but these are two different roads. Below we will go through each of the three options in more detail.

Option (i). The hyperintensional reading is ‘The concept of the largest prime subsumes the concept of a prime’, and it expresses a truth. Let C, D/*_n → (οα) be concepts of α-sets, i.e. closed procedures in their normal form typed to produce α-sets; x → α. Then:

Type: Subsumed/(ο*_n*_n): the relation of subsuming between concepts; True*/(ο*_n): the property of a procedure that it v-produces T for every valuation v.

For instance, the concept of a bachelor is subsumed under the concept of a man:

The concept of the largest prime is subsumed under the concept of a prime:

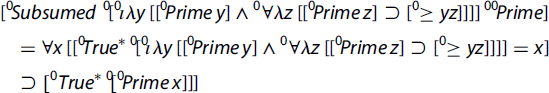
Option (ii) centres around intensional predication de dicto. This is a Russellian solution, and the sentence can be read, ‘There is a unique largest prime number, and this number is a prime’. On this reading the sentence expresses a falsehood, as we are going to show now.

Types: ∃/(ο(ον)); x, y, z → ν.

Since the first conjunct is gappy, the set of natural numbers produced by λx [… .] is empty, and the existential quantifier returns F. Note that the occurrence of the meaning of ‘the largest prime’ is now intensional due to the (λx)-generic context. We are predicating existence (non-emptiness) of a set of numbers rather than of a (non-existing) number.

Option (iii) centres around predication de re. This is the Strawsonian view of the definite description ‘the largest prime’.²⁸ The sentence not only entails but also presupposes the existence of the largest prime, which means that both this sentence and its negated form, ‘The largest prime is not a prime’, entail the existence of the largest prime. If there is no such number, the sentence comes out gappy. The structure of the de re reading of ‘The largest prime is a prime’ is this:

Any attempt at predication would grind to a standstill, if predication required us to first identify a referent and then predicate the property of it. This appears to rule out predication de re (extensional occurrence) as meaningful, though in TIL it does not. Again, because we are not invoking impossibilia, the right approach is not, even as a façon de parler, to describe an impossible prime number. We are describing no numbers. We are describing a logical procedure that is structured and typed to yield a number (here, a ν-typed entity) that satisfies a uniqueness condition applicable to ν-typed entities. Since Compositions may be improper, the Composition above can be parsed as ‘Whatever prime is the largest, if any, is a prime’. The Composition.

being strictly empty (improper), yields the result that the function produced by ⁰Prime fails to receive an argument and, therefore, cannot yield a value, in this case an ο-typed entity, i.e. a truth-value. Therefore, the Composition [⁰Prime [⁰℩λy [[⁰Prime y] ∧ ⁰∀λz [[⁰Prime z] ⊃ [⁰≥ y z]]]]] is improper. In TIL it is neither true nor false that the largest prime is a prime, when the predication involved is extensional.

5.2. Non-intension-involving doxastic impossibility

Examples of this kind of doxastic impossibility would be, ‘Tilman believes that the largest prime is a prime’ or ‘Tallulah believes that A is not truth-functionally equivalent to A∨(A∧B).’ We are going to analyse the first one, as the second is trivial.

5.2.1. Tilman believes that the largest prime is a prime

The type of the relation-in-intension denoted by ‘believe’ cannot be a relation between an individual and a truth-value. First, there is no such truth-value forthcoming, because the complement clause is gappy on its de re reading, as demonstrated above. And even if it were not gappy (i.e. if it were understood as being true on its hyperintensional reading or false on its intensional reading), it makes no sense to believe a truth-value. However, one can believe a truth-value-producing procedure: one believes that the procedure produces T. Hence, the entity Believe/(οι*₁)_τω is a relation-in-intension between an individual and the procedure encoded by the complement clause ‘The largest prime is a prime’, which is the Composition.

For the sake of simplicity, we now present the analysis of the above sentence in accordance with option (iii), which is arguably the most natural one:

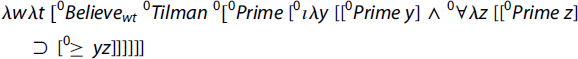
This Closure produces a proposition of type ο_τω that takes the value T or F at a given world w and time t of evaluation, according as Tilman is, or is not, in the relation of believing to the Composition [⁰Prime [⁰℩λy [[⁰Prime y] ∧ ⁰∀λz [[⁰Prime z] ⊃ [⁰≥ y z]]]]], even though this procedure is improper. This Composition is displayed by Trivialisation.²⁹

Having analyzed the sentence, we can derive consequences and prove the validity of arguments. For instance, we can apply the rules of natural deduction adjusted to TIL, such as existential generalisation. Quantifying over constituents of the assumptions (i.e. procedures occurring in the execution mode) is trivially valid: ${\displaystyle \frac{\mathrm{Tilman}\mathrm{believes}\mathrm{that}\mathrm{the}\mathrm{largest}\mathrm{prime}\mathrm{is}\mathrm{a}\mathrm{prime}}{\mathrm{Tilman}\mathrm{believes}\mathrm{something}}}$Formally, we have this argument (c/*₂ → *₁):

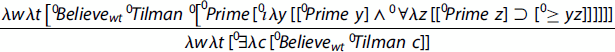
Trivially, there is a procedure c such that Tilman believes that c (namely, the procedure [⁰Prime [⁰℩λy [[⁰Prime y] ∧ ⁰∀λz [[⁰Prime z] ⊃ [⁰≥ y z]]]]]) produces T. It is important to note that the variable c belongs to the type of order 3, viz. *₂, because it ranges over the type of order 2, i.e. procedures of order 1, viz. *₁. The complement of the attitude (i.e. the Trivialised procedure ⁰[⁰Prime [⁰℩λy [[⁰Prime y] ∧ ⁰∀λz [[⁰Prime z] ⊃ [⁰≥ y z]]]]]) is a constituent of the premise; hence, we simply applied the ∃I-rule of natural deduction. This is a simple matter, because we just quantified over a believed hyperproposition, i.e. an entire hyperintensional context.

However, to quantify into a hyperintensional context amounts to considering the structure of a given procedure occurring displayed, and this is far from being straightforward.³⁰ One must be careful not to infer non-existing entities into existence. Attempting to do just that generates an inference like this one:

Hence, the validity of existential generalisation depends on the type of the entity being quantified away. One can quantify over procedures displayed within the hyperintensional context, like in this argument:

Trivially, there is such a procedure, namely [⁰℩λy [[⁰Prime y] ∧ ⁰∀λz [[⁰Prime z] ⊃ [⁰≥ y z]]]]. To obtain the product of the procedure v-produced by c/*₂ → *₁, we must apply the procedure of Double Execution (see Def. 1 iii). General, if procedure C produces procedure D and D produces entity E (either a procedure or a function), then ²C produces E. Specifically, if c produces [⁰℩λy [[⁰Prime y] ∧ ⁰∀λz [[⁰Prime z] ⊃ [⁰≥ y z]]]]/*₁, then ²c/*₃ → ν is typed to produce a number. However, careless quantifying is not truth-preserving, because in the hyperintensional context of a displayed procedure all the variables are bound by Trivialisation, which makes them unamenable to manipulation by logical operations.³¹ Hence, an argument such as this is invalid:

5.3. Intension-involving alethic impossibility

Examples of alethic impossibilities include ‘Ebenezer is a divorced bachelor’ and ‘Some Russell barber wears a wig’.

5.3.1. Ebenezer is a divorced bachelor

We stipulate that ‘Ebenezer is a divorced bachelor’ is equivalent (though not synonymous) to ‘Ebenezer is divorced, and Ebenezer is a bachelor’:

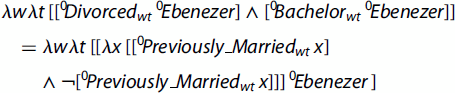
Either Closure produces a proposition of type ο_τω that necessarily returns F.

A logical step is required to obtain the explicit contradiction in the second Closure from the implicit contradiction in the first Closure. This step is known as refinement. A procedure can be refined into another procedure. In this case we are refining ⁰Divorced into [⁰Previously ⁰Married], Previously/(οι_τω οι_τω), and ⁰Bachelor into λwλt [λx ¬[[⁰Previously ⁰Married]_wt x]]. The definition of refinement presupposes the definition of ontological definition. Ontological definition contrasts with verbal definition, the latter being the introduction of a new term into a vocabulary rather than the introduction of a new entity into an ontology.³²

Definition 10 (Ontological definition).

Let C be a molecular closed procedure producing entity Y. Then C is an ontological definition of Y. □

Definition 11 (Refinement of construction).

Let C₁, C₂, C₃ be procedures. Let ⁰Y be a Trivialisation of Y, and let ⁰Y occur as a subprocedure in executed mode within C₁. If C₂ differs from C₁ only by containing instead of ⁰Y an ontological definition of Y, then C₂ is a refinement of C₁. If C₃ is a refinement of C₂ and C₂ a refinement of C₁ then C₃ is a refinement of C₁. □

Example. The Trivialisation ⁰Prime can be refined into the Closure λx [⁰Card λy [⁰Divide y x] = ⁰2].

Corollary. If C₂ is a refinement of C₁ then C₁ ≈ C₂, i.e. C₁, C₂ are equivalent procedures, but they are not co-hyperintensional. Co-hyperintensionality, in TIL, is known as procedural isomorphism.³³ Procedural isomorphism does allow minor procedural (hence structural) differences between equivalent procedures, but mere equivalence is too coarse-grained to qualify for procedural isomorphism. Any two procedurally isomorphic procedures are validly substitutable within a hyperintensional context. Also, we want to claim, without argument, that procedures producing ‘impossibilities’ are individuated up to procedural isomorphism. The open question remains, though, exactly which calibration of procedural isomorphism is right for such procedures.

5.4. Intension-involving doxastic impossibility

Examples of intension-involving doxastic or notional impossibility include ‘Tallulah believes that groundhogs are not whistle-pigs’, ‘Federico believes that whatever does not kill him makes him stronger, but not that whatever does not make him stronger kills him’, ‘Ebenezer believes that some orchids are reptiles’.

Our theory of intension-involving impossibilities is centred around Def. 12 and its corollary:

Definition 12 (Empirical procedure) Let C be a procedure. Then C is an empirical procedure iff C produces a non-constant intension. □

Corollary. A Closure of the form λwλt [… w … . t …] that produces a constant intension is a non-empirical procedure. This is as it should be, because there will be no divergence between any two random world/time pairs. There will be no point in selecting a world/time pair and checking the extension of the intension so produced, for we know already what the extension is going to be, if the intension is impossible: a gap or an empty set or F.

5.4.1. Ebenezer believes that some orchids are reptiles

This is the hyperproposition that is the complement of Ebenezer’s attitude:

This Closure produces the set of world/time pairs at which the respective local extensions of the properties being an orchid and being a reptile share a nonempty intersection. Only spelling out some of the requisites of either property will bring out the incompatibility of these two initial properties.³⁴ By invoking requisites, this example presupposes that it is not a nomological, but an analytic impossibility that some orchids should be reptiles.

Ebenezer’s cognitive predicament is that, although he understands these two properties well enough to form a belief involving both of them, he fails to calculate their incompatibility. If his attitude were a relation to a truth-condition, it would be a relation to the empty set of individuals in each world/time pair. In order to respect the nature of Ebenezer’s predicament, his attitude must be a relation to a hyperproposition whose product is the impossible proposition. Ebenezer is intentionally related to a procedure, but emphatically not also to its product. This, in a nutshell, explains both why computationally subpar agents (that is all of humanity right there) are capable of having incoherent beliefs at all and also why incoherent beliefs are fine-grained.

This is the analysis of ‘Ebenezer believes that some orchids are reptiles’, where the type of Bel is (οι*_n)_τω, a relation-in-intension between an individual and a hyperproposition:

This Closure produces the set of world/time pairs at which Ebenezer believes that the above Closure produces a truth-condition that is satisfied at the world/time pair at which he is having the belief that some orchids are reptiles.

Ebenezer will be stuck with this incoherent belief, unless and until he starts to make explicit enough of the requisites to realise their incompatibility. He cannot do so, however, without replacing his initial attitude complement with a different hyperproposition. And any such hyperproposition is not going to be procedurally isomorphic to the hyperproposition that was his original attitude complement.³⁵

5.4.2. Ebenezer is seeking Russell’s barber

Take Russell’s barber to be the office of the barber who shaves all and only those who do not shave themselves. Since Russell’s barber does not exist, we are dealing with an impossible concept; here, a procedure producing the necessarily empty ι-office. The attitude must be analyzed hyperintensionally, because there is just one necessarily empty ι-office, which can be produced by infinitely many procedures (impossible concepts).

The ontological definition of the office Russell’s barber is this procedure:

Types: x, y → ι; Shave/(οιι)_τω.

Thus, we have:

Types: Seek/(οι*_n)_τω; Ebenezer/ι.

Though Ebenezer’s pursuit is doomed to fail, we can quantify over the hyperintensional context to infer that Ebenezer is seeking something: ${\displaystyle \frac{\mathrm{Ebenezer}\mathrm{is}\mathrm{seeking}\mathrm{Russel}{\mathrm{l}}^{\mathrm{\prime }}\mathrm{s}\mathrm{barber}}{\mathrm{Ebenezer}\mathrm{is}\mathrm{seeking}\mathrm{something}}}$

Type: c/*₂ → *₁.

6. Conclusion

We have outlined a structuralist counterproposal to the model-theoretic and world-based circumstantialist theory of impossibility. Our theory was developed within the inherently hyperintensional framework of Transparent Intensional Logic. Hyperintensions are identified with abstract logical procedures, which are structured and typed to produce products of a specific logical type. The framework proceeds in a strictly top-down fashion, with hyperintensions at the top, intensions in the middle, and extensions at the bottom.

Impossibilities constitute a cluster of limiting cases within TIL. Some procedures fail to produce a product. This is so in the case of non-empirical impossibility, where we bypass the intensional level and fail to identify an object at the extensional level. This is as it should be, because our ontology does not include, say, a rational e or a trilateral pentagon. Still, we can describe a procedure structured and typed to produce entities with these properties. Other procedures produce an impossible intension. This is an intension, of a specific type, whose condition goes unsatisfied in all worlds at all times. Such intensions include, for instance, the proposition that is nowhere and never true, the individual office that is invariably vacant, or the property whose extension is always the empty set of individuals. There are infinitely many procedures producing each of these intensions.

The overall picture that emerges is that impossible objects are not objects that are impossible, but no objects at all. Instead, impossible objects are procedures that are structured and typed to produce entities whose defining properties form an incoherent combination and so cannot possibly be instantiated. Ours is a theory of various impossibilities that invokes no impossibilia.

Acknowledgements

This research has been partly supported by a Grant from SGS No. SP2024/108, VŠB-Technical University of Ostrava, Czech Republic, “Application of Formal Methods in Knowledge Modelling and Software Engineering VII”, and also by the University of Oxford project “New Horizons for Science and Religion in Central and Eastern Europe” funded by the John Templeton Foundation (subgrant ‘The Necessity of God's Existence: Divine Names and Modality’). The opinions expressed in the publication are those of the author and do not necessarily reflect the view of the John Templeton Foundation. Earlier versions of the paper were presented by Bjørn Jespersen at the conference LACompLing2021, Mathematical Linguistics (MALIN) 2021, Université de Montpellier (UM), 13-17 December 2021 (online); at the workshop Beyond Impossible: Logical and Philosophical Perspectives, Padova, 22 October 2021; at UConn Logic Group, 30 April 2021 (online); and at the Tilburg Issues of the (Im)possible Conference, 17-18 October 2022.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Notes

1 See Ripley (2012) for the distinction between structuralist and circumstantialist strategies for obtaining fine-grained content. A different sort of structuralism might be truth-maker theories, where a proposition is identified with its mereologically structured collection of truth-makers. Truth-maker theories come with a heavy bottom of truth-makers, and for this reason do not qualify as structuralist in the narrow sense of this paper.

2 Sylvan’s box, marked ‘impossible object’, is both empty and contains a figurine (Priest 1997). Had this been so in the actual world rather than a short-story, the actual world would have been inconsistent, though in an un-‘explosive’ manner. Impossible worlds, technically speaking, will then not be needed to capture any of these inconsistencies. But the consistency constraint standardly applying to the propositions generated by possible-world semantics must be relaxed accordingly. We must not generate the unwarranted paradox that an impossible world is possible.

3 Also, truth-values are assigned to formulas/propositions at impossible worlds at will, which dismantles compositionality in IW. See also MacPherson (1993, 16–17).

4 Jago (2015, 714) says, ‘Hyperintensionality worries aside, the world-based approach is the most comprehensive and systematic account of content on offer. […] As always in science, the rational approach is to begin with our best theory, and modify it so as to avoid phenomena which it does not currently accommodate.’ However, one could object that if the worlds-based approaches need impossible worlds in order to function properly, then being stuck with them as a necessary condition tells against the worlds-based approaches altogether. This is not a conclusion we draw, however. We want to keep possible worlds for the purposes of intensionality, while realizing that impossibility is inherently a hyperintensional problem and as such cannot be satisfactorily accounted for by a world-based approach.

5 Lewis pushes this circularity objection, arguing that only his modal realism as per concrete (rather than ersatz) worlds avoids circularity. See (1986, Ch. 3).

6 The notion of dual predication, which divides into predication de dicto and de re, will be explained and applied in sections 4 and 5. The Meinongian circumstantialist does not themselves call it predication de re, but simply predication, because dual predication is not a feature of Meinongian circumstantialism. It is, of course, very much a feature of Zalta’s Meinongianism, which belongs in the structuralist camp. See Bueno and Zalta (2017) and Priest et al. (2020) for a dispute within the neo-Meinongian camp.

7 See Tichý (1988, 181). Cf. also (2004, 728): ‘Meinong’s ontology is deficient, not in admitting too much, but in admitting too little [i.e., admitting pure objects, objects beyond being and non-being, while not admitting bare particulars as bearers of properties]. [By lumping a bare particular, which is something, together with what it is] Meinong cannot distinguish between an attribute’s being instantiated by a particular and the same attribute’s being a requirement of a thing-to-be [i.e., an individual-in-intension]. Instead of saying that Pegasus, the pure object, is such that whatever is to embody it must be a horse, Meinong has to say that the pure object itself is a horse. And this is what gives Meinong’s ontology its fairy-tale twist: Meinong is committed to contending that some horses have wings, some mountains are golden, and so on. […] By ascribing empirical properties directly to the pure objects themselves, Meinong, as it were, makes them all come alive in a bizarre world teeming with Santa Clauses, unicorns and 56-eared pink elephants.’

8 Soft necessity, which characterizes nomological necessity according to Dretske, Tooley, and Armstrong, is mirrored by soft impossibility, which can be captured by a logical space of logically possible worlds partitioned into equivalence classes, each with its own laws of nature (with room for overlap with other equivalence classes). The polar opposite is dispositionalism (see Bird 2005), which rules out nomological alternatives: at no world does salt fail to dissolve in water; etc.

9 The circumstantialist’s objectives may be less ambitious. They just want the right inferences to come out valid, and their impossibilia, including impossible worlds, are just formal artefacts of the theory that do not purport to model anything outside of the theory.

10 Hicks (2022) shares similar misgivings about impossible-world semantics. Hicks adds that his account addresses metaphysical counterpossibles and does not readily extend to mathematical or logical counterpossibles.

11 There is an instructive parallel in the theory of property modification. A fake banknote is not a banknote that is fake. It is not a banknote, and it is not fake simpliciter, but fake relative to the property of being a banknote. The problem then arises what exactly a non-intersective (hence, non-extensional) account of the property of being a fake banknote amounts to. The typical answer is that fake operates directly on the property being a banknote. This way the population of any extension of being a banknote becomes irrelevant; we remain at the level of intension-to-intension mappings. The friend of impossibilia, however, could stipulate that a fake banknote, when existing at an impossible world, is indeed a banknote at that world. But it is not obvious how to accommodate the relativity of fake. Should this turn out to be a problem, then an impossibilist intersective account, ‘A fake banknote is (unqualifiedly) fake and a banknote’, will need some work.

12 Cf. also Tichý (1988, 178), ‘Since determiners [:intensions] are not always mutually independent, not every combinatorically possible determination system is [logically] realizable. It is impossible, for example, for the determiners white and black to pick out overlapping classes of individuals. It is not possible for the proposition The author of Waverley is a poet to pick out T when [the determiner the author of Waverley] picks out nothing. Thus not every determination system is a possible world. But every possible world is a determination system.’

13 There is a (fine?) line between impossibility and various degrees of nonsense.

14 The procedure called Double Execution, which embodies the transitivity of product-producing, is an exception, though. Double Execution interweaves procedures and executions of procedures, because one procedure presupposes the execution of a prior procedure. However, nothing in this paper hinges on this special feature of Double Execution. See also section 5.2.1 below.

15 The condition is directed at empirical indices; an intension challenges a world (or world/time pair, or first a world then a time) to be such that it returns a non-empty set, the truth-value T, an individual, etc. For background, Simchen (2004) contrasts the ‘pre-revolutionary’ conception of modality found in Carnap, Church, etc., with the ‘revolutionary’ conception found in Kripke, Kaplan, etc. The difference is pivoted on whether concepts/intensions/conditions (i.e., the ‘top’) or objects/extensions/satisfiers (i.e., the ‘bottom’) are conceptually prior. The former conception, which we subscribe to, concocts concepts/etc. at will, leaving it to ‘the world [to supply] mere satisfiers for independently constituted conditions’ (ibid., 531). Of course, the actual world, or any world, may fail to supply satisfiers. An object-first theory such as causal reference theory, which is restricted to entities encountered in the unique possible world that is physically realized, cannot put the predicates ‘is a zebra’ and ‘is a unicorn’ on an equal semantic footing. A concept-first theory like TIL can, though, thanks to the inversion of the direction of fit. The role of the physical world is to determine which intensions have instances and which individuals instantiate them. For further discussion, see Duží, Jespersen, and Materna (2010, 368–69).

16 TIL does come with a modal logic, but it is just vintage S5 with a constant domain. Hence, the Barcan and Converse Barcan Formulae come out unproblematically valid, as they just rehearse a couple of logical trivialities. See Jespersen and Duží (2022, fn. 41, §3.6).

17 Modal and temporal variation are handled separately, unlike in λwt [… w … . t …], which produces a binary function. See Duží, Jespersen, and Materna (2010, §2.5). It is a stretch when in the main text we speak of ‘world/time pairs’. However, this is harmless here, because there is no need to keep one parameter fixed and the other floating.

18 Cf. Duží, Jespersen, and Materna (2010, 277).

19 It does not hold for all of our propositions/ο_τω that either A or else its negation, λwλt [­A_wt], is true. In model-theoretic terms, our propositions do not amount to an ultrafilter for want of negation completeness. They do amount to a filter, though, because the impossible proposition is excluded and we have closure under conjunction and implication.

20 The properties of being a creature with a top half of a woman and being a creature with the bottom half of a fish are produced by means of property modifiers. However, here we are skipping the steps of producing these two properties by means of modifiers and Compositions, and going straight to their respective results.

21 If typed in TIL, ϵ would be of type (ι(οι)), just like ℩. Relative to a world/time pair and then relative to a set of individuals (namely, the satisfaction class of a property), at most one individual is selected. The difference is that the set need not be a singleton. ϵ is defined, even when the input set has more than one member, whereas ℩ demands a singleton in order to be defined. There is no need for choice functions in TIL, because TIL does not need an individual of which to predicate properties. TIL needs the type of an individual for predication to work.

22 One obvious procedure for producing this office would be this Closure:

λwλt [⁰Queen_of_wt ⁰Bhutan], where Queen_of /(ιι)_τω; Bhutan/ι.

23 Otherwise, what we like to call ‘the argument from the wrong argument’ kicks in: the functional argument provided is of the wrong type, leading to the predication of the property of being a queen, applicable to individuals, to the office of Queen of Bhutan. This argument is standardly levelled against theories, such as TIL, that have terms denote intensions (e.g. offices) when rival theories would have them denote extensions (e.g. individuals).

24 See Meinong (1960).

25 See Duží, Jespersen, and Materna (2010, §2.2).

26 For the sake of simplicity, we assign the type ι to geometrical figures; this simplification is harmless here. For details on the analysis of existence, see Duží, Jespersen, and Materna (2010, §2.3).

27 In more imaginative language, ‘the largest prime’ expects a singleton of natural numbers to operate on, whereas ‘the largest positive real number’ expects a singleton of real numbers to operate on. These are two different expectations, neither of which is met. One failed expectation does not spill over into the other failed expectation.

28 For an analysis of Russellian vs Strawsonian reading of definite descriptions, see Duží (2014), (2009).

29 Note that if the attitude were knowledge rather than belief, the proposition produced by the Closure would necessarily be undefined, because knowledge is factive. For rules for dealing with factives, see Duží and Fait (2021, §1.4.1), and Duží, Jespersen, and Materna (2010, §5.1.6).

30 See Jespersen and Duží (2022) for formal details and philosophical exposition.

31 Since λ-binding is weaker than Trivialization-binding, c is displayed rather than executed and thus immune to valuation. The way out is applying the substitution method developed in TIL to unlock the variable from Trivialization-binding. See Jespersen and Duží (2022).

32 Ontological and verbal definitions are the TIL counterparts to real and nominal definitions. See Duží, Jespersen, and Materna (2010, §2.2.2.2) for details and discussion.

33 When very finely individuated, two procedures are procedurally isomorphic only if they share the same structure up to α-conversion. Depending on the discourse we analyze, some other λ-conversions can be involved, for instance, restricted β-conversion or η-conversion. Yet, there is no universal criterion for procedural isomorphism that would be indiscriminately valid for every type of fine-grained discourse. See Duží (2019).

34 Duží et al. (2023) develops a method that enables us to discover inconsistencies in specifications of individual-concepts and thus prove that such concepts could not possibly be matched by an extension. The method centers around hyperrequisites of an impossible concept, and calculate for a given hyperoffice whether it constructs the impossible ι-office, which is necessarily vacant because any procedure for producing it is logically inconsistent. The method can be easily generalized to impossible properties and other impossible intensions.

35 Suppose that agent a believes that some proper subset S’ of S is the same size as S. Is a’s belief incoherent? This is indeterminate, because a’s belief is underspecified. It needs to be specified whether S is a finite or an infinite set. If finite, then incoherent. If infinite, then coherent. In either case, a’s belief must be analyzed as hyperpropositional, as all mathematical attitudes, but if an incoherent one, then different things (do not) follow.