How numbers influence students when solving linear equations

ABSTRACT

Most students need to learn to solve equations as a part of their education, but far from all succeed. In this study we investigate the potential impact of variation in the choice of numbers as coefficients when students in upper secondary school solve linear equations. A test with linear equations was distributed to 111 16-year-old vocational students and phenomenographic interviews were performed with 23 of them. The findings show that exchanging coefficients (e.g., changing a and b in $\mathit{a}=\mathit{b}\cdot \mathit{x}$) from natural numbers to other numbers significantly changes how equations with the same structure are handled, despite access to a calculator. A framework of five conceptions is described explaining how numbers are experienced in the foreground or background of attention, partly depending on what meaning the equation is given. The results indicate that number types need to be considered, not only in teaching arithmetic, but also in algebra.

KEYWORDS:

• Equation solving
• algebra
• phenomenography
• coefficients

Introduction

Linear equations are a central part of algebra teaching in upper secondary schools. Algebra enables representing and transforming abstractions, and yields powerful mathematical tools, forming in many ways a gatekeeper to studies in other areas, such as for instance chemistry and physics. Although it being crucial in mathematics education, many studies show that students struggle to learn algebra and equation solving (Bush & Karp, 2013). Despite many important findings on what strategies are most rewarding for students to engage in (Andrews & Öhman, 2019; Vlassis, 2002), or how students interpret the equal sign and the variable with their previous experience (Asquith et al., 2007; Christou et al., 2022; Sumpter & Löwenhielm, 2022), it seems that the difficulties of the topic remain for students.

Many studies have registered students’ computational issues regarding numbers in algebra (Bush & Karp, 2013). Still, it is not as common to look at how the type of numbers affects students’ interpretations of algebraic content. For example, students’ experiences of negative numbers and fractions are often omitted in research on algebraic thinking (Kieran, 2022; Vlassis & Demonty, 2022). However, the role of different number domains has been suggested as a possible cause for difficulties in algebra (Stephens et al., 2017) and the role of knowledge of numbers for algebraic thinking has been proposed as an area in need of more research (Linchevski & Livneh, 1999; Pittalis et al., 2018). Therefore, this paper inquires whether the nature of numbers influences how students experience linear equations and their ability to identify algebraic structures and to solve equations in efficient ways. This investigation is made in upper-secondary school in Sweden, in vocational education focusing on the topic of electricity. The 16-year-old students have learnt to solve linear equations in earlier years and the competence is relevant for their vocational studies. The aim of this paper is to contribute to the existing knowledge on why some students fail to solve equations when coefficients are numbers with decimals or negative integers, when they have solved similar equations with natural numbers using formal methods (Holmlund, 2022; Vlassis, 2002).

Background

The significance of how we experience equations can be exemplified in a historical reflection concerning Francois Viète (1540–1603). He is famous for developing symbolic algebra in the 16^th century, which led to considerable progress in the mathematical field (Viète & Witmer, 2006, p. 5). His greatest contribution was, however, not writing the unknown quantities as symbols – as this was done before him – but symbolizing “the givens” in the equations as letters (Drijvers et al., 2011; Viète & Witmer, 2006). Viète saw the generalizing aspect of the equations primarily in the coefficients. By introducing a new notation for this, a different way of perceiving equations was made possible and contributed to new powerful ways to develop the mathematical field.

In the two following sections research on the influence of the nature of numbers on students’ equation solving is reviewed, first concerning the role of numbers in algebra and thereafter in relation to the equation solving process.

Numbers in algebra

The nature of the relation between arithmetic and algebra is a debated topic (Wettergren et al., 2021), but many researchers describe this connection as essential (Kaput, 2008; Kieran, 2018; Pittalis, 2022). When generalizing arithmetic to learn algebra, Kaput (2008) means that arithmetic expressions should be viewed in a new way – looking at their form rather than their value. However, to ignore a number’s value and think of “any number” can be challenging as numbers through schooling tend to become “loaded entities, entities that children are encouraged to take into consideration, to refer to – not to ignore” (Linchevski & Livneh, 1999, p. 192).

Several studies report knowledge of numbers and operations as prerequisite arithmetic skills that influence students’ algebraic proficiency (Bush & Karp, 2013). Some of these are specific to numbers of a particular form, for example, to think that 2.35 is less than 2.305 as fewer digits indicate a lower value when natural numbers are concerned (Resnick et al., 1989). Other (mis)conceptions that are carried over to the algebraic context involve both numbers and operations, such as the expectation that multiplication generates a larger number (Christou & Vosniadou, 2012; Christou et al., 2022) and the difficulty in connecting knowledge of operations to other number domains, which can be seen as students often expect the answer, or literal symbol in an equation, to represent a natural number (Christou & Vosniadou, 2012; Christou et al., 2022; Warren, 2003). However, there are not as many studies that relate students’ experiences of the nature of numbers to their ability to identify algebraic structures. Linchevski and Livneh (1999) describe how similar structures of an expression, but with different numbers, can lead to varying degrees of detachment of the minus sign by students. In their results they display the example of students erroneously believing that $50-10+10+10=50-3\cdot 10$, but to a lesser frequency erroneously believing that $167-20+10+30=167-60$. Even though this example is not due to the nature of the numbers, it shows how biasing number combinations can misguide students’ attention. Other examples of studies that have shown connections between the choice of numbers and difficulties in interpreting equations, report on the challenge of giving equations a concrete meaning due to fractions (Hackenberg & Lee, 2015) or negative coefficients (Gallardo, 2002; Vlassis, 2002, 2008), or a general difficulty to view negative numbers in equations as objects with their signs “attached” (Vlassis, 2008; Vlassis & Demonty, 2022). In this way, numbers are occasionally considered relevant for algebraic thinking not only as a prerequisite for calculations, but as a vital part in the interpretation of the equation.

Equation solving

Returning to the connection between generalizing and how we think of numbers, we can see that linear equations can be solved with the numbers in focus to a lesser or greater extent, for example, when comparing methods such as trial-and-error substitution, and the use of number facts, with the transposing of terms (Kieran, 1992; Xie & Cai, 2022). The frequent topic of how students perceive equality – with either a procedural or a relational view (Tossavainen et al., 2011; Tuominen et al., 2018; Wettergren et al., 2021), for example, seeing the solving of $37=7\cdot \mathit{x}+2$ either as arithmetically “undoing” what has been done to x, or as a relation between numbers that can be rearranged – also gives a qualitative difference to how the numbers are approached. Still, structure is seen when using both methods, although the structure is arithmetic in the first case and algebraic in the latter.

To review more closely what it means to see structure, the term structure is here used to denote an internal order (i.e., a specific relation) between quantities and operations – which can either be seen directly in the equation or when it is transformed (Hoch & Dreyfus, 2004). From this definition, we can conclude that an internal order (i.e., structure) in an equation can only be identified if a student has an interpretation of the equation that makes it possible to recognize a familiar arrangement. This interpretation of the structure, that students rely on while transforming equations, is here referred to as the meaning seen in the equation (Balacheff, 2001; Kirshner, 2001). This meaning can either be a pragmatic control of a solution, interpreting symbols with the referent world (Balacheff, 2001), or a theoretical control, suspending the meaning of symbols while manipulating them (Boero, 2001; Dettori et al., 2001). The two ways of seeing meaning can be described with two terms borrowed from linguistics: semantic and syntax. Either the focus is on the semantics of the symbols – considering what the mathematical objects represent – for example, seeing $7\cdot 5+2$ as representing seven groups of five red marbles and two blue ones, or the focus is on the syntactic nature of the mathematical objects presented – working with symbols using axioms, mathematical theorems, and rules (Carraher & Schliemann, 2007; Kirshner, 2001) – for example, seeing in $7\cdot 5+2$ that the rules of priority distinguishes an order in which to do the operations.

The different meanings, semantic or syntactic, are what students use for ordering the objects in an equation and discern structure, and with which they can further make generalizations. For the equation solver, the role of the coefficients is slightly different in these two activities of structuring and generalizing. The structuring activity calls for “seeing through mathematical objects” (Kieran, 2018, p. 101), for example, seeing the form of the numbers, whereas the generalizing activity calls for seeing the number as the underlying context for equations and a domain of applicability (Venkat et al., 2019). In this way, identifying structure and making generalizations display the algebraic activity as twofold; it concerns looking for relationships through the formatting and decomposing of expressions, and making generalizations of the found relationships (Kieran, 2018; Venkat et al., 2019). These two activities are intertwined, as an emergent structure is seen when a structure is discerned in local cases (e.g., $819=39\cdot \mathit{x}$ can be rearranged as $\frac{819}{39}=\mathit{x}$), while actions of generalization are required to see the same structure as a mathematical structure (Venkat et al., 2019), i.e., seeing that the identified property holds across some class of examples (e.g., also $0.657=0.45\cdot \mathit{x}$ can be rearranged as $\frac{0.657}{0.45}=\mathit{x}$).

It has been registered that a change of numbers in an equation can make students unable to recognize (Holmlund, 2022) or solve (Vlassis, 2002) an equation they otherwise are familiar with. However, there are – as we have seen – several reasons suggested of how numbers can influence: as (mis)conceptions, in the way they direct one’s attention, and in their degree of abstractness. Instead of focusing on one of these issues specifically – as some of the previously mentioned studies in this paper already has – this study adds to research by setting out to give a description of all the influence that the nature of numbers has on students as they solve equations. This can give a comprehensive overview of which of the aspects reviewed, concerning numbers and solving equations that are relevant for the ability to see structure in equations with different numbers.

First, to explore the relevance of number’s domain, quantitative methods have been used – distributing and analyzing a test on equations with the same structures but with coefficients from different domains (natural numbers, negative numbers or numbers between zero and one on decimal form, here referred to as numbers with decimals). Secondly, to learn more about how the numbers influence students’ experiences of the equations – interviews with a phenomenographic approach (Marton, 1981, 2014; Marton & Booth, 1997) were employed. The following questions have guided the research:

1. How is the ability to solve linear equations affected by the choice of coefficients in different domains (e.g., positive or negative integers, or numbers with decimals) for 16-year-old upper-secondary students?

2. In what ways do 16-year-old students experience the solving of linear equations when the coefficients are natural numbers, negative numbers, or numbers between zero and one on decimal form?

Methods

In order to both display the extent of numbers’ influence and the reasons behind, the data consist of a test (n = 111) and 23 student interviews. The phenomenographic research approach has guided the research process – mainly the analysis of the interviews in the second part – wherefore it is initially described here. Thereafter the process of data collection is described, and finally the analysis process.

The phenomenographic approach

That powerful ways of handling a phenomenon come from powerful ways of seeing that phenomenon, is a basic assumption within the phenomenographic research tradition (Marton, 2014; Marton & Booth, 1997). This research tradition shares the view of Gurwitsch (1964) that different aspects of a phenomenon can be in the foreground or background of our awareness, depending on what is noticed and in what context it is experienced. A way of experiencing a phenomenon at a particular point in time can be described by what aspects that are discerned and focused (Marton & Booth, 1997). As an experience of a phenomenon changes when other aspects are focused, different ways of experiencing can occur in the same interview. In contrast to other research approaches, knowledge is not considered as static – something that someone has or has not – but is rather seen as an internal relation between the learner and the object (Björklund et al., 2021). Consequently, students are not seen as having misunderstandings – but rather there are different ways of perceiving a phenomenon, where in some of these, certain aspects are not yet discerned and focused. This gives a direct indication to teaching what aspects that need to be visualized. The research interest is therefore directed toward the second order perspective, how an object can be experienced by the learner (Marton, 1981).

Each way of seeing the phenomenon includes, to different extents and with varying focus, grasping the same aspects of a phenomenon (Marton & Booth, 1997). The idea of a phenomenographic study is to find the different ways of experiencing a phenomenon within a group of people and describing the essential variation in what aspects that are discerned – so we learn what aspects that are critical for perceiving in a more refined way. Individual variation in a way of experiencing, such as taste or feelings, are then ignored. The ways of experiencing (which is used synonymously with ways of seeing and conceptions) are usually ordered hierarchically depending on whether relevant aspects are discerned, and are usually presented in an outcome space, a complex of distinct descriptions of ways of experiencing (Marton, 1981, 2014; Marton & Booth, 1997).

This research approach has guided several studies in mathematics education to the identification of students’ experiences of a phenomenon and the aspects of these that are critical for learning (Björklund et al., 2021; Neuman, 1999; Tossavainen et al., 2011; Tuominen et al., 2018; Wettergren et al., 2021). Given the phenomenographic approach for this study, the ambition for the qualitative data collection is to search for students’ different ways of experiencing equations with different numbers. The intent is to describe what makes these ways of experiencing distinct from each other and critical for learning. This process is described further in the analysis section.

Data collection

Initially, a test item with 10 equations was created (see Table 1). It included equations of three different structures: $\mathit{a}=\mathit{b}+\mathit{x}$, $\mathit{a}=\mathit{b}\cdot \mathit{x}$, and $\mathit{a}=\mathit{b}\cdot \mathit{x}+\mathit{c}$, where a, b and c are natural numbers, negative integers, or numbers with decimals (see Table 1). The specific equations were selected with the intent to display possible variations in students’ experiences of similar equations. In this way the test has a within-subject design (Shadish, 2002), where the student is exposed to different treatments, the different equations. For the multiplicative equation several versions were chosen as $0.12=0.4\cdot \mathit{x}$ and $-24=6\cdot \mathit{x}$ were found interesting from other studies (Holmlund, 2022; Vlassis, 2002). We also wanted to elaborate on the size of the natural numbers ($42=3\cdot \mathit{x}$ and $819=39\cdot \mathit{x}$), the amount of digits in the numbers with decimals ($0.12=0.4\cdot \mathit{x}$ and $0.657=0.045\cdot \mathit{x}$) and include the generalized form ($\mathit{a}=\mathit{b}\cdot \mathit{x}$). The equations were arranged in different order in two printed versions of the test – mixed – as not to encourage transfer of solution method. To confirm that the students did not obtain erroneous results due to difficulties in handling the calculator, each test included three initial questions for the students to type on the calculator. The quality of the test items was satisfactorily tested in a pilot study.

Table 1. Overview of the ten equations in the test.

Typeof coefficients	Additive structure	Multiplicative structure	Additive and multiplicative structure
Natural numbers	$352=63+\mathit{x}$	$42=3\cdot \mathit{x}$ $819=39\cdot \mathit{x}$	$37=7\cdot \mathit{x}+2$
Numbers with decimals	$2.01=0.434+\mathit{x}$	$0.12=0.4\cdot \mathit{x}$ $0.657=0.045\cdot \mathit{x}$*	$2.5=0.8\cdot \mathit{x}+2.1$
Negative numbers		$-24=6\cdot \mathit{x}$
Symbolic		$\mathit{a}=\mathit{b}\cdot \mathit{x}$

*The equation was added to the test after the first class had taken it.

The test was distributed to seven classes in two cities in Sweden in the autumn of 2020. The participating 111 students were studying their first year of vocational education in upper secondary school. During this year in school, students turn 16 years old. However, data concerning age was not collected. One student did not use the calculator on either the control questions or the equations and was therefore excluded from analysis. Linear equations are a mandatory subject matter in lower secondary school, wherefore all students have been taught the subject before. Now attending upper secondary school, the students had either not yet returned to the topic or were presently engaged in it. The tests were distributed to the students during ordinary classes by the researcher, and it was made clear that this was not part of their regular course. The goal was to give the students as much time as they needed to fill in all the answers of the test in a, to them, satisfactory way. The time-limit was 40–50 minutes (including instruction) depending on the scheduled time of their present lesson. Most students did not use all the offered time for the test. The test was anonymous, except for the students who signed their name to confirm their willingness to be interviewed.

To gain further insight on how students experience structures with varying types of numbers, the equations from the test were used in task-based interviews with a subset of 23 students (Björklund et al., 2022; Neuman, 1999). Informed written consents were given. Using a phenomenographic approach, the aim is to find all qualitatively different ways to experience a phenomenon within a group (Marton, 1981; Marton & Booth, 1997). Therefore, the objective when selecting students for interviews was to obtain the widest possible range of ways of experiencing the structure of the equations – choosing students with both low, medium and high scores from the test and with different ways of explaining their answers. This selection process was made continuously during the interview period, depending on the data that had been collected so far, to complement the range of ways of experiencing. During the last interviews, no new ways of experiencing the structure of equations occurred and after 23 completed interviews, the data-collection was terminated.

The interviews were conducted during students’ ordinary lessons, in a separate room. There, the students met a selection of equations from the test in a varying order. The equations were presented on a piece of paper, to probe students’ understanding of the structure of the equations and give them the same access to the phenomenon. The students had access to a calculator during their interview. The researcher asked questions such as “What do you think of this?” [referring to the displayed equation], “How do you know that?”, “How would you explain this to a younger student who does not know equation solving?” and similar questions aiming for clarification in their conceptions of the phenomenon. Students’ reflections concerned both their direct awareness, looking at and solving the equations, but also on a meta level, reflecting on their own awareness and elaborating on what they previously said (Marton & Booth, 1997). The selection of equations from the test that each student met in the interview was chosen by the researcher during the interview, depending on how they previously solved equations, with the intent to learn as much as possible about how they experience similar equations with different numbers. The students reflected on three to seven equations, depending on their inclination to elaborate on their thinking. (The equation $0.5588=0.04\cdot \mathit{x}$ was added to the selection of equations after a few interviews, to probe some more ways of experiencing the multiplicative structure).

The conversation of the interviews and the students’ writings was recorded with a video camera. The last three interviews were performed digitally, due to a pandemic. As all students where at least 15 years of age, no parental approval was requested (The Swedish Research Council, 2017). However, the students were informed of the purpose of the study and that they at any time could withdraw their participation. As anticipated, no sensitive data was registered during the interviews. All 23 interviews were transcribed verbatim. Translation of quotes was only made in the final editing of the paper and aimed at being true to the initial meaning. All the students have been given male pseudonyms when reporting the results.

Analysis

Primarily, in the analysis of the test results quantitative methods were used to display the influence of numbers on students’ ability to solve linear equations, both with descriptive statistics and by significance testing. In addition, a qualitative search for reasons behind a changed way of experiencing the same structure was also made. Initially, to minimize potential errors in the result due to how the written test was corrected, two complete corrections were performed. The tests were marked as right (1) or wrong (0), where the first correction interpreted results as right if the correct answer was mentioned anywhere in the calculations (not necessarily as the student’s answer to the equation), whereas the other correction required a correct given answer. Once the results had been shown to be independent of which of these two corrections was used, the second correction was chosen as the one to analyze further and this is the correction displayed in the findings. The frequencies of correct answers, confidence intervals and significance tests were performed in SPSS. For the significance testing the problem of multiple comparison was considered (Rice, 2007), as all equations were compared with one natural number equation. When a student had solved the equation with natural numbers, $819=39\cdot \mathit{x}$, but not a similar equation with other numbers (e.g., $0.12=0.4\cdot \mathit{x}$), the difficulties displayed by the students were analyzed. Putative reasons displayed in the erroneous solutions as the main cause of why the solution was incorrect, were gathered in a list and then summarized into six distinct categories. For example, when a student had solved $0.12=0.4\cdot \mathit{x}$ as $\mathit{x}=\frac{12}{4}=3$, it was categorized as Natural number bias as the error occurred as a cause of the preference to solve the equation with natural numbers.

The unit of analysis in the interviews was the way the students handled the equations while solving them, informed by their verbal comments. This is in line with the phenomenographic viewpoint that students’ actions are based on what they perceive (Marton, 2014). All the interview data were considered as a pool of meanings, with material that belongs both to the collective and the individual. Therefore, data should be viewed from both perspectives (Marton & Booth, 1997).

Initially, a few interviews were selected for repeated reading and analysis, with the aim to find what aspects that make students see the equations in different ways when the coefficients are from different number domains. The researcher examined several aspects of the phenomenon one at a time, looking for variation in how that specific aspect was experienced, while temporarily ignoring other dimensions. The aspects that were analyzed were not decided on beforehand but were inspired by the empirical data (the aspects that seemed to vary based on students’ utterances), or from earlier research (what has been critical for others). For example, how students spoke of coefficients – as either representing a specific number or as a general number – varied in the empirical data. Another aspect that was considered as potentially critical, with respect to earlier research, was how the equality of the equations was described by students, as a structure or as a procedure. However, when reviewing the data, neither of these dimensions explained the influence that different number domains had on students’ equation solving. First when the aspects of the meanings ascribed to the equations (semantic or syntactic) and the focus of the students was considered, the impact of a new number domain was accounted for. The data was then reviewed again concerning these dimensions and five consistent ways of experiencing the equations were formed: the dimension of meaning gave three categories (no meaning, semantic or syntactic) and two of these were split into separate conceptions depending on whether numbers was in focus or not. The categorization and main analysis were done by one researcher (the author) but has been reviewed and revised in repeated discussions with three senior colleagues and presented to other researchers in several seminars.

Results

In this section, the influence of numbers on students’ equation solving is first addressed by displaying the results of the test. Thereafter, the ways in which students experience the equations, based on the analysis of the interviews, follow.

Students’ ability to solve linear equations

Table 2 shows the success rates of the students concerning equations in the test, sorted horizontally according to structure. Looking at the frequency of correct answers for the equations with natural numbers, we can see that most students can solve some linear equations.

Table 2. Comparison of solution rates for different equations.

Structure	Equation 1 $\mathit{a},\mathit{b},\mathit{c}\in {\mathbb{Z}}^{+}$	Correct (%) (95% CI)	Equation 2 $\mathit{a},\mathit{b},\mathit{c}\in \mathbb{Q}$	Correct (%) (95% CI)	p * value
$\mathit{a}=\mathit{b}\cdot \mathit{x}$	$819=39\cdot \mathit{x}$	89.1 (83.2-95.0)	$0.12=0.4\cdot \mathit{x}$	69.1 (60.4–77.8)	<0.001
			$0.657=0.045\cdot \mathit{x}$	78.7 (71.0–86.4)	0.006
			$-24=6\cdot \mathit{x}$	74.5 (66.4–82.7)	<0.001
$\mathit{a}=\mathit{b}+\mathit{x}$	$352=63+\mathit{x}$	90.9 (85.5–96.3)	$2.01=0.434+\mathit{x}$	83.6 (76.7–90.6)	0.011
$\mathit{a}=\mathit{b}\cdot \mathit{x}+\mathbf{c}$	$37=7\cdot \mathit{x}+2$	89.1 (83.2–95.0)	$2.5=0.8\cdot \mathit{x}+2.1$	52.7 (43.4–62.1)	<0.001

*p values concerning the hypotheses H₀: p₁= p₂ and the alternative hypothesis H₁: p₁>p₂ where p₁ is the probability for a student to solve Equation 1 but not the corresponding Equation 2, and p₂ is the probability of a student to solve Equation 2 but not Equation 1. McNemar test was used, binominal distribution and exact significance (1-sided).

For all three structures, there is a decrease in success when exchanging the natural numbers in the equations for numbers with decimals or negatives, even though students had calculator aid. For each row in Table 2, the number of students that solved Equation 1 but not Equation 2, was compared to the number of students that solved Equation 2 but not Equation 1 by a McNemar test. From the low p-values we can conclude that the distribution of these two groups is not symmetrical in any row. Thereby one can conclude that there is a significant difference between the probability that a student solves an equation with natural numbers, compared to the probability of a student solving an equation with other numbers. However, comparing the probabilities of solving equations with similar kinds of numbers, such as comparing $42=3\cdot \mathit{x}$ and $819=39\cdot \mathit{x}$, respectively comparing the probabilities to solve $0.12=0.4\cdot \mathit{x}$ and $0.657=0.045\cdot \mathit{x}$, the difference was not significant (p = .254 respectively p = .132).

To learn more about why some students do not approach similar equations in the same way, the erroneous answers of students that solved $819=39\cdot \mathit{x}$, but not $-24=6\cdot \mathit{x}$, $0.12=0.4\cdot \mathit{x}$ or $0.657=0.045\cdot \mathit{x}$, have been categorized. Three of the putative reasons displayed in Figure 1, why students did not solve a similar multiplicative equation, are students’ natural number bias, usage of a wrong operation and that there was an error in the calculation. The categories in Figure 1 reveal some of the difficulties

Figure 1. Categorization of the wrong answer, 43 students in total.

* 3 of the 8 students (concerning $-24=6\cdot \mathit{x}$) use division to solve some other multiplicative equation on the test. The same accounts for 3 of the 7 students (for $0.12=0.4\cdot \mathit{x}$), and 4 of the 10 students (for $0.657=0.045\cdot \mathit{x}$).

that a new set of numbers brings to the equation. We can note that natural number bias is more frequent for the equation including numbers with decimals with few digits ($0.12=0.4\cdot \mathit{x}$). This is also an explanation why this equation has a lower solution frequency in Table 1, than similar multiplicative equations. Another notion seen in Figure 1 is that mistaking multiplication for another operation seems to occur for all equations (there were also students who solved $0.12=0.4\cdot \mathit{x}$ respectively $0.657=0.045\cdot \mathit{x}$, but used addition or subtraction for $819=39\cdot \mathit{x}$).

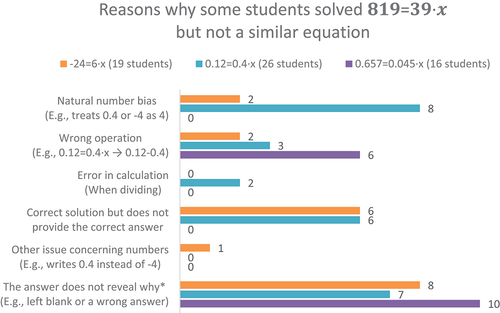
Several answers did not reveal why the students solved one equation but not the other (the last category). However, if a student does not use a systematic algorithm, such as division, to solve a multiplicative equation with natural numbers (e.g., $819=39\cdot \mathit{x}$), it is not surprising that the student is less likely to solve a similar equation with numbers with decimals (e.g., $0.657=0.045\cdot \mathit{x}$) – as calculating the latter without division usually include more steps. This was not possible to control for, as students did not always explain their answers in the test, which is why it is impossible to say how many students that did have a general solution method such as division but did not use it.

It is however interesting to see that students who show their use of division did not always apply the same solution method for multiplicative equations with other numbers. An example of this is given in Figure 2, where a student seems to experience seven multiplicative equations – the last equation being multiplicative first after transformation – in (at least) three different ways: as something to divide, as something unfamiliar and as solvable using percentage. However, we cannot say from this test how the student truly comprehends these equations. This is instead addressed when the results from the interviews are analyzed.

Figure 2. One student’s answers from the same occasion (Glenn).

Students’ ways of experiencing the solving of linear equations

From the phenomenographic analysis of the 23 student interviews, five different ways of experiencing linear equations (A – E) emerged. Three of these describe ways of experiencing the equations as meaningful and displaying a structure; (A) a relation between operations and elements, (B) a relation between numbers and (C) a relation that must represent a situation. The other two, (D) numbers to compute and (E) an unfamiliar equation, describe ways of experiencing where the meaning of the equation is not fully discerned.

The two essential dimensions, which were found to cause the varying influence of the nature of numbers were, first: what aspect of the equation was seen in the foreground (operations, numbers or structure), and second: whether the equation was seen as carrying meaning, semantically or syntactically. These two dimensions in the conceptions are thereby also what makes the categories distinct and variation in these explains how they are logically related. The empirical examples display how the nature of numbers has the greatest influence in conception E and least in conception A.

The five ways of experiencing linear equations were found in the interview data. The descriptions pertain to the students’ experience of solving the equations, based on how they justify their solution process. First, each conception is described in general, followed by examples from the data, and finally displayed in an outcome space (Table 3).

Table 3. Outcome space of the conceptions.

The linear equation is experienced as …	Meaning discerned in the structure	Aspect in foreground
A. … a relation between operations and elements	Syntactic meaning	Structure
B. … a relation between numbers	Syntactic meaning	Numbers and structure
C. … a relation that must represent a situation	Semantic meaning	Numbers and structure
D. … numbers to compute	Searches for a meaning	Operation
E. … an unfamiliar equation	Searches for a meaning	Numbers

E. An unfamiliar equation

Experiencing an equation as unfamiliar is characterized by a search for meaning in the equation, with a focus on the numbers. A semantic or syntactic meaning is required to solve the equation but is here limited by the experience of the numbers in the equation as foreign or unsuitable. A typical example of this way of experiencing is when someone is stuck – not solving an equation like $2.5=0.8\cdot \mathrm{x}+2.1$ – and searches for a meaning in the numbers: pondering what rules apply to this specific kind of numbers or what the numbers can represent to make it more understandable. Three examples from the data display this way of experiencing.

The first example is from an interview with Fredrik who (after solving $0.12=0.4\cdot \mathrm{x}$ by transforming it to natural numbers and later $42=3\cdot \mathrm{x}$ by division on the calculator), does not think of a solution for $0.657=0.045\cdot \mathit{x}$. The numbers are explained as the cause of the equation being experienced as unfamiliar: “Yes, that’s it. There is another zero there [in 0,045]. Yes, now it spoiled things. I don’t know actually.” He does not discern a meaning in the equations as he does not know how to handle the numbers. The multiplicative similarity between the equations is experienced in the background, and the focus is on the numbers.

The second example from this way of experiencing is when the numbers do not fit into the intended interpretation of the equation. In an interview with Emil, he describes dividing with three, in the equation $42=3\cdot \mathrm{x}$, as “removing” 3 (i.e., when you share things, the multiplication is reversed). This way of seeing structure is not applicable for him to the equation 0.12 = 0.4 ∙ x: “I don’t know if I can divide 0.4 with 0.4 because I want to remove 0.4. […] For when I typed ‘0.4 divided with 0.4,’ then it is one.” In this way he searches for meaning to see structure and the numbers are in focus in the search.

Thirdly, the focus on numbers can result in the operation being completely “overlooked.” An example is given by Filip, who is set on trying to solve $0.12=0.4\cdot \mathit{x}$ with the strategy of “getting the x alone” on one side by subtraction:

F: Since it’s plus there [points at 0.4]

I: Yes, right.

F: There are no minus numbers.

I: That’s right, and where is the plus? [Filip points at 0.4]

F: So, there are no minus numbers.

As 0.4 and its sign are in the foreground of Filip’s attention, the multiplication sign is not distinguished, and neither is the structure. Several examples of experiencing in this way show that when the numbers are in the foreground in the search for meaning, the operation is sometimes not noticed until another equation, or a question of clarification directs the attention to the operation. In the case of Filip, it is a similar equation with natural numbers, $42=3\cdot \mathit{x}$, that directs his attention to the operation and to what method gives a reasonable answer, which he later can apply to the equation with decimal numbers.

D. Numbers to compute

Just as in conception E, structure is not discerned when experiencing the equation as Numbers to compute. However, the focus is on the operations (not the numbers as in conception E) in the search for meaning (semantic or syntactic). The operation is seen as the key to a solution method that should produce a correct answer, without knowledge of why. Typical to this way of experiencing would be to see $2.5=0.8\cdot \mathrm{x}+2.1$ without a clear meaning, but with a focus on the operations – pondering in what order to perform possible operations like dividing 0.8 or subtracting 2.1, or what are the correct inverse operations to multiplication and addition. The following three examples from the data display this way of experiencing.

The first example is from an interview with Gunnar (who just solved $0.12=0.4\cdot \mathit{x}$ with division, as he recognized that $4\cdot 3=12$) but addressing $0.657=0.045\cdot \mathit{x}$ he divides $0.045$ with $\mathrm{0.657.}$ He explains: “I don’t know really, but I took 0.045 divided with 0.657, since it was on the same side as x, if you should remove all numbers from x.” This shows that he has discerned the operation, but the syntactic meaning of the equation is not clear to him – how and why the numbers would be arranged in a certain way. In this way, the numbers influence, even though they are not in focus, as more unfamiliar numbers do not assist the students to see meaning.

A similar example is given by Anders:

I: And when you do this, you speak of multiplication and division as connected. How do you know which one to divide with which?

A: So, the whole, divided with the share, or that sort of thing.

I: Yes, right. Here [$0.12=0.4\cdot \mathit{x}$] you took 0.12 divided with 0.4. And here [$0.657=0.045\cdot \mathit{x}$] you took 0.045 divided with 0.657. How do you know it’s not the other way around?

A: I don’t know.

I: No?

A: The least up there and the greatest down there.

Anders does not see the structure, but he knows the equation should be solved with division. In the search for a meaning, he tries to apply explanations as “the whole, divided with the share,” and “the least up there and the greatest down there,” without reaching a satisfying meaning of how the numbers are related.

Thirdly, Erik also experiences the equation $0.588=0.4\cdot \mathit{x}$ in this way as he explains why he used division as he “tried some different things and it worked.” As the solution occurred without a clear meaning, the structure was not discerned while solving the equation. However, “checking the answer” gives some meaning to the equation after it has been solved.

C. A relation that must represent a situation

The main characteristic in experiencing the equation as a relation that must represent a situation is the need to see its meaning as semantic, that the equation requires a real-world interpretation to be handled. The focus is both on the numbers – as they have to correspond to the situation being represented – and the structure. In contrast to conception E and D, a structure is here discerned as the equation is given a clear meaning. Typical for this conception would be to regard $2.5=0.8\cdot \mathrm{x}+2.1$ as representing a concrete situation, for example, distributing two and a half liters of water in different bottles or putting a number of objects on a scale to make it balance – semantic meanings that only fit certain kinds of numbers. The following four examples from the data illustrate this way of experiencing.

The first example is from an interview with Elias that describes $-24=6\cdot \mathit{x}$ as “if I had a debt of four kronor [the Swedish currency] to six people, then I owe people 24 kronor.” The number and the structure of the equation are in focus as they must fit the given context; negative numbers remind him of loaning money and division of fitting a content into another.

Numbers can also preclude the semantic meaning that the equation otherwise would be interpreted with. Returning to an earlier section of the interview with Emil, he searches for a meaning in $0.12=0.4\cdot \mathrm{x}$, initially addressing it with subtraction, but discerns the multiplication sign in $42=3\cdot \mathit{x}$ as representing a number of things:

I: Let’s take another here [shows $42=3\cdot \mathit{x}$]

E: Mhm

I: What are you thinking now?

E: I did the other one wrong [$0.12=0.4\cdot \mathit{x}$] I also noticed.

I: Mhm.

E: For now I remembered something, or no. What I learnt last year in school was that when it says “three times x” then it is three x:es. And then you can take three x divided by three to remove the three. Then you do the same thing on the other side and then you find what x is.

In this way, Emil sees structure in the equation $42=3\cdot \mathit{x}$ as representing a concrete situation where the numbers and structure can be visualized as three things that together make 42. The same meaning is not seen in $0.12=0.4\cdot \mathit{x}$ and when returning to this equation with numbers with decimals, division still does not make sense as division – as previously mentioned – is understood as dividing a number of things, which “removes” the coefficient in front of x, but dividing 0.4 things is not as easy to visualize.

The last two examples are related to this, the interpretation of division as handling a content. Glenn describes $819=39\cdot \mathit{x}$ as: “There are 39 shares and of these 39 shares, one part consists of a quantity of x […] then you just divide 819 with 39 and then you get x.” In this way, the structure can be concretely visualized, where the numbers and the structure have clear referents in the picture. However, when the numbers do not fit that structure, another interpretation is needed. This is exemplified as Elias elaborates on his experience of division as fitting a content into another:

I: Here [$819=39\cdot \mathit{x}$ and $0.657=0.045\cdot \mathit{x}]$ you divided. Would it be possible to do that here also? [points at $0.12=0.4\cdot \mathit{x}$ and $-24=\mathit{x}\cdot 6$]

E: I don’t know. Maybe. It is harder for me when it is like 0.12 there and then 0.4 times x. Then that is like the bigger [points at 0.4].

Elias sees the same concrete structure in the first two equations, they are examples of how a number of things can be put into a larger number of things. When the dividend is less than the divisor, the same meaning cannot be applied, and structure is not discerned. Returning to Glenn, who did not answer $0.657=0.045\cdot \mathit{x}$ in the test (see Figure 2) (presumably because he did not see meaning in the equation), in the interview comes to think of it as resembling percentage, in terms of part and whole, and is then able to solve the equation. We can therefore hypothesize that the need to search for a situation to symbolize the equation can limit students’ possibilities to recognize familiar structures.

B. A relation between numbers

Experiencing the equation as a relation between numbers is based on discerning the meaning of the equation as syntactic. In contrast to conception C, where the equation needs to refer to a concrete situation, this way of experiencing equations does not involve a real-world reference. Numbers and symbols are instead seen as a structure by their syntactic meaning, describing connections that build on mathematical properties and rules. Still, the numbers and the structure are in the foreground. The numerical focus can be observed when students concentrate on handling the numbers: factorizing, transforming numbers, and using known number facts such as multiplication tables. Typical to this conception would be to regard $2.5=0.8\cdot \mathrm{x}+2.1$ without thinking of concrete referents – but rather how the expression can be handled theoretically, for example, the numbers can be transformed into $25=8\cdot \mathit{x}+21$ and then we know eight times a half is four, which will satisfy the equation. Four examples from the data illustrate this conception.

The first example is from Bill’s experience of the equation $0.12=0.4\cdot \mathit{x}$:

Then I often think that, instead of making this a decimal fraction I think in my head that it is like 12 equals 4 ×. And then I always do division, 12 through four which is three, yes three. So, x equals three and then I usually double check so that I always take four times three equals 12. Which is the answer.

Bill sees structure syntactically, as he is set on transforming the numbers and does not refer to what they represent. He focuses on the numbers, helped by the familiar number combination $4\cdot 3=12$. However, as he does not convert 3 back to 0.3 it implies that the numbers not only catch his attention but that the relation between natural numbers and decimal numbers is not clear to him, which is also the case later in the interview. Bill reflects that it is easier to use the number fact $4\cdot 3=12$ in this case to see the solution, whilst division has to be used when the coefficients have many digits.

The second example is another from the interview with Fredrik. In the interview, he showed that he could solve $42=3\cdot \mathit{x}$ by division on the calculator. However, in both the test and the interview, he solved $0.12=0.4\cdot \mathit{x}$ by transforming the numbers to natural numbers and in the test, he even wrote, “do not think in decimal form.” In the interview, he is explicitly asked if it would be possible to use division for $0.12=0.4\cdot \mathit{x}$ or $0.657=0.045\cdot \mathit{x}$. He is open to testing the suggestion, but as he wants to verify this on the calculator, he dials a digit wrong and remains uncertain until he later in the interview can conclude that the method works for the latter equation. As Fredrik is focused on the form of the numbers, rather than what they represent, the equation $0.12=0.4\cdot \mathit{x}$ is seen as carrying syntactic meaning. The numbers are experienced in the foreground as they guide his choice of method.

A similar example is from an interview with David, who is asked if it would be possible to use division straight away for the equation $0.12=0.4\cdot \mathrm{x}$, without having to convert it to natural numbers first (as he just had done):

D: Eh, [takes up the calculator and taps it] yes, you can.

I: Yes.

D: I thought that it would become even less for some reason but… […] that’s right, when you divide something, it does not become much less. It is when it is lower than one that it does not become, yes, there is also some rule like that when you multiply something less than one.

Contemplating the rules for what operations that are allowed, the structure is seen as carrying syntactic meaning. In this way, the numbers (and the structure) are in focus, and influence what solution path is chosen.

The last example is from Elliot who address $0.657=0.045\cdot \mathit{x}$ by dividing both sides of the equation with 0.045. He explains that the coefficient on the right hand side is canceled, and the answer is 14.6. He finishes by saying a bit hesitant, “yes, I think that should be correct, division with zero comma something, then the number gets bigger, so then it feels right.” Also, here, structure is seen because Elliot has knowledge of the rules of the mathematical system, the syntax, and that he is allowed to cancel symbols if a coefficient is divided by itself. The numerical focus is also here explicitly stated.

A. A relation between operations and elements

Experiencing linear equations in this way, the structure is – just as in conception B – given a syntactic meaning. However, the numbers are now in the background – being overlooked – not influencing the solution path to a large extent. Instead, the focus is on the structure and how the numbers and operations are connected. Typical to this conception is to see any equation with the same structure as the same, for example, experiencing $2.5=0.8\cdot \mathrm{x}+2.1\mathit{\hspace{0.17em}}$ in the same way as $37=7\cdot \mathrm{x}+2$. The relations between the elements of the equation (the numbers and variables) are in focus and a solution is formed by arranging the positions of these. Examples from two students display this way of experiencing.

It is natural to use the names of numbers when solving an equation, also in this way of experiencing. However, the emphasis when speaking of numbers is rather on their positions than their values, just as it is for Gunnar when he elaborates on his solution for the equation $0.12=0.4\cdot \mathit{x}$:

Eh, I think since we want to move over the x, since we only should have x on one side, I think that one instead of moving all – instead of moving twelve to the right, over there to one side and then moving the x there – then one would have got the right answer anyway. But then I think it is easier to just move 0.4 over.

The structure is here seen as carrying syntactic meaning as Gunnar refers to possible symbolic maneuvers. Numbers and variables are only referred to as elements of the equation that can be arranged in different ways. Numerical values are seen in the background and do not guide the solution. Sometimes the numbers are not even mentioned, as when Edvard addresses $2.01=0.434+\mathit{x}$: “I took the difference. Yes, but the difference between those numbers is that number.” The structure to Edvard is here described as a relation between unspecified numbers. In this way, issues concerning numbers, such as what numbers are allowed or their proportions, do not have a great influence on the equation solving.

Table 3 displays how this way of experiencing is logically related to the other conceptions. The most refined way of experiencing is presented at the top of the table. For each conception it is also listed what meaning is seen in the equation and what aspect of the equation that is experienced in the foreground.

Discussion

Initially, this study set out to give a comprehensive overview of how the nature of numbers used as coefficients influences how students see equations in the process of solving them. The reason for this aspiration is to further explore numbers as a potential difficulty in algebra, an aspect that is not often emphasized in research, and to discuss possible ways to develop teaching.

First, we wanted to learn how students’ ability to solve equations is affected when coefficients are from different number domains. For teachers and mathematicians, equations of a certain structure usually appear similar, with the same possible solution methods (especially with a calculator). However, the result of the test in this study shows that the probabilities for a student to solve equations of the same structure, but with coefficients from different number domains are not necessarily the same. We registered a decrease in students’ ability to solve equations of identical structure when coefficients are negative integers or numbers with decimals, compared to natural numbers, despite students having calculator aid. This confirms findings from earlier research on equations with negative numbers (Vlassis, 2008).

Looking at the result from the test, we can also see that numbers within the same domain of numbers can bring different challenges for students. This can be seen as 8 of the 26 students that solve $819=39\cdot \mathit{x}$ but fail to solve $0.12=0.4\cdot \mathit{x}$ do so because they see that four times three is twelve, and wrongly conclude that three is the correct answer. The same biasing number combination is not offered by the equation $0.657=0.045\cdot \mathit{x}$, even though these coefficients also are numbers with decimals.

The results also confirm that, for some types of numbers, the multiplicative relation is more difficult to recognize, compared to the additive relations (Vlassis, 2008). Overall, we can conclude that the students’ ability to solve equations is affected by the choice of coefficients. However, Figure 1 shows that the answers of several students did not explain why they could solve the equation with positive integers, but not a similar one with other numbers, wherefore further qualitative investigation was motivated.

Therefore, secondly, we also set out to explore the ways students experience equations when the coefficients are from different number domains. When analyzing how students experienced the equations, two dimensions were found to explain how the nature of numbers influenced the way of experiencing – the meaning seen in the equations (semantic or syntactic), and what aspect of the equation was focused on by the student. Comparing the conceptions with previous research, we can see that Conception C (a relation that must represent a situation) has been presented before, and the abstract nature of numbers has been put forth as a reason why students experiencing in this way do not solve equations of similar structure (Vlassis, 2002). This study gives new evidence for this and adds to the description that numbers’ influence varies by how well they fit into a student’s interpretation of a situation (e.g., the possibility for an expression to represent a discrete number of things) and that the numbers guide what contexts that the students come to think of for an equation (like Glenn in Figure 2). Further on, conception B (a relation between numbers) describes the experience of equation solving as relying on the equation as a syntactic construction with the numbers in the foreground. Also here, previous experience of numbers concerning syntax, for example, biasing number combinations (Linchevski & Livneh, 1999) or perceived rules concerning the range of numbers allowed (Christou & Vosniadou, 2012; Christou et al., 2022), interfere with students’ ability to see structure.

Summarizing the reasons for students’ difficulties to see structure in presence of certain numbers, two answers have been generated. First of all, in both Conception C and Conception B, some students have not yet generalized the properties of the equations to apply to equations with coefficients from different number domains. From the examples we can see that staying in the local context (with the concrete situations or the natural numbers) limits the experience of the structure, for example, the ability to see the solution of $42=3\cdot \mathit{x}$, not only as splitting 42 into three groups, but as dividing both sides with three to produce the multiplicative inverse: one. This is in line with Venkat et al. (2019) as they mean that generalization is required to discern mathematical structure. Secondly, some students direct their focus to numbers, where it – in this algebraic situation – would be more beneficial to look at the operations and relations in the equation to see structure. In these cases, it is not the numbers as underlying context that is difficult, but the ability to “see through” the numbers to see structure (Kieran, 2018) and looking at the form of expressions rather their values when computed (Kaput, 2008). This suggests that the ability to see numbers in the background of equations is not only hindered by isolated (mis)conceptions concerning a certain type of numbers but relates to how the whole equation is experienced.

The contribution of this study is not primarily the isolated experiences described in the categorizations, but their combination in a framework that displays how numbers are given varying attention depending on how students experience an equation. The results describe how the numbers affect the whole process of students’ equation solving; starting by impacting what the students notice, then influencing on a deeper level what meaning-making the students choose for the equation and finally, which answer that is considered reliable. It is also noteworthy that depending on what meaning the student sees in the equation, the same type of number can encourage different mathematical thinking. For one student, the numbers in the equation $0.657=0.045\cdot \mathit{x}$ made it more difficult to see structure (see Figure 2), as it was difficult to find a context in which the equation can be given meaning. Whereas for another student the same numbers made it easier to see structure as it is possible to fit $0.045$ into $0.657$, which is not always the situation. On several occasions, numbers with few digits encouraged students to compare the equation with a similar equation but with natural numbers (e.g., $0.12=0.4\cdot \mathit{x}$ with $12=4\cdot \mathit{x}$). This suggests that the choice of numbers can be used to induce different ways of thinking, depending on what features students notice and what structural aspects those features emphasize (cf. English & Sharry, 1996).

How a wider range of numbers can be used in algebraic teaching to put structure in the foreground is an interesting topic for further research. The use of large numbers has previously been suggested as a way of foregrounding structure and perceiving the numbers in the background (Kieran, 2018; Zazkis, 2001). The use of “unusual” numbers as coefficients (such as $2.67x^2-3.86\mathit{x}-12.23=0$) can display the irrelevance of numerical values in equations (Greer, 2006). The use of calculators can help to mediate the idea that numbers are equally possible to calculate (Kieran, 2018; Warren, 2003). Furthermore, the topics raised in this article, (1) how the numerical context of the equations are essential for generalizing, and (2) how students should focus on the relations in equations to foreground structure, could be beneficial for teachers to consider in teaching to make students less influenced by numbers in their equation solving. Another educational implication for teachers is to consider that students equation solving skills cannot be evaluated by how they solve one equation, as students’ difficulties might not be algebraic, but related to certain numbers.

To conclude, the results show that students in the process of learning to solve equations are influenced by previous experiences of numbers to a varying degree, depending on the meaning they give to the equation and what aspects of the equations are in their focus. Numbers should, therefore, not be considered in isolation, as prerequisites just influencing the computation, but rather as symbols that students should learn to interpret in an algebraic way – the algebraic way of thinking that Viète described when symbolizing coefficients with letters. This way of thinking will be relevant, not least to students in vocational education focusing on electricity, as they will need to be able to handle equations with a wide range of numbers in their profession.

Since the results in this study are based on a specific group of students there are limitations to consider. For the test, choosing a randomized sample from a larger group of vocational students would give further results on how students handle structures of similar equations. Furthermore, performing the test in other countries where teaching is different, it is possible that students manage these equations differently. Reflecting on the limitations of the interviews, it is interesting to consider if there would be other ways of experiencing the equations in other student groups than the vocational and where students are of another age. However, it is reasonable to think that all students learning equation solving need to consider the role of numbers at some point and that the results of this study could still be relevant in other student groups. Considering the limitations of this study, and the possibilities for further research, it is also essential to consider the sample of equations and the use of other numbers as coefficients, for example, other properties (larger or smaller), different ratios between the coefficients or on other forms (like fractions). These are a few things that remain to be further explored.

Acknowledgments

This research is part of a PhD-project within the graduate school in educational science at the Centre for Educational Science and Teacher Research (CUL) at The University of Gothenburg.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Notes on contributors

Anna Holmlund

Anna Holmlund is a PhD-student at The University of Gothenburg and Chalmers University of Technology, with a background as a mathematics and physics teacher in upper secondary school. Her research interest concerns how students experience learning objectives in algebra and how this can be used to promote teaching.