Advanced search
Publication Cover
Astronomical Review Volume 12, 2016 - Issue 1-4
Journal homepage
2,128
Views
15
CrossRef citations to date
0
Altmetric
Review Articles

Formation of exomoons: a solar system perspective

Amy C. BarrPlanetary Science Institute, Tucson, AZ, USA.Correspondence[email protected]
Pages 24-52 | Received 15 Sep 2016, Accepted 03 Jan 2017, Published online: 23 Jan 2017

Figures & data

Table 1. Properties of the major satellites in our solar system and their modes of origin.

Figure 1. Satellites of our Solar System’s planets (dots), as a function of satellite-to-planet mass ratio (left), and ratio of total angular momentum in the orbital motion of the satellites, to the total system angular momentum, [Citation147].

Note: Satellites thought to have formed from a giant impact, Earth’s Moon, and Pluto’s satellite Charon, are shown as open circles.
Figure 1. Satellites of our Solar System’s planets (dots), as a function of satellite-to-planet mass ratio (left), and ratio of total angular momentum in the orbital motion of the satellites, to the total system angular momentum, [Citation147].

Figure 2. CTH simulation of the Moon-forming impact, after Canup et al. (2013) [Citation76]; details about the simulation method, equations of state, and data analysis may be found in this reference.

Notes: A Mars-sized object composed of 70% rock and 30% iron collides with the protoearth of similar bulk composition, with a impact angle, at . Colors indicate density in g/cm, on a logarithmic scale. Simulation results are plotted as a function of time for (a), 1 (b), 1.8 (c), 3.4 (d), 4.8 (e), and 10 h (f) after the impact. The impact launches a disk of lunar masses worth of silicate-rich material into orbit.
Figure 2. CTH simulation of the Moon-forming impact, after Canup et al. (2013) [Citation76]; details about the simulation method, equations of state, and data analysis may be found in this reference.

Figure 3. Reproduced with permission from Kokubo et al. (2000) [Citation78]. Time-evolution of a gas-free disk of debris after the Moon-forming impact (simulation 15a). Four lunar masses of material is initially distributed in a region 2 Roche radii from the Earth (about 6 Earth radii).

Notes: The particles obey a size distribution , where n is the number of particles, and m is particle mass. If the particles all of equal mass, they would have a radius km, assuming a density of 3.3 g/cm for the disk material. Time is reported in units of the orbital period at the Roche limit,  h for the Earth. Over the entire duration of the simulation, 1000 (or 290 days, where 1 day is 24 h), a single large Moon accretes just outside the Roche limit.
Figure 3. Reproduced with permission from Kokubo et al. (2000) [Citation78]. Time-evolution of a gas-free disk of debris after the Moon-forming impact (simulation 15a). Four lunar masses of material is initially distributed in a region 2 Roche radii from the Earth (about 6 Earth radii).

Figure 4. Reproduced, with permission from Figure of [Citation68]. Snapshots of the gas-free accretion of solid debris after an impact between two rock/metal planets. The disk initially contains 1.25 lunar masses of material, with specific angular momentum . Results are shown looking down onto the disk from above.

Notes: The disk material is initially distributed between 0.4 and 1 Roche radius from the planet, which has a radius 0.34 Roche radii ( Earth radius). Numbers indicate elapsed time in units of the orbital period at the Roche limit, which for Earth, is about 7 h.
Figure 4. Reproduced, with permission from Figure 5 of [Citation68]. Snapshots of the gas-free accretion of solid debris after an impact between two rock/metal planets. The disk initially contains 1.25 lunar masses of material, with specific angular momentum . Results are shown looking down onto the disk from above.

Figure 5. Reproduced with permission from Canup (2005) [Citation17]. Time-evolution of a smoothed particle hydrodynamics simulation of a potential Pluto-Charon-forming impact between two pure serpentine objects (run20 in Table 1 of Canup (2005)).

Notes: The results are shown at times (A) , (B) 3.2, (C) 5.9, (D) 7.5, (E) 11.2, and (F) 27.5 h. Colors indicate the change in temperature from the initial condition, with red indicating 250 K, and blue indicating no temperature change. Distances are shown in units of km. The objects collide with an angle of 73, at . The final state is a single intact moon with .
Figure 5. Reproduced with permission from Canup (2005) [Citation17]. Time-evolution of a smoothed particle hydrodynamics simulation of a potential Pluto-Charon-forming impact between two pure serpentine objects (run20 in Table 1 of Canup (2005)).

Figure 6. Reproduced, with permission from Figure of Tanigawa et al. (2012) [Citation107]. (left) Colors indicate values of the potential relative to Lagrange points L and L.

Notes: The streamline starting from ( for a Jupiter-mass planet) indicates particle trajectories in the midplane of a circumplanetary disk. Dimensions are scaled by planetary Hill radii. (right) Same as left panel, showing particle streamlines originating at , (), and ().
Figure 6. Reproduced, with permission from Figure 2 of Tanigawa et al. (2012) [Citation107]. (left) Colors indicate values of the potential relative to Lagrange points L and L.

Figure 7. Schematic of the gas-starved disk, based on models of Canup & Ward (2002, 2006) [Citation27,Citation30]. Ice/rock particles + gas from the solar nebula deliver mass to .

Notes: Gas spreads beyond and on to the planet. Solids in the midplane grow large enough to de-couple from gas, build up in the midplane and accrete into satellites. Satellite growth times and disk temperatures are controlled by the inflow rate.
Figure 7. Schematic of the gas-starved disk, based on models of Canup & Ward (2002, 2006) [Citation27,Citation30]. Ice/rock particles + gas from the solar nebula deliver mass to .

Figure 8. Schematic depicting the power of microlensing, spectroastrometric, and transit exomoon detection and characterization methods, as a function of satellite-to-planet mass ratio, and satellite semi-major axis.

Notes: Approximate location of the Solar System’s satellites are shown as dots: brown/blue dots indicate the mixed ice/rock satellites of the outer planets and Charon, the Moon is represented by a brown dot. Giant impacts have the potential to form the large required to observe exomoons via transits and spectroastrometric methods. Microlensing has the potential to observe smaller satellites. What is not depicted on this graph is the difficulty of detecting the host planet to begin with. All of our Solar System’s planets are barely detectable using present instrumentation: there is essentially no chance of detecting a dwarf planet like Pluto using any present or planned telescopes.
Figure 8. Schematic depicting the power of microlensing, spectroastrometric, and transit exomoon detection and characterization methods, as a function of satellite-to-planet mass ratio, and satellite semi-major axis.

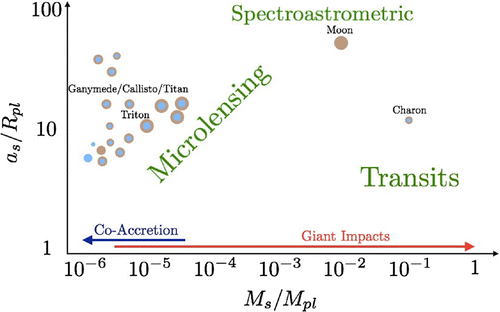
Figure 9. Reproduced, with permission, from Kipping 2014 [Citation142]. Schematic illustration of the effect of an orbiting moon on the timing and duration of planetary transits.

Notes: The center of mass of the planet/satellite system follows a Keplerian orbit around the central star (gray line), but the location of planet itself (red/blue) deviates from a Keplerian orbit (red/blue). This causes changes in the timing and duration of transits relative to those predicted for a planet alone.
Figure 9. Reproduced, with permission, from Kipping 2014 [Citation142]. Schematic illustration of the effect of an orbiting moon on the timing and duration of planetary transits.

Related research

People also read lists articles that other readers of this article have read.

Recommended articles lists articles that we recommend and is powered by our AI driven recommendation engine.

Cited by lists all citing articles based on Crossref citations.
Articles with the Crossref icon will open in a new tab.